AMC10竞赛考察哪些内容,我们整理了近十年的AMC10数学竞赛考题,发现AMC10数学竞赛考察的知识点无非就是这19个,只要吃透这些点,在25年的AMC10数学竞赛中,就可以取得好的竞赛成绩。
AMC10竞赛19个知识点AMC10竞赛几何板块知识点
1、平行线分线段成比例定理
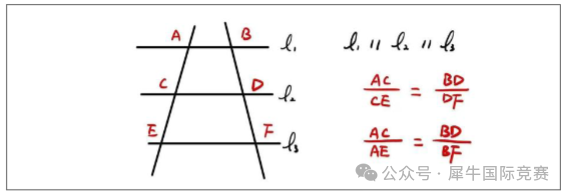
不仅仅适用于相似三角形,其核心思想是找到两到三组平行线,利用平行线分割的线段找出比例关系。
2、射影定理(Euclid'stheorem)
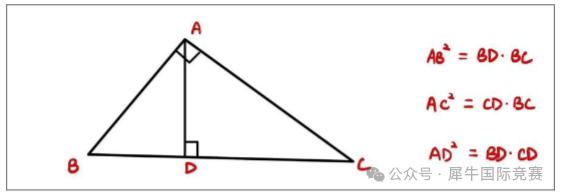
可以通过中学学习的相似三角形的知识证明。是和直角三角形相关的题目的重要解题线索,使用时,只需要找出一个直角三角形和其斜边的高,就可以对未知边长进行求解。
3、角平分线定理(Anglebisectortheorem)
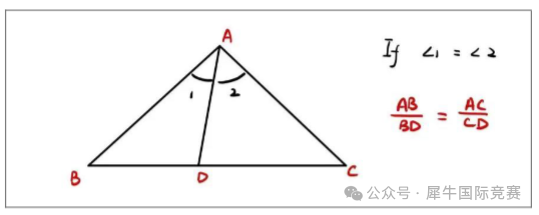
一个在AMC10的几何难题中颇为实用的定理。看到了角平分线的信息,就可以找出线段之间的比例关系。
掌握了这样一个定理,即便是AMC10的压轴题也不在话下。
4、利用正弦求三角形面积

这一结论也是针对中学三角知识的延伸,不仅仅可以求三角形的面积,还可以在已知两个三角形其中一个内角相等的前提下,找出对应边长的比例关系。
5、斯图尔特定理(Stewartstheorem)
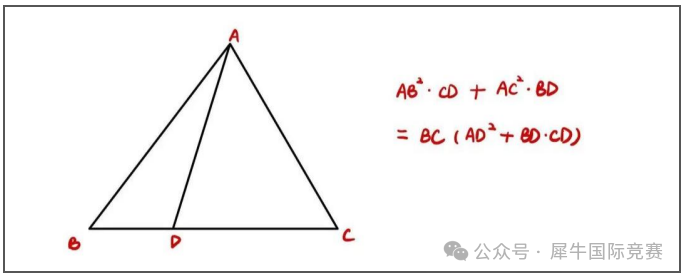
这个定理不太好记,当D点为中点时还可以简化为中线定理。作为比较不常用的定理,适合针对最后五题复习的同学。
AMC10竞赛代数板块知识点
6、韦达定理(Vieta'sFormula)

韦达定理是一个应用面非常广的定理,还可以拓展到更高阶次,描述一元n次多项式根的关系。
7、算数平均-几何平均不等式(ArithmeticMean-GeometricMeanInequality)

这个不等式是对课内所学平方和不等式的一个拓展。同时这个不等式还可以和算数平均,几何平均这两个统计学概念一起进行记忆。
8、二项式定理(BinomialTheorem)

由二次多项式拓展出的结论。掌握了二项式定理,结合杨辉三角,这个定理的结论记得更牢。
9、合分比定理(PartitionRatioTheorem)

这个定理的形式有很多种,无论是在代数,还是几何问题中,根据已知比例求比例的问题,都可以尝试用合分比定理作为解题的核心思路。
10、余数定理(PolynomialRemainderTheorem)

一个中学阶段看似普通的定理,其结论和延伸出的因式定理在处理多项式的问题时,有时有着意想不到的功效。
AMC10竞赛数论板块知识点
11、孙子定理(ChineseRemainderTheorem)

就是根据不同除数得到的余数,求解满足条件数字的问题。
12、费马小定理(Fermat'sLittleTheorem)

是一个在数论问题中频繁被使用的定理。此定理可以求解大部分和指数表达式相关的余数问题。
13、威尔逊定理(Wilson'sTheorem)
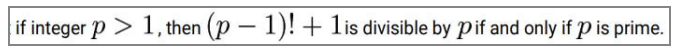
这也是在AMC10的考试中出现过的一个和求余数相关的定理。也可以用来判断一个自然数是否是质数。
14、欧几里德算法(EuclideanAlgorithm)

欧几里德算法又叫做辗转相除法,是用来计算两个整数之间最大公约数的方法。其核心思想是,两数相除得到的余数与其中任意一个数的最大公约数等于原本两个数的最大公约数。该算法的逆过程经常被用来推算一些数的最大公约数。
15、立方和公式(Nicomachus'sTheorem)
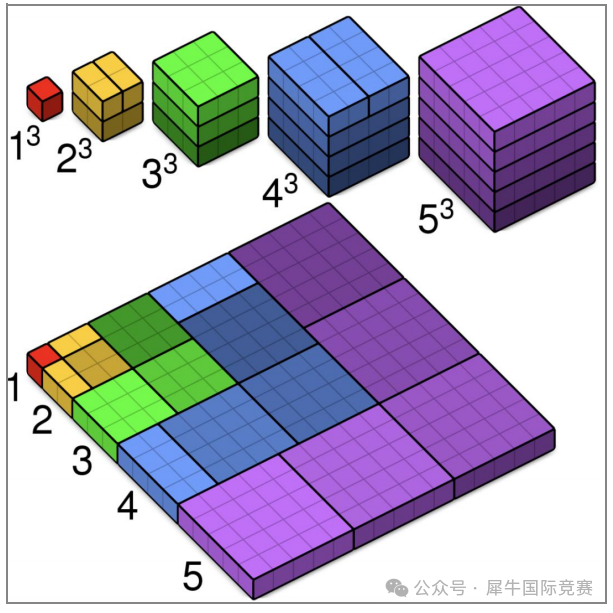
这个定理是可以被可视化证明的。从1开始的连续正整数的立方和等于对应几个正整数和的平方。虽然可以使用的机会很少,在特定题目中使用该定理,还是会大大简化求解过程。
AMC10竞赛计数板块知识点
16、互补计数(ComplementaryCounting)
互补计数就是计算所求集合中补集的元素个数。典型的例子是找出“至少有n个”的互补情况,也就是“至多有n-1”。
结合题目中出现的"至多"、“至少”这样的关键词,利用互补的思想,可以使一些计数和概率计算变得更简洁有效。
17、容斥原理(PrincipleofInclusion-Exclusion)

容斥原理是另一个计数问题中常见的集合原理。通常使用容斥原理可以计算两个或者多个不同的类别重叠部分元素的个数。它的集合表达式如下,一般来说只需要掌握两集合,三集合对应的结论就可以了。
18、可分辨性(Distinguishability)
可辨性最好的应用就是“隔板法”,关于隔板法的问题可以描述为将n个元素分为k组或者k个非负变量之和等于整数n。
19、鸽巢原理(PigeonholePrinciple)
鸽巢原理也叫抽屉原理,简单的解释为n+1个元素分成n组,至少有一组包含两个元素。又或者为什么一个学校里,一定有两个同学的生日是同一天呢?因为生日只有366种,而学校的人数一定大于366,所以一定有人的生日相同。
AMC10核心考点公式汇总
关于本次为大家展示的AMC10数学竞赛的的19个核心考点,老师已整理成册,除了考点解析外,还有历年类似考题的解析过程,让大家更清楚直观的运用这些定理。