提到数学竞赛,AMC绝对是绕不开的 “重头戏”—— 无论是想提升数学思维,还是为升学积累竞争力,它都是很多同学的首选。
但对于第一次接触AMC的同学和家长来说,最头疼的往往是:备考从什么时候开始?不同阶段该重点练什么?怎么避开低效刷题的坑?
今天这篇内容,就专门为大家拆解AMC系列赛事的备考节奏,想打好AMC这场仗,先从搞懂 “怎么准备” 开始吧!
AMC竞赛体系
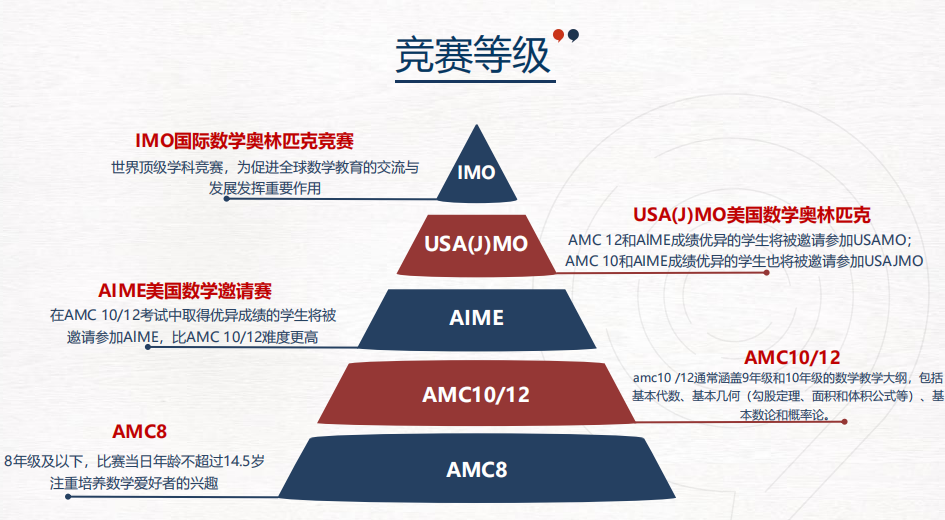
AMC数学竞赛体系覆盖从小学到高中的全年龄段学生,主要分为AMC8、AMC10、AMC12三个级别。
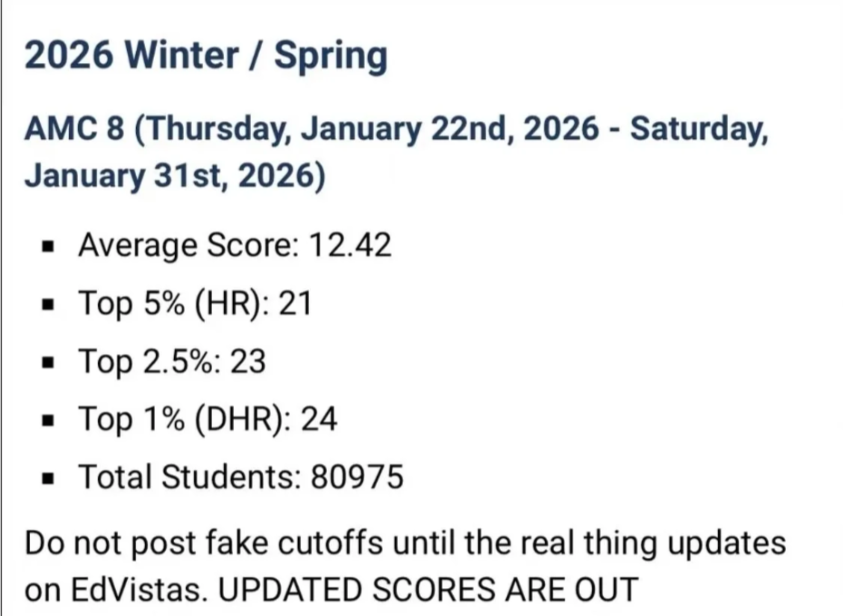
01AMC8
定位:
面向8 年级及以下学生,侧重数学兴趣启蒙与基础能力培养。
考试设计:
40 分钟完成 25 道选择题,满分 25 分。答对 1 题得 1 分,题目涵盖四则运算、几何图形、统计概率等 40 余个知识点。
02AMC10
定位:
面向10 年级及以下学生,衔接初中高阶与高中数学,是数学竞争力提升的关键跳板。
考试设计:
75 分钟完成 25 题,满分 150 分。答对 6 分 / 题,不答 1.5 分,后 5 题难度接近中国高中联赛二试水平,新增二次函数、立体几何等模块。
03AMC12
定位:
面向12 年级及以下学生,考察内容覆盖整个高中数学课程,是高阶数学思维的试金石。
考试设计:
75 分钟完成 25 题,满分 150 分,答对 6 分 / 题,不答 1.5 分。在 AMC10 基础上新增数论进阶、三角与复数、组合创新等。
AMC8/10/12如何规划?
AMC8
适合学生:建议3-8年级学生
核心目标:熟练掌握小学至初一数学知识,正确率≥80%
熟练掌握知识点:
🔆算数与代数:整数运算、分数 / 小数应用、一元一次方程、简单不等式、比例与百分数
🔆几何:平面图形面积 / 周长、简单立体图形体积
🔆组合与计数:枚举法、简单排列组合、容斥原理、概率基础
🔆数论初步:因数与倍数、质数合数、最大公约数 / 最小公倍数
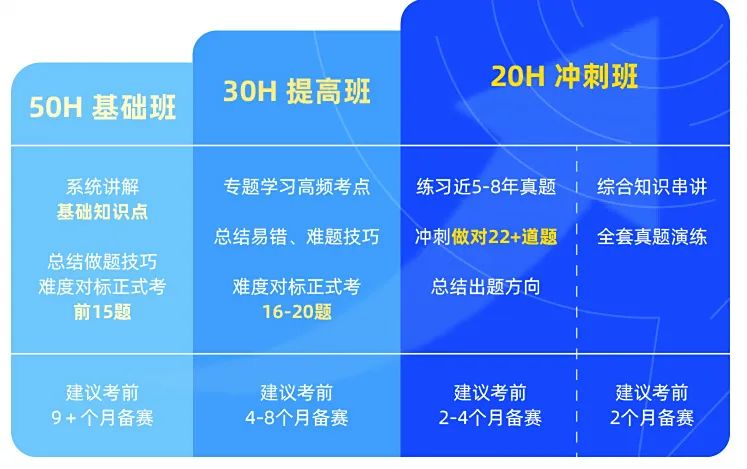
学习策略:
⌛备赛时间:建议6-9个月准备
💡基础期:用生活案例理解抽象概念,培养数学兴趣,奠定数学基础。
💡强化期:刷AMC8竞赛真题,总结高频题型的解题模板。每周限时40分钟训练 1 套真题,重点分析错题原因。
💡冲刺期:训练近5年的AMC8竞赛真题,尤其针对21-25题进行专项突破。
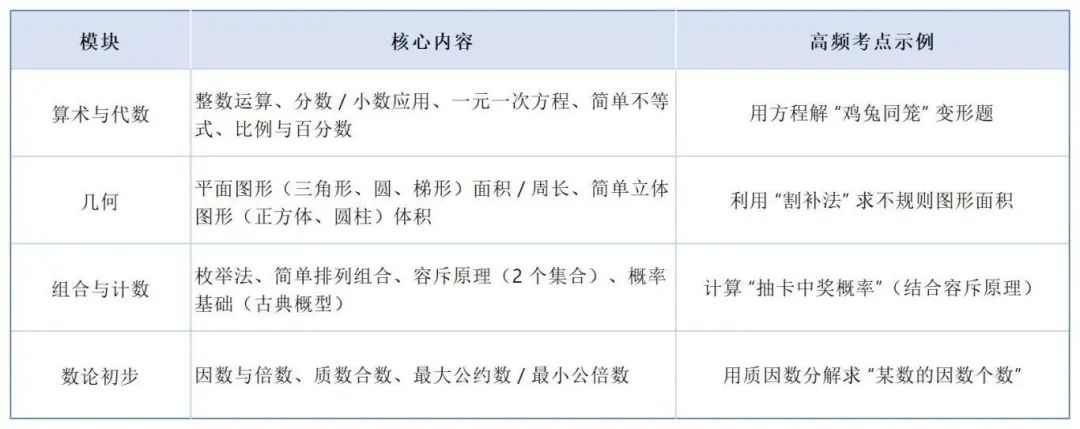
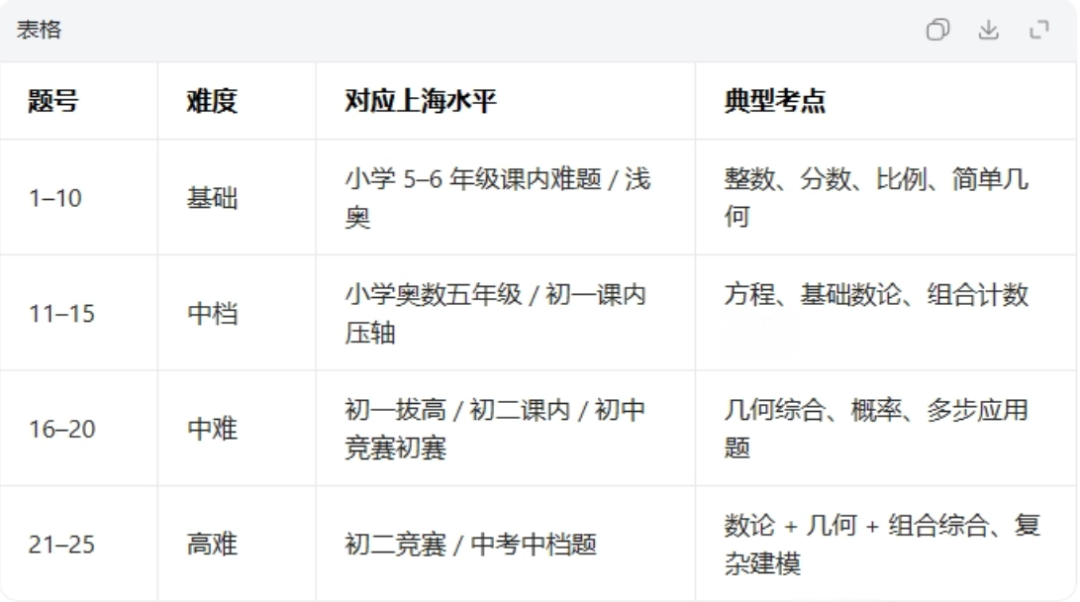
*AMC8核心知识模块
AMC10
适合学生:建议7-10年级学生
核心目标:掌握高中数学核心模块,正确率≥70%,后 5 题正确率≥40%
熟练掌握知识点:
🔆代数进阶:二次函数图像与性质、一元二次方程韦达定理、不等式、数列
🔆几何进阶:三角形五心、圆的性质、立体几何体积表面积
🔆数论深化:模运算、欧拉定理、不定方程、因数个数定理进阶
🔆组合进阶:排列组合进阶、概率进阶、递归计数、容斥原理
学习策略:
⌛备赛时间:建议提前1年准备
💡基础期:系统学习高中数学核心内容,每周分配 2-3 个模块,每个模块配套 20 道基础题进行训练。
💡强化期:按模块分类刷AMC10竞赛真题,训练 不答题策略,对完全没思路的题可战略性放弃,保证已答题目正确率。
💡冲刺期:刷近5年的AMC10竞赛真题,每周 2 次全真模考,模拟考场压力下的时间分配。
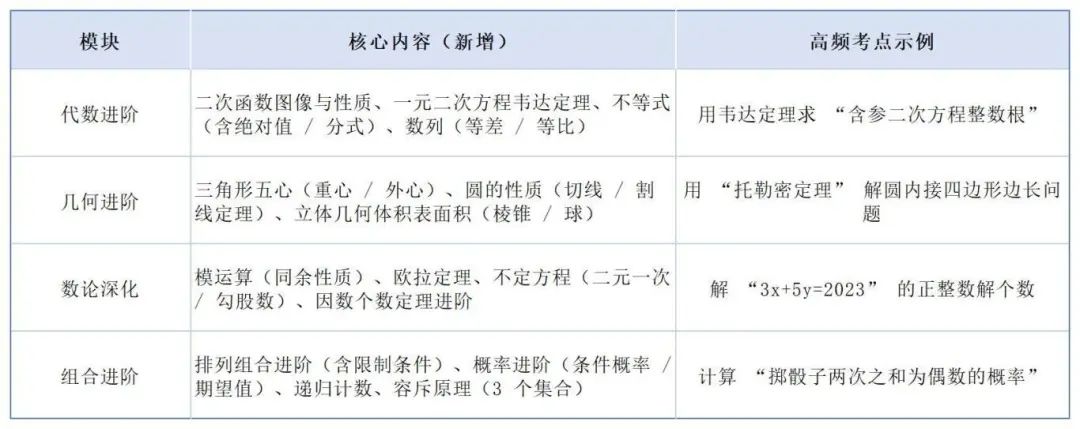
*AMC10核心知识模块
AMC12
适合学生:建议9-12年级学生
核心目标:掌握高阶数学模块,正确率≥60%,后 5 题正确率≥50%
熟练掌握知识点:
🔆代数高阶:复数的几何意义、多项式进阶、三角函数恒等式
🔆几何高阶:圆锥曲线、几何变换、球面几何初步
🔆数论高阶:二次剩余、同余方程、数论函数、不定方程
🔆组合高阶:生成函数、图论初步(路径计数)、概率分布、容斥原理
学习策略:
⌛备赛时间:在AMC10的基础上,建议提前1年准备
💡基础期:学习AMC12的知识点,进行高阶知识的攻坚。
💡强化期:按照难点专题深度学习,总结难题错题,进行学术思维训练。
💡冲刺期:刷近5年的AMC12竞赛真题和AIME前面5题。重点训练时间分配弹性,若前 15 题耗时超 40 分钟,需压缩后 10 题时间,优先保证中等难度题正确率。
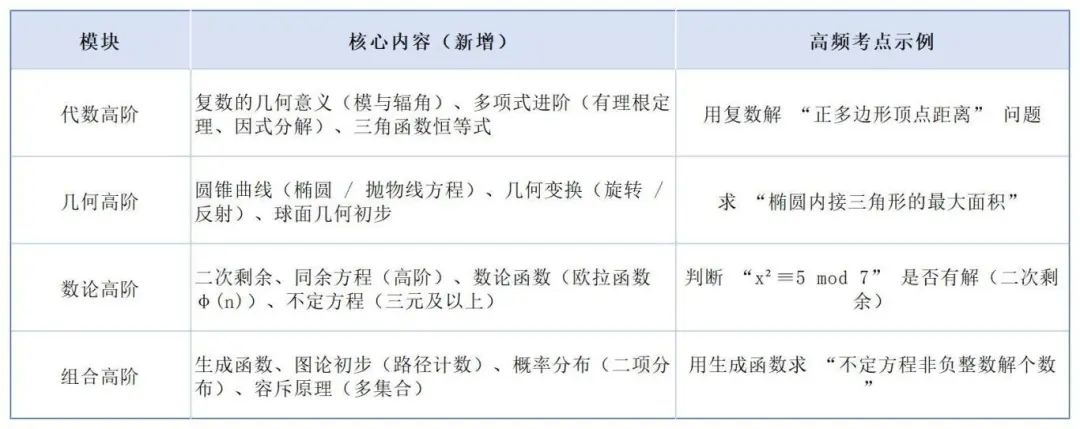
*AMC12核心知识模块
机构AMC竞赛辅导
在AMC 的高学术门槛下,从复杂题型的快速破题,到思维盲区的精准突破,每一步都考验着知识储备与思维深度,不少同学常因找不到适配的进阶路径而陷入瓶颈。
机构推出了AMC8/10/12培训课程,为不同阶段的你量身打造 “成长阶梯”,用系统化专业体系打破进阶壁垒。
课程设置
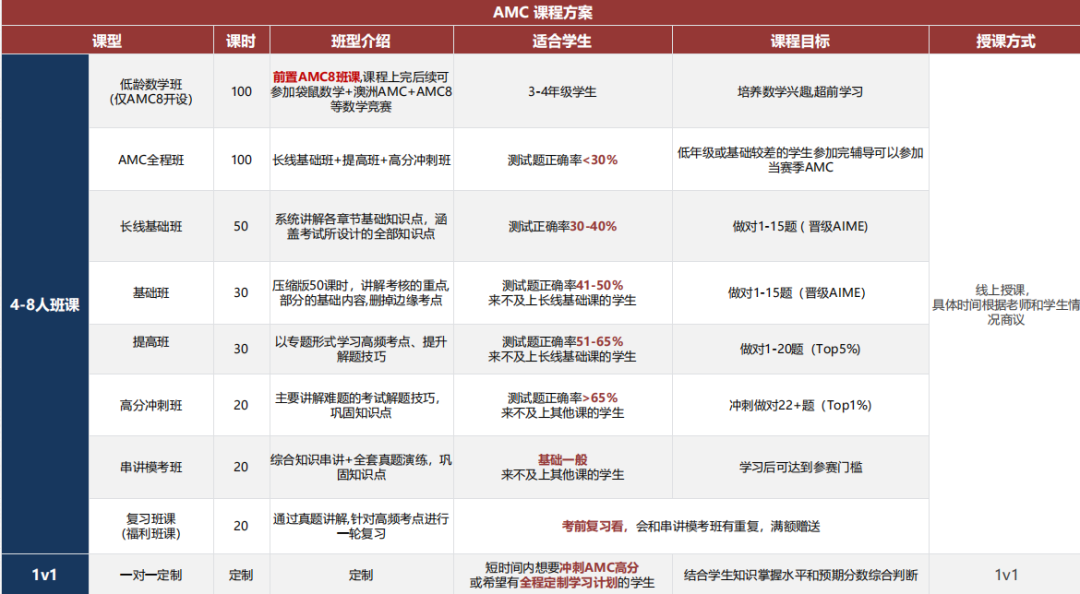
✅课程类型:4-8人小班/一对一授课
✅授课模式:线上/线下(深圳)同步开课
✅授课语言:中英双语教学/纯英文授课