AMC10是由美国数学协会(MAA)主办、面向10年级及以下学生的国际数学竞赛,在全球范围内含金量极高。对于中国学生而言,参与AMC10不仅是一次数学能力的检验,更是通往世界名校的重要"敲门砖"。
AMC10参赛优势
✅国内学校申请必备
顶尖高中认可:包玉刚、深国交、人大附中等全国知名高中,在自主招生中高度认可AMC10成绩。AMC10全球前5%(Honor Roll)已成为优质高中筛选学生的重要参考指标
综合评价加分:有很多学校将AMC10的成绩列为申请条件,而在强基计划、综合评价招生中也可以作为学术特长证明。
数学分班优势:部分国际学校、重点中学根据AMC10成绩进行数学分班,优秀学生可进入更高层次的班级学习。
✅国际学校招考利器
美本申请"硬通货":AMC10是申请美国顶尖大学(如MIT、斯坦福、普林斯顿等)的重要学术背景证明。AMC10全球前1%(Distinguished Honor Roll)或AIME晋级,在申请材料中具有显著竞争力
✅普娃可以考AMC10吗
AMC10的备考过程,本质上是高阶数学思维的系统训练。与校内数学不同。学习AMC10的过程中可以得到:
- 逻辑推理能力:通过复杂问题的分析,提升逻辑思维严密性
- 创新解题能力:鼓励一题多解,培养创新思维和灵活解题能力
- 时间管理能力:75分钟完成25道题,要求快速决策和高效解题
- 抗压能力:在竞赛压力下保持冷静,提升心理素质
这些能力不仅对数学学习有益,更对物理、计算机等学科学习有很大的帮助。
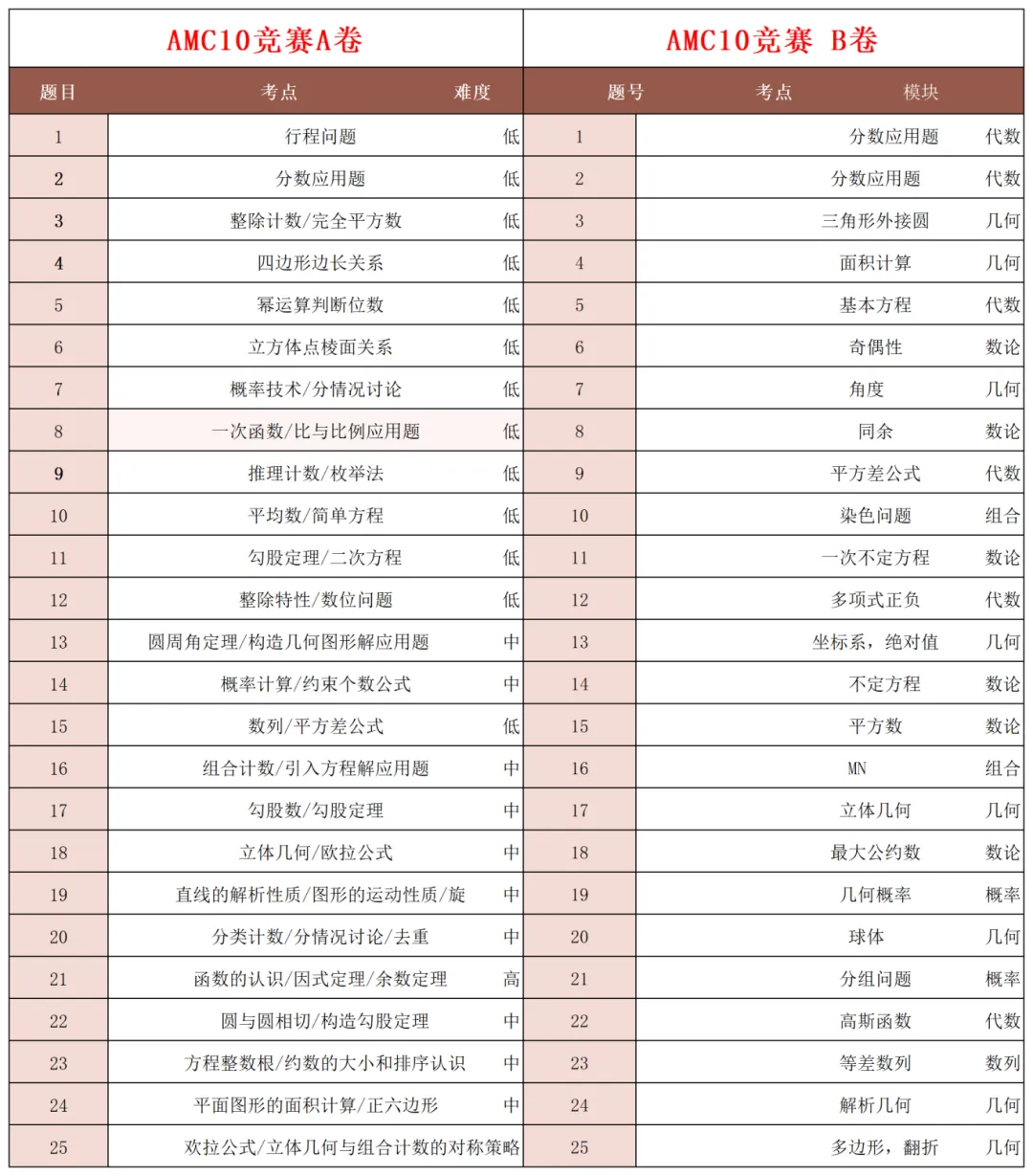
AMC10考察重点
AMC10的考试内容包含代数、几何、数论、组合四大核心模块,各模块占比和考察重点如下:
⭐️代数模块(约35%)
核心知识点:
- 一次、二次方程与不等式
- 函数与图像(一次函数、二次函数、绝对值函数)
- 数列与级数(等差数列、等比数列)
- 多项式运算与因式分解
- 指数与对数运算
考察特点:
- 注重代数变形技巧和运算能力
- 强调函数思想的应用
- 常与实际问题结合,考察建模能力
- 典型题型:方程应用题、函数最值问题、数列求和等
⭐️几何模块(约30%)
核心知识点:
- 平面几何:三角形、四边形、圆的基本性质
- 相似与全等
- 勾股定理及其应用
- 面积与体积计算
- 解析几何初步(坐标系、距离公式)
考察特点:
- 强调几何直观和空间想象能力
- 注重辅助线构造和几何变换
- 常与代数方法结合(数形结合)
- 典型题型:几何证明、长度/面积计算、最值问题等
⭐️数论模块(约15%)
核心知识点:
- 整除性质与同余
- 质数与合数
- 最大公约数与最小公倍数
- 不定方程
- 数位问题
考察特点:
- 概念抽象,逻辑性强
- 需要严密的推理能力
- 常与代数、组合结合
- 典型题型:整除问题、同余方程、质数性质应用等
⭐️组合模块(约20%)
核心知识点:
- 计数原理(加法原理、乘法原理)
- 排列与组合
- 概率初步
- 图论初步
- 组合恒等式
考察特点:
- 思维灵活,方法多样
- 强调分类讨论和构造能力
- 易出现"陷阱题"
- 典型题型:计数问题、概率计算、组合最值等
AMC10备考策略
由于AMC10数学竞赛的考察内容包含了初中和高一年级的数学知识点,对于初中参赛的学生来说还需要补齐知识点,建议备考时间6-8个月。
🔅基础阶段(2026年2月-6月)
知识梳理:系统学习代数、几何、数论、组合四大模块的基础知识,可参考权威教材(如《Art of Problem Solving》系列)或专业辅导资料,确保对每个知识点理解透彻。
建立错题本:整理练习和测试中的错题,分析错误原因(知识点漏洞、解题思路错误、粗心等),定期复习巩固。
🔅强化阶段(7月-8月)
专项刷题:针对不同模块进行分类刷题,重点突破薄弱环节。例如,几何模块可集中练习平面几何的辅助线构造、立体几何的空间想象问题;数论模块强化同余、整除等概念的应用。
总结解题模型:通过刷题总结常见题型的解题方法和技巧,如代数中的因式分解技巧、组合中的分类讨论方法等,提高解题效率。
🔅冲刺阶段(9月-11月)
真题模拟:每周进行1-2次全真模拟考试,严格按照考试时间(75分钟)和题型要求完成真题,适应考试节奏和时间压力。
时间分配优化:根据题目难度合理分配时间,建议前10题控制在15-20分钟内完成,中间10题每题2-3分钟,后5题根据难度适当调整时间,确保会做的题目尽量得分。
查漏补缺:通过模拟考试和错题分析,找出知识体系中的薄弱环节,进行有针对性的强化复习,巩固知识点和解题技巧。
AMC10备考教材
大家都知道备考AMC10要刷真题,其实要补齐AMC10的基础知识点同学们就需要用教材来学习。Tina老师给大家整理了这套AMC10的备考教材,希望能够帮助到大家。
AMC10这本教材聚焦教材中的例题与课后习题,不追求速度,每章节先吃透核心概念再动手刷题。重点标记“竞赛延伸知识点”

这本教材重点攻克二次函数、多项式、数列、不等式等高频考点,教材中的“挑战性习题”可选择性练习.每学完一个章节,整理“题型-解法”清单形成自己的解题框架。

这6套练习册是按教材分模块(代数、几何、数论、组合)进行专项训练,重点关注“考纲高频考点”。教材中的真题改编题优先做,做完后对照解析,标注自己的知识盲区,针对性补学。