5月20日的爱德思S1大考近在眼前,是不是感觉时间有点紧迫?别担心,俗话说得好:“临阵磨枪,不快也光!” 在这冲刺的最后阶段,为了助大家一臂之力,我们特别推出了2024年爱德思S1真题的逐题深度解析。

Q1

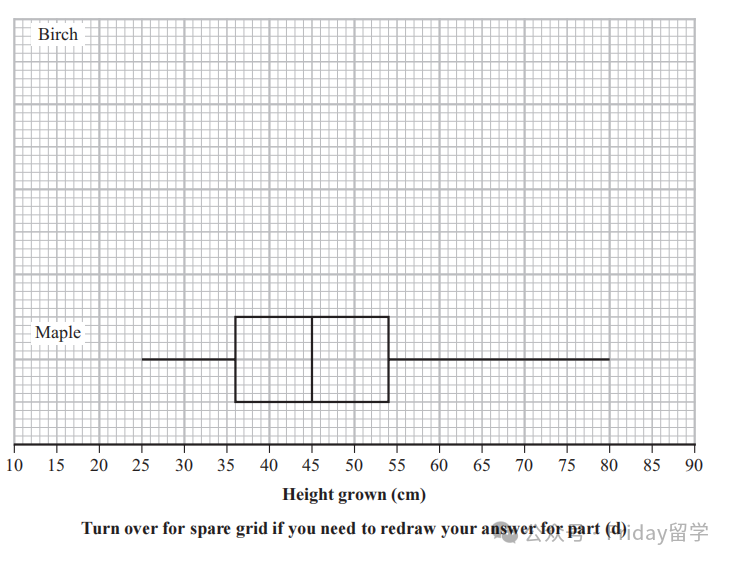
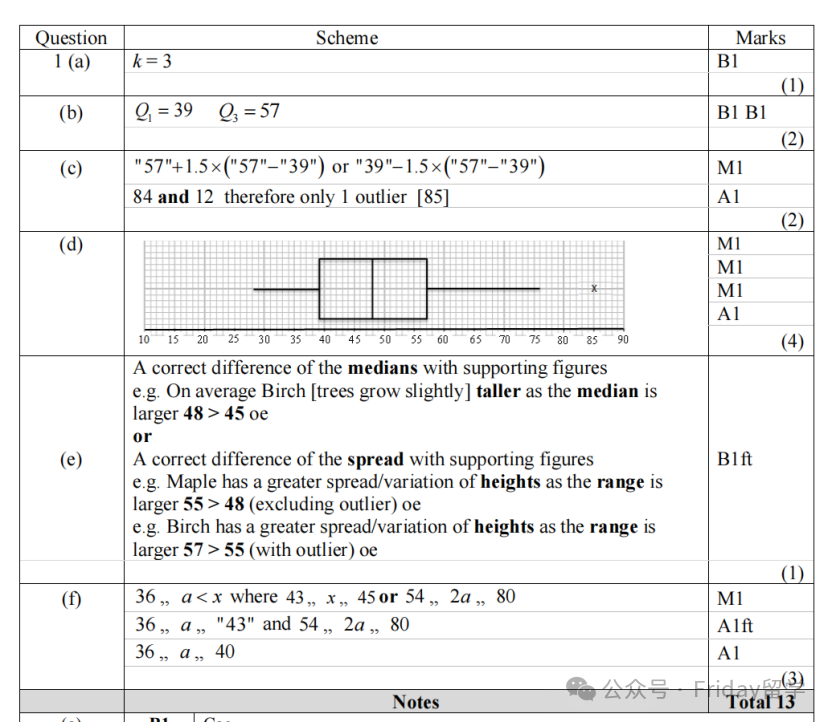
老师点评:第一题整体看还是中规中矩,通过茎叶图给数据,里面带个参数k 需要利用中位数信息反推。之后算Q1、Q3和Outlier(异常值)都是常规操作,Outlier公式也是书上给的1.5倍IQR,这部分是基本功,要稳拿。
这题的第一个得分关键和难点在于(e) 问的比较分布 (Comparing Distributions)。大家要注意,比较时要从集中趋势(Central Tendency) 和离散程度(Spread/Dispersion)两方面入手。从答案看,常见的比较角度是Median (中位数) 和IQR (四分位距),务必结合具体数值来支撑你的比较结论。
最具挑战性的无疑是最后(f) 问。它引入了新参数a,并告知加入新数据后枫树的箱线图不变。这个“不变”是解题的钥匙!这意味着原有的Q1、中位数、Q3都得保持原样。
因此,新加入的数据点(包含a和2a)就必须满足一定的条件,不能越过这些“雷池”。这主要考察大家能否从统计量的基本定义出发,为参数 a 找到它必须遵守的约束条件(constraints),非常考验逻辑判断能力。
Q2

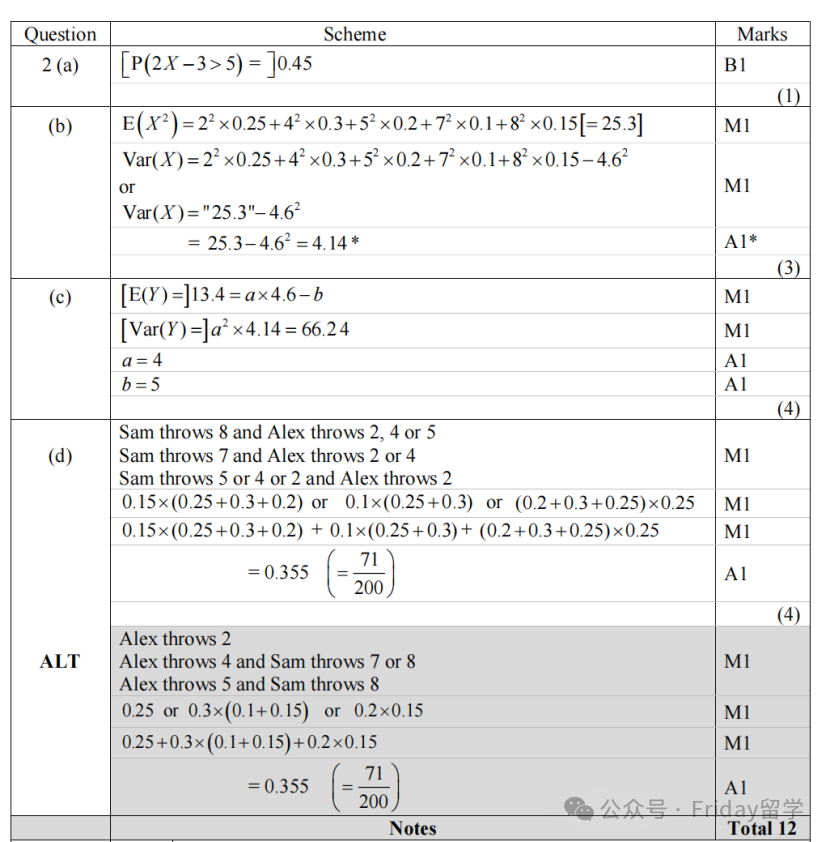
老师点评:第二题主要考察的是离散随机变量(Discrete Random Variable) 的相关知识。基础计算(a, b, c小问):这道题在前几问,比如计算概率P(2X - 3 > 5),以及期望 (Expectation) 和方差 (Variance) 的计算,可以说是中规中矩,基本都是直接套公式就能解决。Var(X) = E(X²) - [E(X)]²(用于b问证明)对于随机变量的线性变换Y = aX - b,其期望和方差的公式:E(Y) = aE(X) - bVar(Y) = a²Var(X)(用于c问求解a和b)。
大家在套用这些公式时,务必区分清楚谁是系数a,谁是常数 b,不要搞混。游戏概率与策略(d小问):这道题真正有意思且容易拉开分差的点,可能在于最后一部分关于Sam和Alex玩游戏的问题。他们每个人转一次转盘,但得分的计算方式(S = X₁ 和 R = 2X₂ - 3) 是不一样的。
要计算Sam获胜 (S > R) 的概率,最直接有效的方法就是把所有可能的 (X₁, X₂) 结果组合都列出来,然后逐一计算 S 和 R,判断Sam是否获胜,并累加对应组合的概率。很多同学一看到可能的情况比较多,就容易自己把自己吓倒,望而却步,甚至没尝试就放弃了。
其实,当你开始动手列举,哪怕只列出一部分,往往就能发现一些规律或者简化计算的模式。所以,遇到这类问题,一定要敢于尝试,动手去列,不要怕麻烦。细心和耐心是关键。
Q3

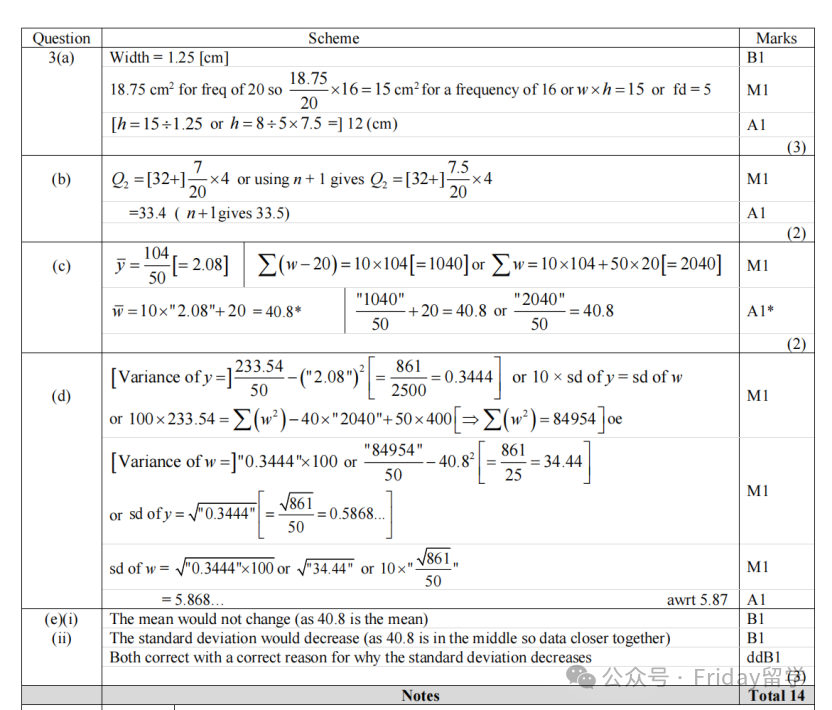
老师点评:这第三题是每年S1的必考内容——直方图(Histogram),这次放在第三问,考察点也算中规中矩。直方图核心性质(a小问):大家务必牢记:直方图中,小长方形的面积(Area) 与频数 (Frequency) 成正比,而不是高度!数据越多,面积越大。高度代表的是频率密度 (Frequency Density) (频率 / 组宽)。
第一问计算条形宽度和高度,可以用面积正比,也可以用高度正比于频率密度来求解。中位数估计(b小问):考察的是线性插值法(Linear Interpolation) 估计中位数。比如总共50个数据,中位数就是第25个。先找到第25个数据所在的组,然后利用该组的下限、组内频率、之前累积频率和组宽进行插值计算。这是个常用技巧,必须掌握。
数据编码(c, d小问):编码(Coding) 部分,我个人认为相对容易。无非是理解编码公式 (w = 10y + 20),然后进行正向或反向推算。关键是记住编码对平均数 (w̄ = 10ȳ + 20) 和标准差 (sd(w) = 10 * sd(y)) 的影响规则。新数据的影响分析(e小问):最后讨论新加入一个数据点(恰好是原平均数40.8g)对统计结论的影响。
对平均数:加入一个等于原平均数的值,新的平均数不变。对标准差:数据因为新加入了一个“中心点”而变得更集中了,所以标准差会减小。这一点可能对部分同学来说有点绕,需要想明白。
直方图的定义(面积与频数成正比)和线性插值法是重中之重。e小问这种解释性问题,如果考试时实在没思路,有时战略性放弃(通常1-2分)也是可以接受的。
Q4

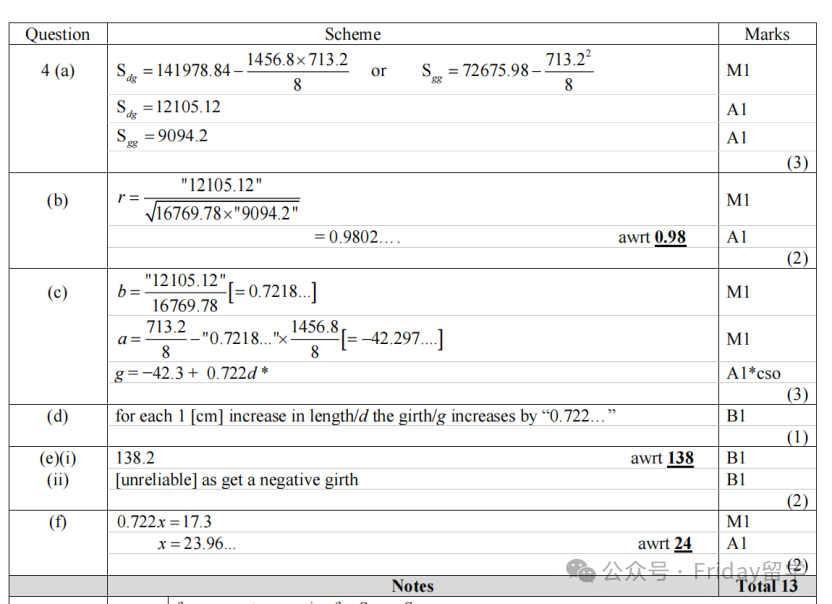
老师点评:这第四题是关于相关与回归(Correlation and Regression) 的,整体来看还是比较中规中矩。
只要大家能看懂题目背景(关于熊的长度和胸围数据),理解变量的含义,问题就不大。核心公式与计算(a, b, c小问):计算S_dg, S_gg (以及 S_dd,题目已给) 是基础,它们对应公式表里的 S_xy, S_yy, S_xx。积差相关系数(PMCC) r 的计算公式 r = S_dg / √(S_dd * S_gg) 也要熟练运用。重要提示:注意r 的分子 S_dg 是一次项(单位相乘),分母根号下 S_dd * S_gg 是2次项,开方后是1次项(单位的平方)。
所以r的分子分母量纲是一致的,因此 r 是一个没有单位的纯数,其值介于 -1 和 1 之间。 越接近±1,线性相关性越强;越接近0,线性相关性越弱。回归直线方程g = a + bd 的求解, b = S_dg / S_dd,a = ḡ - b * d̄。这些公式需要准确套用并写出计算过程。计算器的妙用:虽然考试需要写出公式和步骤,但强烈建议大家学会使用计算器直接求解回归方程的功能(不同型号计算器操作略有不同,请提前熟悉)。这对于验算结果非常有帮助,能有效避免计算失误。
回归方程的解释与限制(d, e, f小问):解释斜率b 的实际意义是常考点。更重要的是回归方程的适用范围/限制(e小问的(ii))。当用回归方程进行预测时,如果给定的自变量值超出了原始数据的范围 (Extrapolation),那么这个预测结果就是不可靠的。这是因为我们不能假设线性关系在数据范围之外依然成立。
Q5

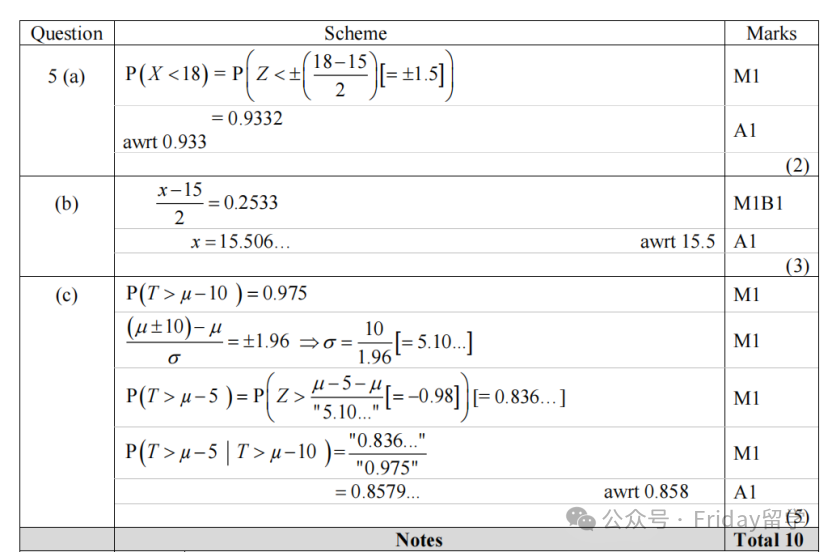
老师点评:这第五题是关于正态分布(Normal Distribution) 的,整体来看,题目设计得相当中规中矩。
正向与逆向计算(a, b小问):主要考察了正态分布的两种基本运算:正向计算:已知随机变量X 的边界值,去求它发生的概率 (如 P(X < 18))。
逆向计算:已知某个事件发生的概率,反过来去求随机变量X 的边界值 (如找到 x 使得 P(X < x) = 0.60)。
对于这两种计算,我还是希望大家查表法和计算器法都要熟练掌握。计算器可以作为非常好的验算工具,确保结果的准确性。
当然,最核心的是要牢记原始正态分布X 与标准正态分布 Z 之间的变换公式:Z = (X - μ) / σ。正态分布与条件概率的结合(c小问):这道题的后半部分,是一个非常典型的将正态分布与条件概率(Conditional Probability) 相结合的考察点。
首先,大家必须牢记条件概率的基本公式:P(A|B) = P(A∩ B) / P(B)。当正态分布与条件概率结合时,一个经常出现的情况,也是由正态分布自身连续且单峰的特性决定的,就是在计算分子P(A ∩ B) 时,事件A和事件B往往存在包含关系。
比如,题目中的 P(T > μ - 5 | T > μ - 10),事件 A: T > μ - 5 本身就蕴含了事件 B: T > μ - 10 (即A是B的子集),所以它们的交集 A ∩ B 就等于事件 A。识别出这种关系能极大简化计算。这部分是本题的难点,需要大家特别注意。
Q6
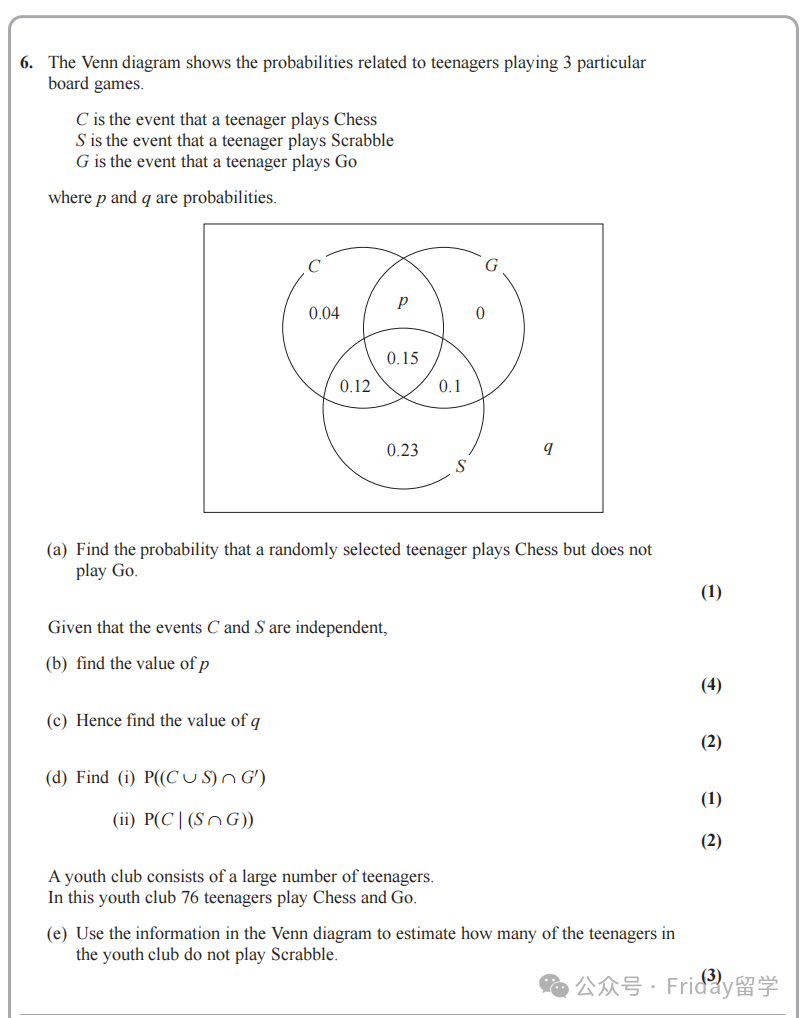
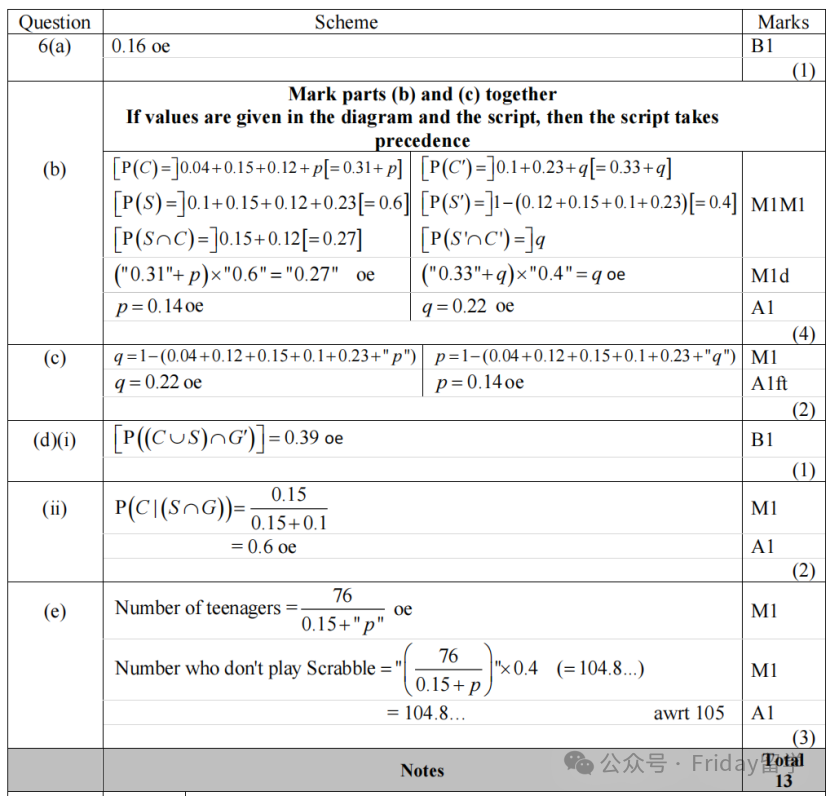
老师点评:第六题先考察的还是大家的读题能力。有同学考试时可能不认识‘Scrabble’(拼字游戏)这个词,但这不影响解题,只要能看出是三种游戏即可。
所以,统计题中遇到生词,大家完全可以结合上下文猜测词义。另外,很多同学拿到韦恩图就想立刻把所有未知数(如图中的p 和 q)解出来。
但大家会发现,初始信息往往不足,需要结合题目后续给出的条件(比如事件的独立性)才能逐步求解。这道题对韦恩图(Venn Diagram) 的理解和运用考察得比较重,大家需要熟练掌握集合的交、并、补在图中的表示和它们之间的联系。这方面内容在本题中考得比较多。
虽然前面的题目也考了条件概率,但这道题的(b) 小问重点考察了事件的独立性 (Independence)。这里要特别强调一个非常重要的概念区分:两个事件如果是互斥(Mutually Exclusive) 的,在韦恩图上是可以很直观地看出来的(表现为两个圈没有重叠部分)。
但如果两个事件是独立(Independent) 的,在韦恩图这种概率图上是看不出来的!独立性必须通过定义式 P(A∩B) = P(A)P(B) 来进行判断或应用。如果画成树状图 (Tree Diagram),独立性会表现得更直观一些。
最后,(d)小问再次考察了条件概率,这也是S1中非常经典和高频的考点,属于常规操作。对于韦恩图问题:不要被生词吓倒,理解大意即可。不要期望一开始就能解出所有未知数,善用题目后续给出的条件。
牢固掌握交集、并集、补集的概念及其在图中的表示。清晰区分“互斥”和“独立”:互斥看图,独立算数。
条件概率公式P(A|B) = P(A∩B) / P(B) 必须熟练。
以上就是我们对2024年爱德思S1夏季大考这份真题的逐题解析和点评。
整体来看,这份S1卷子延续了爱德思一贯的风格,题目设置“中规中矩”之中不乏对细节和综合运用能力的考察。
从第一题的数据图表解读,到离散随机变量的计算,再到直方图与编码,接着是相关与回归的深入分析,然后是正态分布与条件概率的结合,最后以经典的韦恩图概率问题收尾——可以说,S1的核心考点基本都得到了覆盖。
同学们在复习时,我们建议:夯实基础,公式要烂熟于心:无论是期望方差、相关系数、回归方程,还是正态分布的标准化,这些都是S1的“硬通货”。
注重理解,切忌死记硬背:比如直方图面积代表频数、回归系数的实际意义、独立与互斥的区别、条件概率的逻辑,这些都需要真正理解才能灵活运用。
细心审题,抓住关键信息:单位换算、题目中的特定条件(如独立性、特定数值)、图表中的隐含信息等,都是解题的关键。
善用工具,计算器是你的好帮手:尤其是在回归分析、统计量计算等部分,熟练使用计算器可以大大提高解题效率和准确率,但切记过程分同样重要。
最后的冲刺阶段,希望大家能够回归教材和笔记,查漏补缺,针对自己的薄弱环节进行强化训练。保持良好的心态,考试时沉着冷静,仔细分配时间,相信大家都能发挥出自己的最佳水平!














