新加坡国立大学博士导师（包焕臣教授）介绍

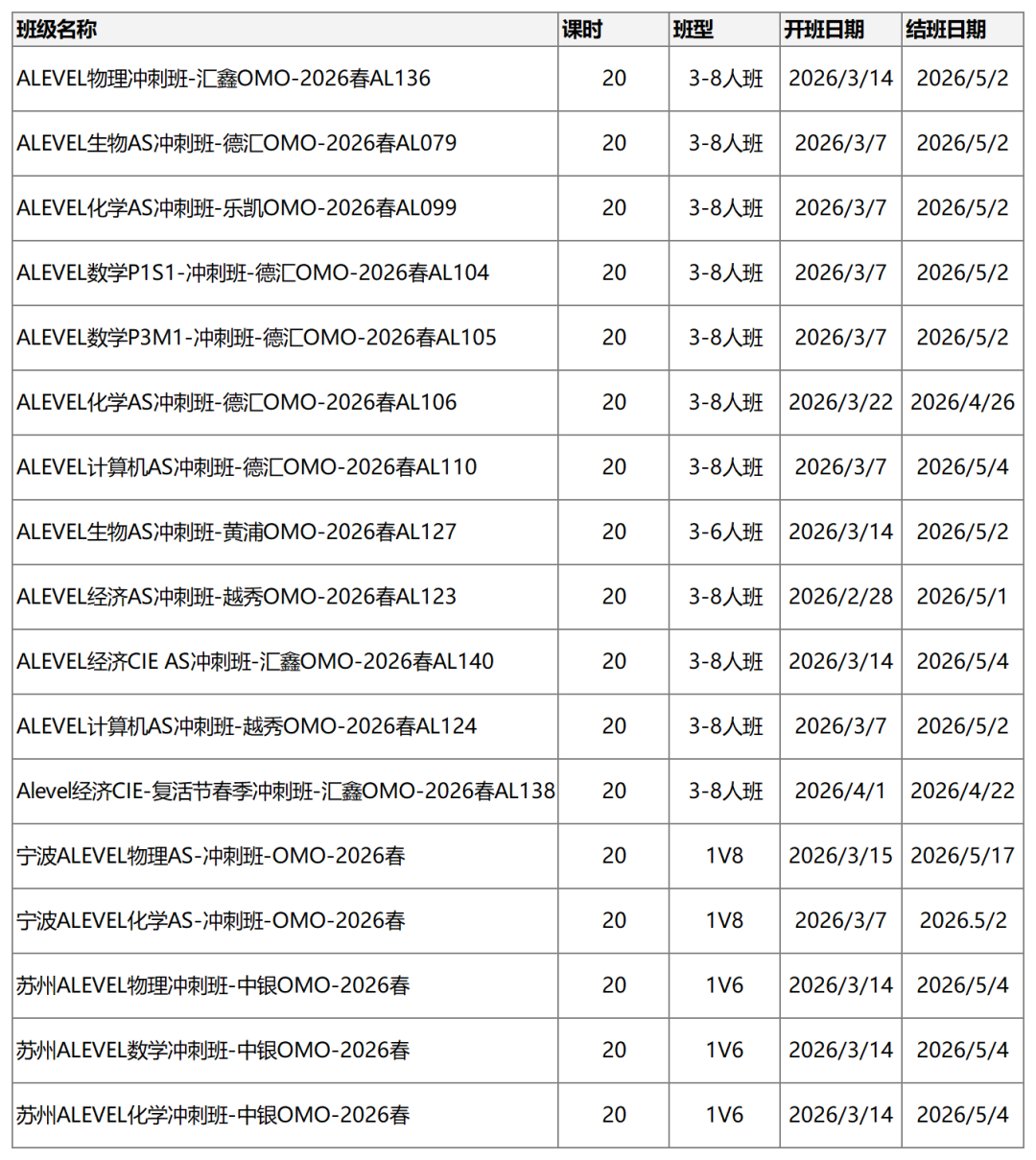
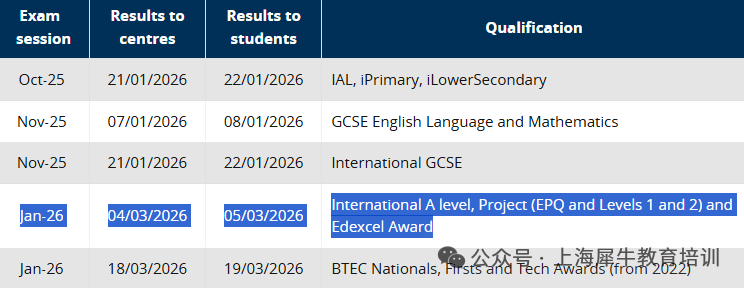
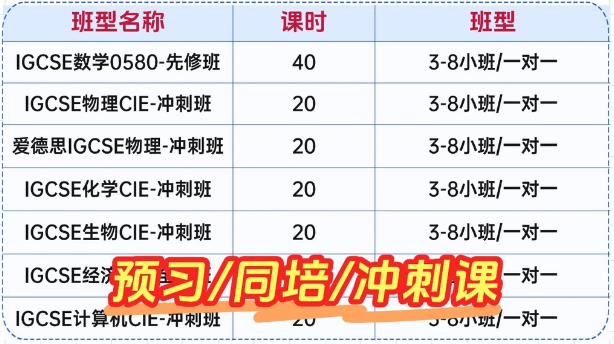
招生要求

新加坡国立大学（NUS）作为亚洲顶尖学府，其数学系PhD项目在学术界享有盛誉。包焕臣教授作为该校数学系杰出学者，现面向全球招收博士研究生，详细要求如下：

学术条件

· 学位背景：申请者须持有数学或相关领域的优秀本科学位（荣誉学位尤佳）

· 成绩标准：GPA须达3.0-3.5（满分4.0）或85%-90%以上

· 学术基础：应对表示论、代数学等相关领域有扎实理论基础

· 研究经验：具备相关研究经历将获优先考虑，但非必需条件

语言与测试

· 英语能力：非英语为母语且先前学位非全英文授课者需提供以下证明之一：

• IELTS：不低于6.5-7.0
• TOEFL iBT：不低于92-94分

· GRE考试：虽为可选项，但提交优秀成绩能显著提高录取几率

• 学术成绩特别突出者可申请豁免GRE要求

申请流程

· 材料清单：

• 完整在线申请表格
• 学术成绩单与学位证明
• 研究计划书（重点阐述对量子群、李代数等领域的研究兴趣）
• 个人陈述（研究动机、学术志向与职业规划）
• 至少两封学术或专业推荐信
• 详实个人简历
• 已发表论文或研究摘要（若有）

· 截止日期：

• 8月入学批次：前一年11月15日
• 1月入学批次：前一年5月15日
• 强烈建议参与第一轮申请，以获全额奖学金优先评估机会

奖学金详情

· 全额资助：NUS Research Scholarship覆盖全部学费并提供生活津贴

· 津贴标准：

• 国际学生基础月津贴：SGD 2,000-2,700
• 通过PhD资格考试后可额外获得最高SGD 500/月

· 资助期限：最长4年，每学期评估续期

· 无服务约束：毕业后无工作服务承诺要求

研究方向

包焕臣教授作为NUS数学系副教授，其研究涵盖代数表示论多个前沿领域。他曾在顶尖学术期刊如Inventiones Mathematicae、Advances in Mathematics和Compositio Mathematica等发表多篇高影响力论文。其主要研究领域包括：

量子群与对称对理论

· 量子对称对的基础理论：构建和分析量子对称对(quantum symmetric pairs)的代数结构

· 正则基研究：开创性地构造了量子对称对的i-正则基(i-canonical bases)

· Kac-Moody拓展：将量子对称对理论从有限型拓展到Kac-Moody型

· 一次单位根研究：探索量子对称对在一次单位根处的特殊性质

李代数与李超代数

· 表示理论创新：研究李代数、李超代数及其量子变形的表示

· Kazhdan-Lusztig理论：开发正交辛李超代数(osp)的新型Kazhdan-Lusztig理论

· 范畴化方法：通过范畴化角度理解李理论的深层结构

· 模块分类：对不同类型李结构的模表示进行系统分类

代数几何交叉研究

· 旗簇几何：研究旗簇(flag varieties)的代数与几何性质

· 全非负性理论：探索全非负旗簇的细胞分解和正则性定理

· Richardson簇：分析Richardson簇的上簇结构及其应用

· 半域构造：开发半域(semifields)上旗流形的新理论

范畴化与量子理论

· 代数结构范畴化：将抽象代数结构提升到范畴层面

· Hecke代数范畴化：构造参数为1和v的Hecke代数的范畴化

· 张量积结构：研究张量积的正则基与超Kazhdan-Lusztig理论

· 量子对称性应用：探索量子对称性在物理学中的应用

包教授的研究工作结合了深刻的理论洞察与丰富的应用前景，为有志于代数表示论领域的博士生提供了广阔的学术发展空间。

Mason博士有想法

基于包焕臣教授的研究方向，以下是四个具有创新性且可行的研究计划构想：

1. Kac-Moody型量子对称对的几何实现与范畴化

本研究计划旨在拓展包教授在量子对称对领域的开创性工作，特别是其在Compositio Mathematica发表的成果，将其理论推广到更广泛的几何与范畴背景下：

· 几何模型构建：通过旗簇和箭图簇(quiver varieties)为Kac-Moody型量子对称对建立具体几何模型

· 范畴化理论拓展：系统发展量子对称对的范畴化理论，拓展有限型情况下的已有成果

· 结构联系探索：研究这些范畴化结构与Soergel双模和KLR代数之间的内在联系

· 拓扑学应用：探索量子对称对范畴化在低维拓扑学中的应用潜力，尤其是结绳不变量构造

此研究将填补量子对称对理论与几何表示论之间的关键空白，为量子群理论带来全新视角。

2. 全非负旗簇的计算结构与应用

基于包教授在Inventiones Mathematicae发表的关于全非负旗簇的突破性研究，本项目将：

· 算法开发：设计高效算法计算Kac-Moody群全非负旗簇的参数化和精细结构

· 簇代数联系：深入探索全非负旗簇与簇代数(cluster algebras)和整合系统的内在联系

· 优化理论应用：研究全非负性在半正定矩阵优化和凸几何中的应用价值

· 量子信息拓展：建立全非负旗簇与量子信息理论中纠缠结构的可能联系

该研究不仅将为抽象数学理论提供具体计算工具，还将拓展其在优化和量子科学中的实际应用。

3. 量子对称对与超对称理论的深层联系

本研究探索量子对称对理论与物理学中超对称理论的深层联系，特别结合包教授对amplituhedron的研究：

· i-正则基物理解释：研究量子对称对i-正则基在超对称理论计算中的表现与意义

· 振幅计算新方法：建立量子对称对与超对称杨-Mills理论散射振幅的计算联系

· AdS/CFT应用：探索量子对称对在超弦理论和全息对应原理中的应用可能

· 计算工具创新：开发基于量子对称对的新型计算工具，简化超对称理论中的复杂计算

此跨学科研究方向有望在理论物理与数学的交叉领域开辟新的研究前沿，产生重要理论突破。

4. 量子对称对与人工智能的创新融合

本研究计划探索量子对称对理论在现代人工智能和数据科学中的创新应用：

· 不变特征提取：利用量子对称对的正则基构造新型的机器学习特征提取方法

· 对称性结构学习：开发基于李代数和量子群结构的深度学习架构，提高模型对称性理解能力

· 拓扑数据分析：研究如何将量子对称对的不变量应用于复杂网络和高维数据的拓扑分析

· 量子算法优化：探索量子对称对在量子机器学习算法设计中的潜在革新作用

这一前沿交叉研究不仅为人工智能带来全新的数学工具，也为抽象代数理论开辟实际应用的广阔天地。