AMC8 内容全解析｜Topic 1：周长与面积（Perimeter & Areas）

每到学年交替，家长和学生都会问：

“数学应该怎么复习？”

“孩子的基础够不够？哪些知识点还没掌握？”

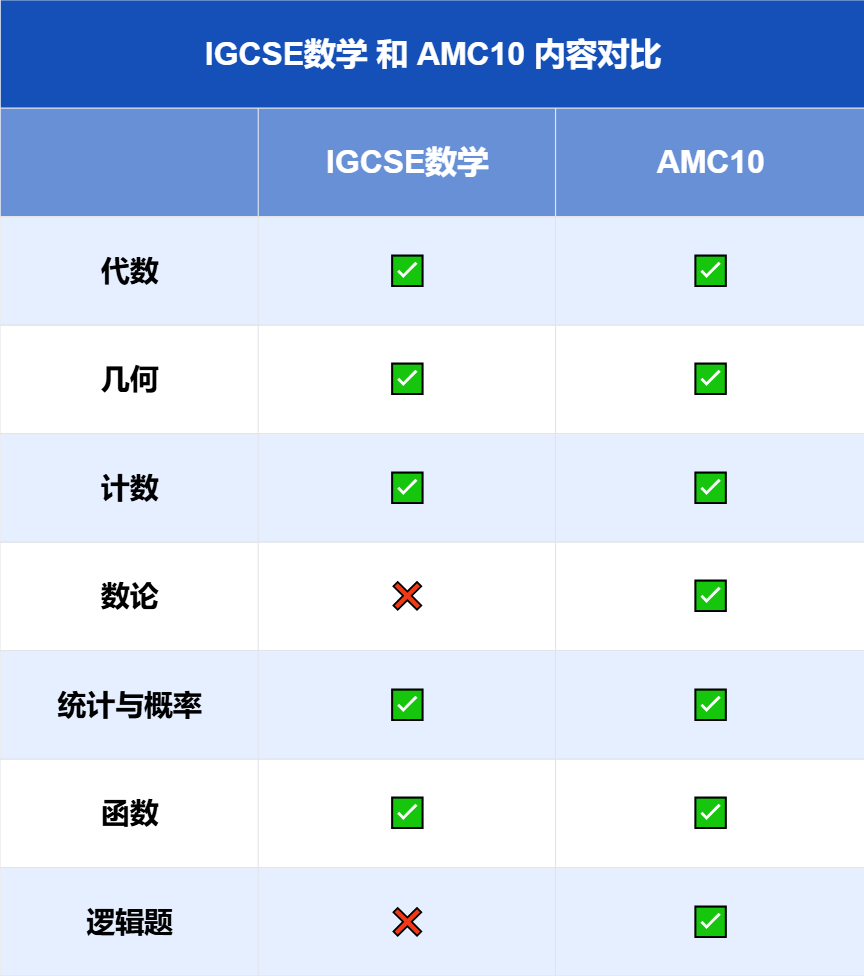
事实上，AMC8 是最好的复习与查漏补缺框架。

作为全球广受认可的中小学数学测评，AMC8 的 30 个核心知识点 几乎覆盖了小学到初中阶段必须扎实掌握的全部基础内容。

即便不以竞赛为目标，AMC8 也能帮助学生在假期里 系统梳理、查漏补缺、重建数学思维体系。

从本期开始，我们将把这 30 个知识点拆解为系列内容，让学生在假期中轻松实现逐点突破，迎接新学年的数学提升。

1、周长与面积

Perimeter and Areas

这是几何模块的重要基础，贯穿 AMC8 从 基础题 → 中档题 → 高难题 的全难度区间。

需要强调的是：AMC8 的几何题不是“背公式”就能得分。更关注学生是否具备：

1. 图形拆分能力

2. 条件转换能力

3. 逻辑推断能力

4. 几何与数论/代数结合的综合能力（高难题核心）

以下按照 2026 AMC8 新考纲 + MAA Topic List 进行系统讲解。

一、AMC8 Topic 1 知识点结构（2026 适用）

（1）基础层（第 1–15 题）

适合小学高年级至初一学生

•长方形、正方形周长

•三角形、平行四边形、梯形的基本面积

•简单复合图形的拆分

•网格图计算面积

•单位换算（cm²、英寸、m²）

（2）中等难度（第 16–20 题）

AMC8 命题的“常考策略题”

•复杂复合图形的拆分与拼合

•缺角型 / 镂空型面积

•固定周长 vs 面积变化型题

•折纸题、拼图题（AMC8 常考）

•坐标几何中的长度 / 面积

•几何逻辑推断（AMC8 特色）

（3）高难度（第 21–25 题）

AMC8 真正的拉分点

•周长/面积与数论结合（gcd、lcm、余数）

•网格点 + Pick’s Theorem 的隐性考察

•三角形面积 + 比例 + 分割推理

•平移/旋转后保持面积不变的推断

•周长固定求最大面积（经典优化类）

二、Past Paper 真题（按难度从易到难）

以下为每个难度段精选 2 题，共 6 题，帮助学生快速理解 AMC8 的题型结构。

A. 基础题（第 1–15 题）

题 1｜AMC 2017 Q5（基础面积）

长方形长 8、宽 6，面积是多少？

解析：8 × 6 = 48

答案：D

题 2｜AMC 2019 Q7（周长基础）

正方形周长 24，面积是多少？

解析：边长 6 → 6² = 36

答案：C

B. 中等题（第 16–20 题）

题 3｜AMC 2015 Q17（复合图形面积）

6×6 正方形挖去 3×3 小正方形，剩余面积？

解析：36 − 9 = 27

答案：B

题 4｜AMC 2018 Q19（网格图面积）

图形由 6 个完整小格 + 2 个半格构成。

解析：6 + 1 = 7

答案：7

C. 高难题（第 21–25 题）

题 5｜AMC 2016 Q22（周长 + 坐标几何）

三角形顶点为 (0,0), (6,0), (0,8)，求周长。

解析：6 + 8 + √(36+64) = 6 + 8 + 10 = 24

题 6｜AMC 2020 Q23（面积 + 数论）

10×10 正方形被分成若干小矩形，每块面积为 5 的倍数，最少分成多少块？

解析：100 ÷ 5 = 20

三、Topic 1 常错点总结

1.忽视隐形面积

如镂空、折纸题，面积被“隐藏”，需还原图形来源。

2.周长与面积变化混淆

AMC8 常用陷阱：

•面积变了，但周长不变

•周长变了，但面积不变

3.复合图形分割策略不熟练

AMC8 强调“分解 → 重组”，而非死记公式。

4.单位陷阱

常见混淆：平方英寸 vs 英寸；cm vs cm²。

5.坐标几何不熟悉

尤其是斜边公式 √(a² + b²) 的灵活应用。

结语

让数学学习真正扎实落地

数学的提升从来不是一蹴而就，而是不断积累与强化的过程。

AMC8 的 30 大知识点，为学生提供了最体系化、最清晰的学习地图。

通过逐点拆解、逐步突破，孩子不仅能掌握竞赛必考点，更能彻底建立数学思维能力。

接下来我们将继续连载 Topic 2–30，帮助学生在假期中轻松构建完整的数学框架，以最佳状态迎接新学年。

附AMC8 系统课程介绍

AMC8 的体系非常完整，因此 PGA 采用全年滚动开班，让孩子随时进入最适合的学习阶段。

无论孩子基础如何，都能找到适合自己的路径，从容应对 2026 AMC8。

01、36小时 · 全年体系班（基础 + 高阶全覆盖）

覆盖全部 30 个核心知识点，是从基础到冲刺的完整路线。

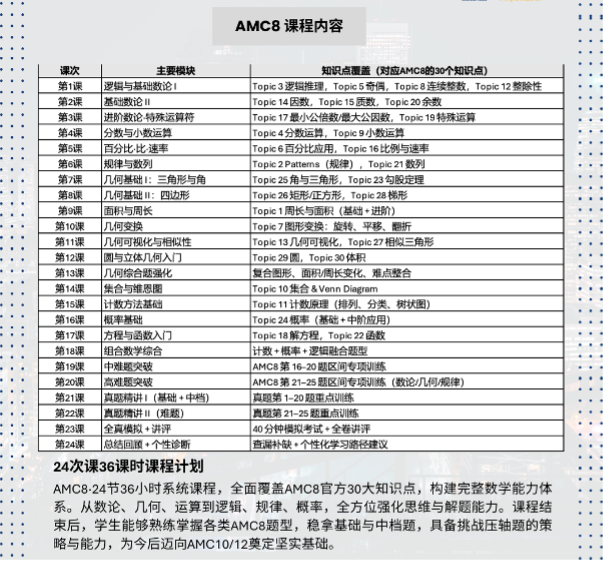
02、24小时 · 核心提升班（强化中档 + 高频考点）

适合基础良好、需要提高稳定得分能力的学生。

03、15小时 · 冲刺班（短期快速提分）

最新真题 + 解题技巧 + 模考评估，适合考前突破。