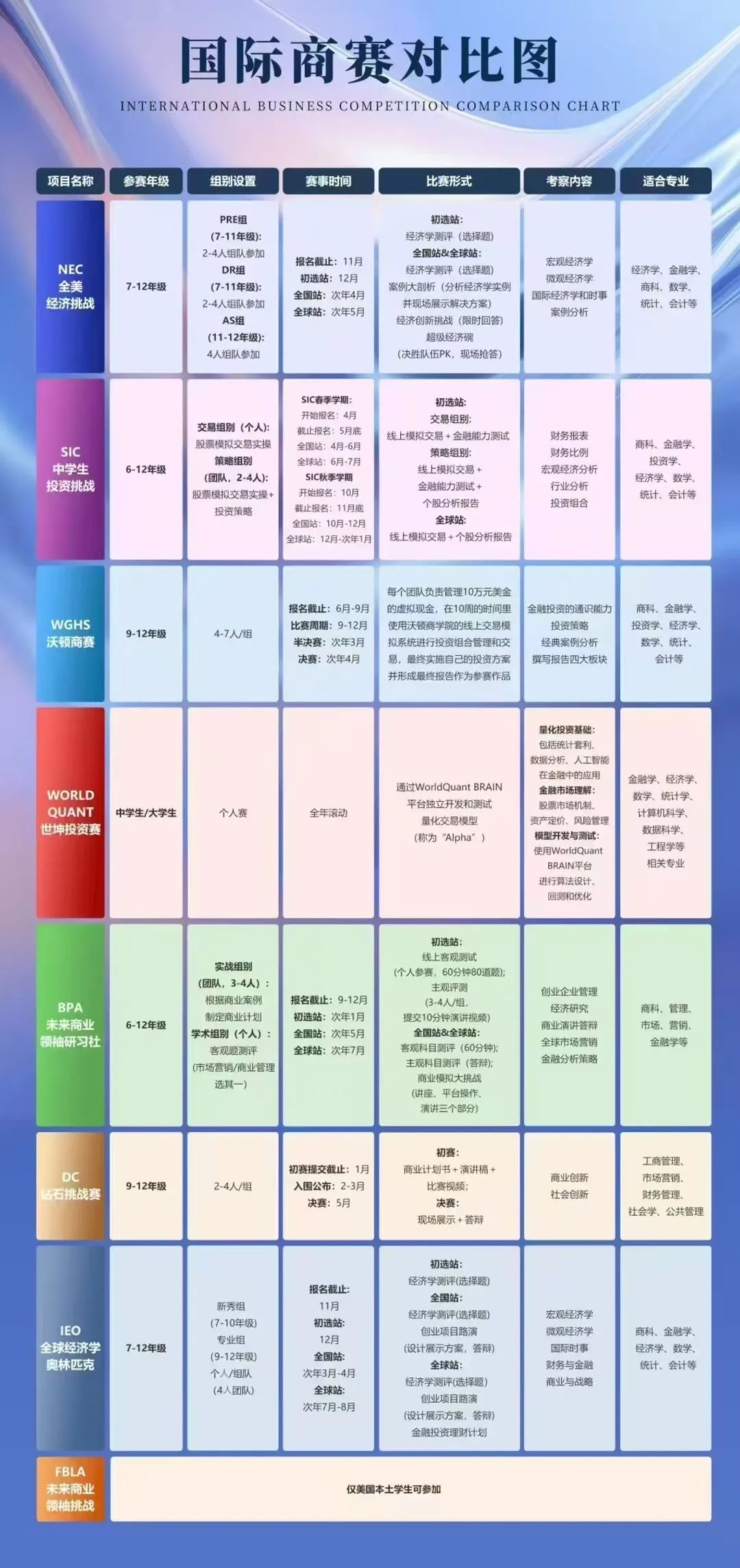
文章目录[隐藏]
微积分是一门重要的数学分支,涵盖了变化和运动的研究。本文将探讨微积分的基本概念、历史背景、主要应用以及学习方法等方面,旨在帮助读者更深入地理解这一领域。具体内容包括:1. 微积分的定义与基本概念;2. 微积分的发展历程;3. 微积分的基本定理;4. 微积分在实际生活中的应用;5. 学习微积分的方法与技巧;6. 常见问题解答。通过这些内容,读者能够全面了解微积分的重要性及其在不同领域中的应用。
一、微积分的定义与基本概念
微积分通常分为两大部分:微分和积分。微分主要关注函数变化率,而积分则涉及累积量。这两者之间有着密切的联系,形成了基础的“微分-积分”理论。
1. 微分
微分是研究函数如何随着自变量变化而变化的一种方法。它可以用来计算切线斜率,也就是某一点上函数值变化的速率。例如,如果有一个函数 f(x),其导数 f'(x) 表示 x 处的瞬时变化率,可以通过以下步骤计算:
- 选择一个点 x。
- 计算 f(x + h) 和 f(x) 的差值,其中 h 是一个非常小的增量。
- 将差值除以 h,然后取 h 趋近于零,这样就得到了导数 f'(x)。
2. 积分
与微分相对,积分则是将无穷小量进行累加,从而求出总量。简单来说,定积分可以理解为求曲线下方区域的面积。例如,对于函数 f(x) 在区间 [a, b] 上的定积分,可以通过以下步骤计算:
- 将区间 [a, b] 分成 n 个小区间,每个小区间宽度为 Δx。
- 在每个小区间内选择一个点 xi,并计算 f(xi) 的值。
- 累加所有小矩形面积,即 S = Σf(xi)Δx。
- 当 n 趋近于无穷大时,S 的极限即为定积分。
二、微积分的发展历程
微积分的发展经历了漫长而复杂的历史。从古希腊时期到17世纪,许多数学家为这门学科奠定了基础。
1. 古代起源
古希腊数学家如阿基米德曾利用几何方法来近似计算曲线下方区域面积。他们虽然没有正式定义极限,但他们的方法为后来的发展提供了启示。
2. 牛顿与莱布尼茨
17世纪末,牛顿和莱布尼茨独立发展出了现代意义上的微积分类。在这个过程中,他们引入了极限、导数和定积等关键概念,为后来的数学分析打下基础。
3. 数学严格化
19世纪初,随着实分析的发展,数学家们开始对微积分类进行了严格化处理,使之成为一门成熟且严谨的学科。这一过程涉及到对极限、连续性及收敛性的深入研究。
三、微积分的基本定理
基本定理是连接导数与定积的重要桥梁,它表明二者之间存在直接关系。这一定理通常被称为“第一基本定理”和“第二基本定理”。
1. 第一基本定理
第一基本定理指出,如果 f 是在 [a, b] 上连续且 F 是 f 的原函数,那么:
F(b) - F(a) = ∫[a,b] f(x)dx
这意味着我们可以通过原函数来计算某一区间内函数值之差,从而求得该区间下方面积。
2. 第二基本定理
第二基本定理则说明,如果 g 是一个可导函数,并且 g'(x)=f(x),那么:
g(b) - g(a) = ∫[a,b] g'(x)dx
这一定理强调了导数与不动点之间密不可分的关系,为解决许多实际问题提供了强有力的方法。
四、微积分在实际生活中的应用
现代社会中,微积分类被广泛应用于科学、工程、经济等多个领域。在这些领域中,它帮助人们解决各种复杂问题,提高效率和准确性。
1. 工程设计
在工程设计中,通过使用导数,可以优化结构设计。例如,在桥梁建造中,通过分析载重情况,可以确定最佳材料和形状,以确保安全性和经济性。
2. 自然科学研究
物理学、生物学等自然科学领域也离不开微积分类。在物理学中,通过运用运动方程,可以预测物体运动轨迹。而在生物学中,通过建立模型,可以模拟种群增长或生态系统动态变化。
3. 财务分析
金融领域同样依赖于微积分类进行数据分析。例如,在投资决策过程中,通过对收益率进行分析,可以评估风险并制定合理策略,从而实现财富增值目标。
五、学习微积分的方法与技巧
掌握好学习方法对于理解和运用好这一复杂理论至关重要。一些有效的方法包括:
1. 理论结合实践
理论知识固然重要,但实践同样不可忽视。通过做大量习题,不仅可以巩固所学知识,还能提高解题能力。建议每天抽出时间进行练习,加深对概念及公式运用的理解。
2. 寻找学习资源
利用网络资源,如视频教程或在线课程,有助于更直观地理解复杂概念。此外,与同伴讨论或参加学习小组,也能促进思维碰撞,加深记忆印象。
3. 定期复习
复习是巩固知识的重要环节,应当制定合理计划,对已掌握内容进行周期性的回顾。同时,要及时查漏补缺,将不明白的问题记录下来,以便后续查找答案或请教老师。同样也要保持积极心态,相信自己能够掌握这一困难但充满挑战性的科目。
常见问题解答Q&A
什么是导数?
导数是描述一个函数随自变量变化速率的重要工具,它表示某一点上切线斜率,即该点处函数值随输入值变化而改变程度的一种量度。通过求解导数,我们能够了解函数行为及其图像特征,比如最大值或最小值的位置等信息。
如何理解不连续性?
不连续性指的是当自变量趋向某一点时,函数值没有趋向于该点对应值的一种现象。这可能由于跳跃、不连通或者震荡等原因造成。不连续性的存在会影响到求解极限及整体解析,因此在处理相关问题时需要特别注意这一特征,以及如何利用左极限和右极限来判断不连续类型及性质。
为什么学习微积分类很重要?
学习微积分类不仅能提升逻辑思维能力,还能帮助我们更好地理解自然现象以及社会经济活动背后的规律。在科学技术迅猛发展的今天,无论是在专业学习还是日常生活中,都离不开这一工具,因此掌握它显得尤为重要。