“A-Level数学9231是不是很难?”“IB数学AA HL对理工科申请到底有多重要?”“我应该选AP微积分AB还是BC?”每到暑假,这些关于数学体系选择和备考的疑问就会反复出现在家长和学生的讨论中。
作为国际课程中最具区分度、也最容易“拉开差距”的学科,数学不仅是本科申请的硬性门槛,更是逻辑思维与学习能力的综合体现。
今天我们将系统对比三大数学体系,深入剖析A-Level、AP和IB三大数学体系的特点、难点及备考策略,帮助学生在数学学习道路上做出合适的选择。
三大国际课程体系数学对比
1. A-Level数学:分层模块,专业导向明确
A-Level数学按年级可以分为AS和A2,AS涵盖基础微积分、代数等;A2则是深入拓展。
A-Level数学层级还可以划分为(9709)标准数学和(9231)进阶数学;其中9709是标准A-Level数学课程,适合基础中等学生;9231是进阶课程,适合对数学有较高兴趣和能力的学生。


总体来说,A-Level数学强调推导能力与题目应用,考试内容跨度大,计算细致,对基础与逻辑要求并重。
2. IB数学:理论与应用并重,强调综合能力
IB(DP)数学课程主要分为两类:
- AA(分析与方法):更偏学术理论和抽象思维,适合理工科学生
- AI(应用与解释):强调数学应用和数据分析,适合商科、社科方向
其中AA和AI又划分为SL(Standard Level)与HL(Higher Level两个层级,供不同程度学生选择。课程内容涵盖:
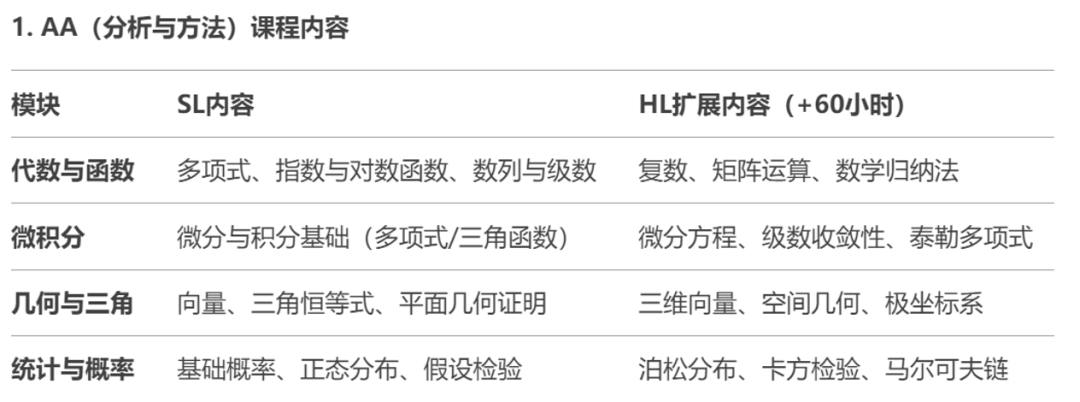
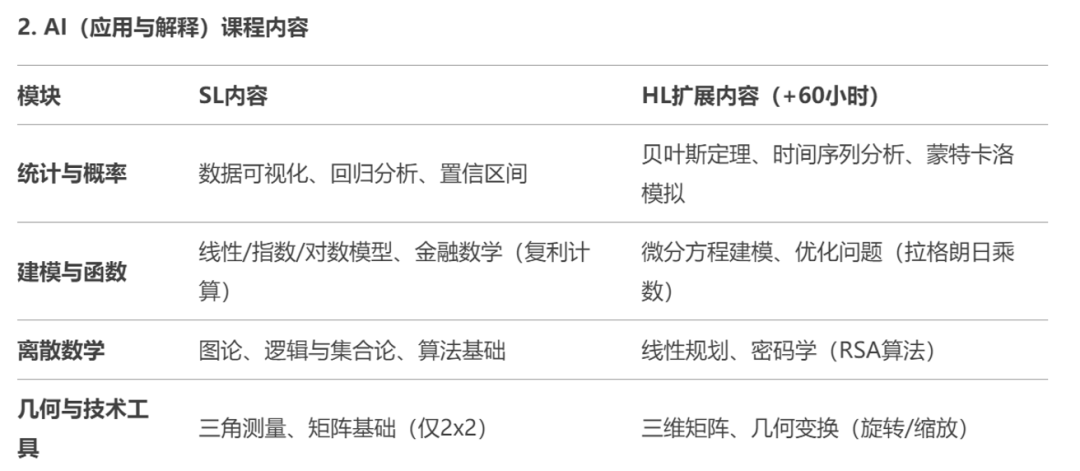
IB数学以笔试+内部评估(IA)的形式进行考核,强调概念理解、建模能力与数学语言表达,整体综合性更强。
3. AP数学:时间短、进度快、知识广
AP数学以“大学先修”为定位,主流方向分为两条:微积分(AB/BC)与统计。其中:
- AP微积分AB:覆盖基础微积分内容,适合大多数学生
- AP微积分BC:涵盖更多章节与进阶概念,知识面更广
- AP统计:偏重文字理解与数据分析,答题逻辑严谨度要求高
微积分AB考试内容:
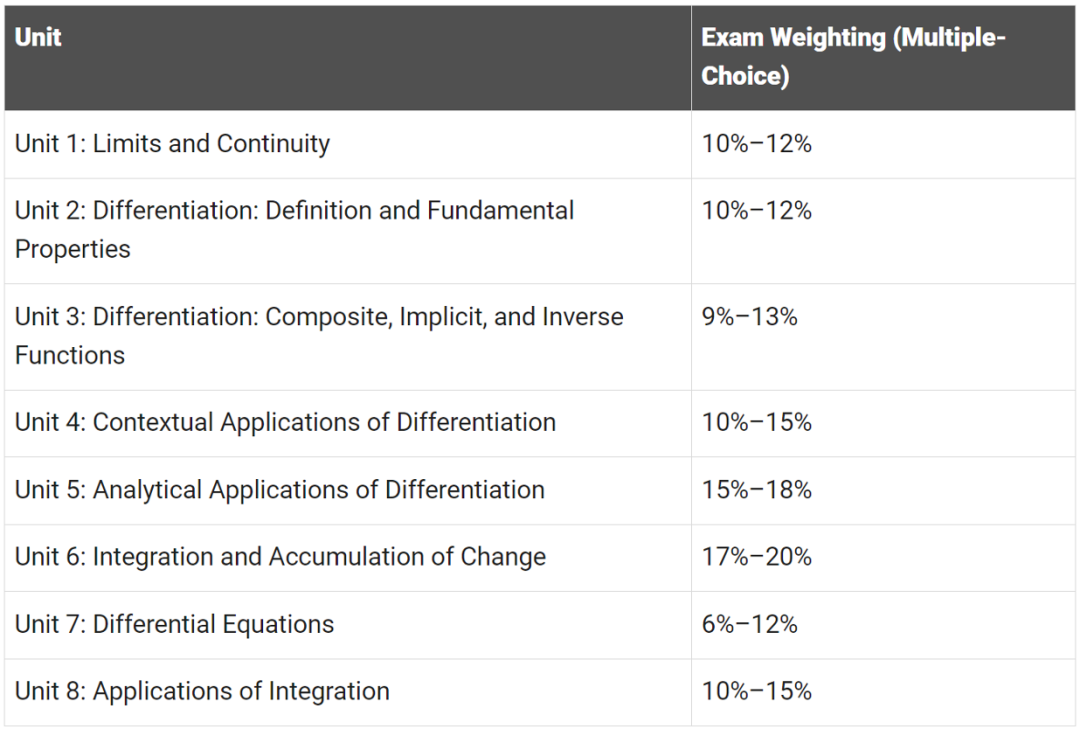
微积分BC考试内容:
AP微积分AB八个单元的所有主题也包含在AP 微积分BC中,另外,AP微积分BC包含两个额外的单元(单元9和10),以及单元6-8中的一些额外主题。

AP统计考试内容:
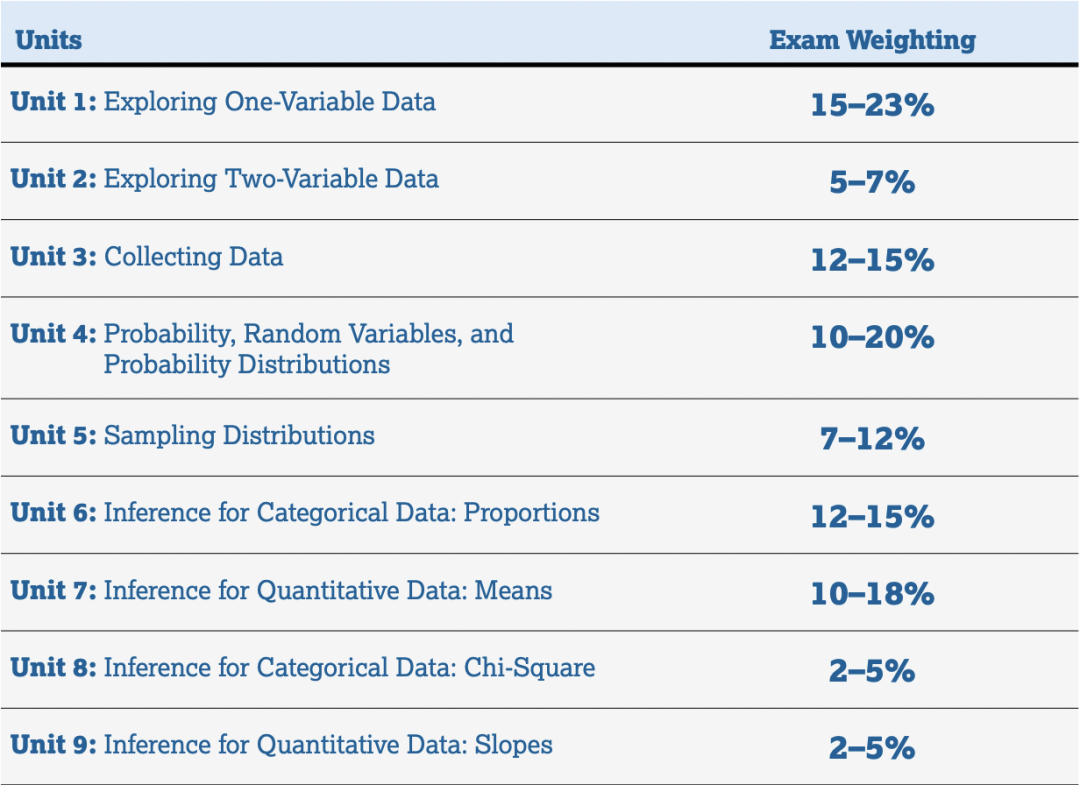
整体而言,AP数学课程需在9月至次年5月间完成学习与备考,时间紧迫,对学生自学能力、预习效率要求极高。
考试难点解析:“理解难+写作难”
在国际课程的三大体系中,真正困住学生的往往不是复杂的计算,而是对概念的深入理解、模型的灵活建立,以及书面表达过程的完整性和严谨性。
1. 微积分难在“深度”而非“广度”
AP微积分虽然知识点分散、考试题量大,但计算难度相对可控,命题套路稳定,核心考点集中在极限、导数、积分及其应用。然而在A-Level和IB体系中,微积分往往涉及更复杂的技巧:
- A-Level Further Math(9231)可能出现二阶微分方程、隐函数微分,以及较为抽象的“以图像、文字描述方式出题的情境建模题”
- IB HL则可能要求对积分原理进行文字推导解释,或在一题中连续处理多种求导与积分技巧,分步考查是否真正理解公式背后的逻辑
🌟结论是:国际课程的微积分不只是“算”,而是“为什么这么算”。
2. “数学写作”门槛高:不是会做就能得分
尤其在IB和A-Level中,考试的“评分标准”远非仅依据答案对错,过程写作和语言表达质量直接决定得分:
- IB数学中,Internal Assessment(IA)是占比20%的写作性项目,要求学生用严谨清晰的文字,解释自己的建模过程与推理逻辑
- A-Level简答题如果没有完整写出推理步骤、单位书写、合理假设说明,即使最终结果正确也可能得不到高分
- AP的FRQ题中,很多学生因没有按格式给出“理由+条件+结论”,导致“答对了也不得分”,尤其在统计、级数、建模推导题目中尤为明显
🌟因此,学生在练题之外,必须培养“数学语言表达能力”,理解什么样的过程描述才是“合格的考试答案”。
3. 情境题建模难,跨章节综合能力要求高
在IB和A-Level中,考试并不满足于单一知识点的考察,而是通过多层小问的情境题,构造真实场景要求学生进行建模、判断并解题:
- IB HL大题中常见“ABCDE五问”,每问递进推进,从模型构建→参数判断→模型优化→结论解释,全面测试学生的综合能力
- A-Level的力学模块题,要求同时调用三角函数、导数、运动模型等多个工具,才能完成“速度-加速度-位移”的建模闭环
- AP微积分中也会出现微分方程模型题,但多局限于“变量可分”的解法,理解难度略低,但情境转换能力依然是失分高发点
🌟难点不是题目多难,而是你是否能跨章节、跨维度,整合工具完成解决。
4. 统计类题目:文字处理+解释能力
统计是很多学生轻视、实则隐藏高难度的模块。以AP Statistics为例:每道FRQ题中,对文字阅读理解与书面表达能力要求极高,很多学生“懂得怎么算”却“写不出怎么解释”。常见失分点包括:
- 没有写出合理的统计假设
- 忽略条件检验(如正态性、独立性)
- 结论写成“常识推理”,没有严格按统计术语表达
🌟不是算对了就能拿分,而是解释得合理、语言够专业、过程完整才是高分关键。
暑期预习怎么做,才真正“有效”?
无论你是准备AP、IB,还是A-Level数学,暑假都是“拉开差距”的绝佳窗口期。然而,“预习”并不是“翻翻书、跟个网课”这么简单。真正有效的暑期预习,既要有方向、有节奏、有深度,也要因体系而异、因人而异。
1. AP数学(微积分/统计)
目标:完成70%以上内容预习
- 建议从Precalculus开始系统性衔接,配合College Board官方真题题型,避免仅做课本练习
- 掌握Desmos等图形计算工具使用
- 统计方向注意术语与写作框架
2. A-Level数学(9709/9231)
目标:建立纯数+力学/统计基础
- 优先建立“概念+技巧+推理”三位一体的框架,熟悉公式背后的推导逻辑
- 建议练习历年Cambridge past papers单元题,并形成错题笔记
- 9231学生可提前接触进一步数学概念如复数、矩阵、二阶微分方程等
3. IB数学(AA/AI)
目标:预习第二年重点单元
- SL学生侧重基础题型复现与图像理解,HL学生需提前接触复杂积分技巧、建模题与统计写作框架
- 建议配合IA选题初探,阅读IA范文以建立“写作感”
- AI方向建议重点训练建模与文字表达,AA方向需重视证明与逻辑推导。
4. 暑期预习的“三步走”方法论
第一步:对照考纲,制定“专题化”学习清单
- 明确所学体系的考纲内容(AP大纲、IB Syllabus、CIE大纲),划分出“已学/未学/薄弱”三类知识点
- 将预习分为“知识构建期”(理解与笔记)+“真题练习期”(应用与强化)两阶段,避免“浅尝辄止”
第二步:练习不止教材,更要“真题同步”
- 很多学生预习仅做教辅题,但真正考试远比教材更灵活
- 建议每学完一个知识点,立刻配合2-3道真题题目练习,逐步建立“知识点-题型”连接
- 特别提醒:IB和AP统计题、A-Level力学题需重点练,避免开学后跟不上
第三步:周期性复习+错误积累
- 预习≠记住,而是提前“建立模型”,后续再复习巩固
- 建议每10天做一次“复盘总结”:整理笔记+再做一遍典型错题
- 重点难点形成“预习错题本”,开学后可以带着问题上课、加速吸收
真正的数学能力不在于考试分数,而在于你是否建立了扎实的知识体系、严谨的思维习惯和持久的学习热情。三大课程虽有差异,但数学的本质相通。这个暑假,或许就是你通往数学高分与学术跃升的起点。