​数学建模中常见的图论问题有哪些？

在前面的推文中，我们了解到，近几年美赛的D题都是与网路关系、网络图有关的，其实这都是数学建模比赛中一类常见的问题——图论问题。下面老师就带大家来了解下什么是图论、有哪些图论问题我们需要关注和解决吧！Gowith me~

什么是图论？

图论起源于一个非常经典的问题——柯尼斯堡（Konigsberg）问题，其本身是应用数学的一部分，直白地来说，如果我们能用点表示某事物，用点与点之间的线表示事物之间的联系，就可以把这件事物抽象地用图的方式表示出来。而运用抽象的方式将问题抽象为图，并为之建立的数学模型，就是图论。

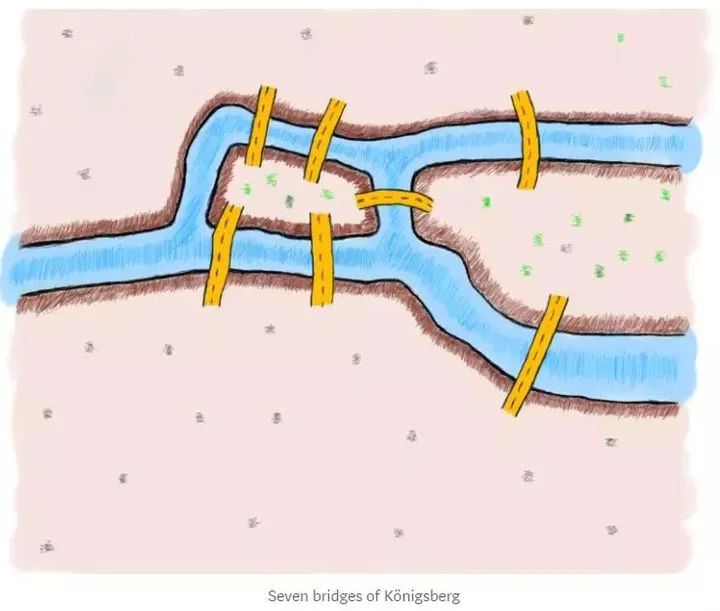
（图源：知乎机器之心https://zhuanlan.zhihu.com/p/34442520）

在数学建模中，图论作为优化问题的一个分支，在各类数学建模比赛中出现频繁，我们不可谓不重视。它是通过优化方法来解决图或网络中出现的各类问题，我们在之前的文章中提到的2019年和2020年美赛的D题均是与图论相关，往年国赛中则主要是集中在B题，如2011年高教社杯全国大学生数学建模竞赛B题“交巡警服务平台的设置与调度”。

数学建模中常见的图论问题

老师分析，数学建模中常见的图论问题主要有三类：最短路径问题、最小生成树问题、（多）旅行商问题，下面老师就依次为大家来介绍一下吧！

01

最短路径问题（SPP）

在老师正式讲解之前，难免有的同学对图的定义和术语不了解，可以先行阅读学习下面的文章（https://zhuanlan.zhihu.com/p/141182838）。

最短路径问题（Shortestpath problem）是图论研究中的一个经典算法问题，旨在寻找图（由结点和路径组成的）中两结点之间的最短路径。最短路径问题根据初始条件的不同，可分为五种情况：

1）最短路径问题：旨在寻找图中两点之间的最短路径；

2）确定起点的最短路径问题：即已知起点，求最短路径的问题；

3）确定终点的最短路径问题：与确定起点的问题相反，该问题是已知终点，求最短路径的问题。在无向图中该问题与确定起点的问题完全等同，在有向图中该问题等同于把所有路径方向反转的确定起点的问题；

4）确定起点终点的最短路径问题，即已知起点和终点，求两点之间的最短路径；

5）：全局最短路径问题：求图中任意两点间的最短路径。也可以合并为一种情况——全局最短路径问题，只要求出全局最短路径，那其余四种情况也已经包含在内了。而计算最短路径的常用算法有迪杰斯特拉算法、贝尔曼-福特算法、弗洛伊德算法等，下面老师将为大家一一介绍其基本概念、优缺点、适用情况和案例分析。

迪杰斯特拉（Dijkstra）算法：用于解决从起点到其他各结点的最短路径，解决的是有向图中最短路径问题。其主要特点是以初始点为中心向外层层扩展，直到扩展到终点为止，但也有图中不能存在负权值的边的限制。

贝尔曼-福特(Bellman–Ford)算法：用于解决从起点到其他各节点的最短距离。与迪杰斯特拉算法不同的是，贝尔曼-福特算法可支持存在负权重的情况，即打破了图中不能存在负权值的边的限制，其边的权值可以为负数、实现简单，但也存在时间复杂度过高的缺点。可对原始算法进行若干优化，提高效率。贝尔曼-福特算法可用于解决以下问题：

1）从A出发是否存在到达各个节点的路径(有计算出值当然就可以到达)；

2）从A出发到达各个节点最短路径(时间最少、或者路径最少等)；3）图中是否存在负环路（权重之和为负数）。

弗洛伊德（Floyd）算法：用于解决任意两结点之间的最短路径，可以正确处理有向图或有负权的有向图（但不可存在负权回路)的最短路径问题。弗洛伊德算法与迪杰斯特拉算法或贝尔曼福特算法相比，能够一次性的求出任意两点之间的最短路径，后两种算法运行一次只能计算出给定的起点和终点之间的最短路径。

当然，弗洛伊德算法计算的时间也要高于后两种算法。对于案例分析，2020年某高校国赛暑期培训赛第五轮的赛题“选址与路线规划问题”问题一中则是明显有解决最短路径问题的需求，让我们一起来分析一下问题一。某城市共有52个居住区域，各居住区域的人口（单位：千人）如下表：

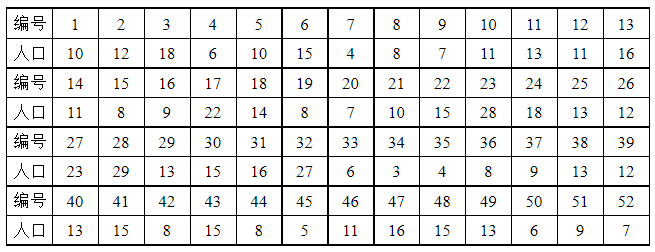
各居住区域的道路连接如下图：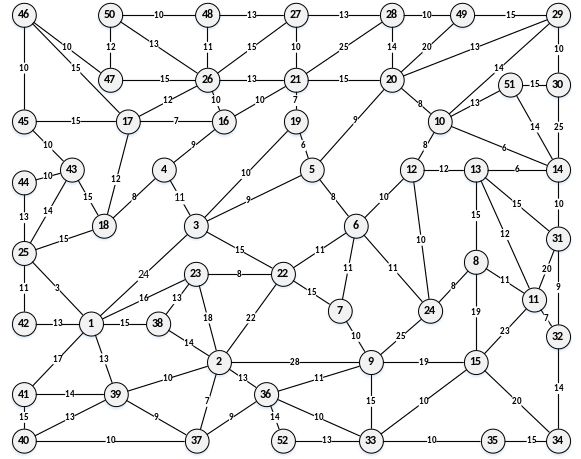

（图源：2020年某高校国赛暑期培训赛第五轮的赛题图）

（注：横线上的数据表示相邻城市之间的距离，单位：百米）

（1）政府拟建3个行政服务站，问分别建在何处才能方便广大市民。问题一要求我们在52个居住区域中，选出3个居住区域并建立能够方便广大市民的行政服务站。

由问题一本身可知，此题为最优选址问题，且无负权回路，比较适合寻求赋权图中任意两点之间最短路径的Folyd算法，而题干中的“方便广大市民”是既要考虑行政服务站与其他居住区域的距离，也要考虑各居住区域的人口，故计算权重时可将两者同时考虑进去，即建立距离（单位：百米）乘以人口（单位：千人）的权重。

同时问题一要求选出3个最优点位置，故需要考虑各点作为行政服务站前提下的人口距离权重情况，即在计算效率能够接受的前提下务必考虑每一种情况，可利用穷举法和Folyd算法计算出各居住区域作为行政服务站与其他区域的人口距离权重，并相互比较选出最小的3个作为最终的行政服务站位置。

接着以3个行政服务站位置为基点，再次利用Folyd算法计算其他居住区域与这3个行政服务站的人口距离权重，并将其他居住区域分别划分至这3个人口距离权重中最小的行政服务站的最佳管理区域中，即可求出各行政服务站的最佳管理区域中的各居住区域。

02、最小生成树问题（MTP）

最小生成树问题（Minimumspanning treeproblem）也是一种常见的图论问题，路线设计、道路规划、官网布局、公交路线、网络设计，都可以转化为最小生成树问题，如要求总线路长度最短、材料最少、成本最低、耗时最小等。

相较于最短路径问题，最小生成树是要保证整个拓扑图的所有路径之和最小，但不能保证任意两点之间是最短路径。在正式了解之前，大家可以先了解如下几个关于最小生成树的概念：

连通图：在无向图中，若任意两个顶点vi与vj都有路径相通，则称该无向图为连通图。

强连通图：在有向图中，若任意两个顶点vi与vj都有路径相通，则称该有向图为强连通图。连通网：在连通图中，若图的边具有一定的意义，每一条边都对应着一个数，称为权；权代表着连接连个顶点的代价，称这种连通图叫做连通网。

生成树：一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边，如果生成树中再添加一条边，则必定成环。

最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。

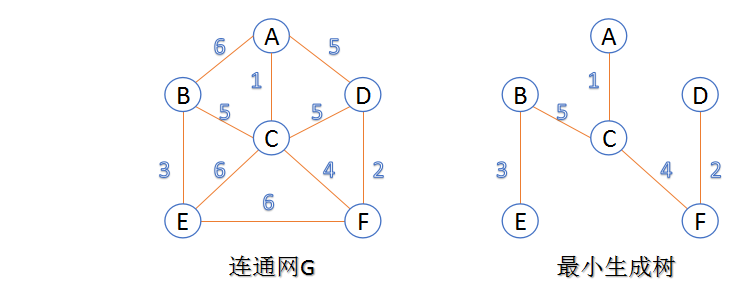
（图源：勿在浮沙筑高台http://blog.csdn.net/luoshixian099/article/details/51908175）

对于最小生成树问题，典型的算法有两种：普里姆（Prims）算法和克鲁斯卡（Kruskal）算法，下面老师将分别为大家介绍两种方法的基本概念、适用情况和案例分析。

普里姆（Prims）算法：以顶点为基础构造最小生成树，每个顶点只与连通图连接一次，因此不用考虑在加入顶点的过程中是否会形成回路。算法从某一个顶点开始，每次选择剩余的代价最小的边所对应的顶点，加入到最小生成树的顶点集合中，逐步扩充直到包含整个连通网的所有顶点，可以称为“加点法”。Prim算法每次选择顶点时，都需要进行排序，但每次都只需要对一部分边进行排序。Prim算法的时间复杂度为O(n*n)，与边的数量无关，适用于边很多的稠密图。

克鲁斯卡（Kruskal）算法：以边为基础构造最小生成树，利用避圈思想，每次找到不使图构成回路的代价最小的边。算法初始边数为0，每次选择一条满足条件的最小代价边，加入到边集合中，逐步扩充直到包含整个生成树，可以称为“加边法”。Kruskal 算法的时间复杂度为O(mlogm)，主要是对边排序的时间复杂度，适用于边较少的稀疏图。

案例分析如下：某市区有7个小区需要铺设天然气管道，各小区的位置及可能的管道路线、费用如图所示，要求设计一个管道铺设路线，使天然气能输送到各个小区，且铺设管道的总费用最小。

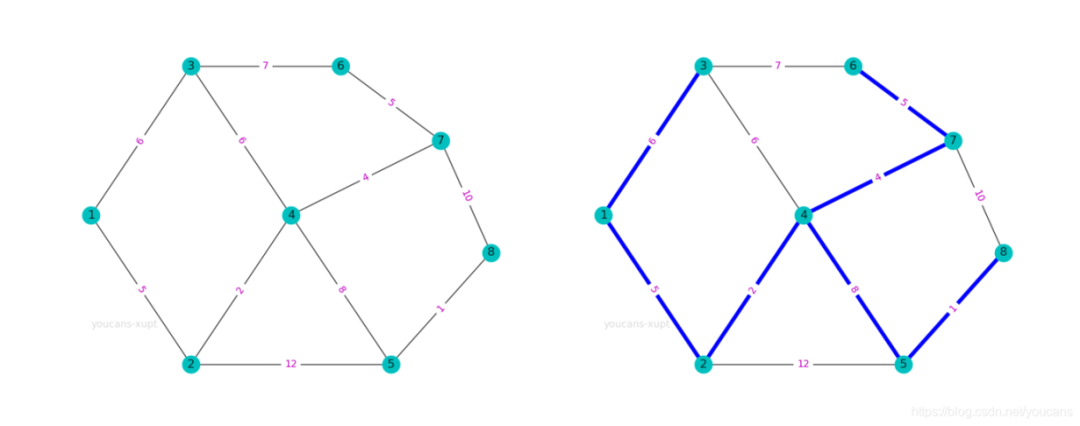（图源：小白YouCanshttps://blog.csdn.net/youcans?type=blog）

老师分析，这是一个典型最小生成树问题，通过上述两种算法即可解决问题，如运用Python平台NetworkX的minimum_spanning_tree()函数即可求出费用最小的管道路线。

03、旅行商问题（TSP）

旅行商问题（TravelingSalesman Problem）是运筹学组合优化领域中一个著名的NPC问题，也是数学建模中一个常见的图论问题，应用领域十分广泛。经典的旅行商问题（TSP）可以描述为：一个商品推销员要去若干个城市推销商品，该推销员从一个城市出发，需要经过所有城市后，回到出发地。

而多旅行商问题（MTSP）可以描述为：多个商品推销员要去若干个城市推销商品，这些推销员最开始都在同一个城市，他们可以被分配到不同路径，在经过所有的城市后，大家都回到出发的城市。对于TSP和MTSP问题，目前为止是不存在多项式算法的。因此当问题规模还比较小时，可以运用传统的运筹学算法，例如分支定界、动态规划等方法求取最优解。

当问题规模大的时候则需要借助一些启发式或者元启发式算法（如模拟退火算法、遗传算法、粒子群算法等等）求取近似最优解。老师继续以2020年某高校国赛暑期培训赛第五轮的赛题“选址与路线规划问题”问题三为例进行分析。

3）近日，该市受到特大暴雨袭击，受灾严重，市领导从市政府所在地（区域6）出发，分三个小组巡视所有区域，了解居民受灾情况，巡视完后返回区域6，假设巡视人员在街道上的行驶速度为30km/h，在每个区域的停留时间为10分钟，问如何规划巡视路线，使巡视效率最大化？对于问题三，要求我们给出对市领导小组巡视的最大巡视效率的巡视路线，从问题三本身可以看出，此为多旅行商问题（MTSP），所要求的巡视效率最大化即是通过最短路径所花费的时间，但与一般的MTSP不同的是，本题中的起点区域6向3外延伸的路径只有5条，也就是所求得的巡视路线中必有重复经过的路径。

同时考虑居住区域的数量等方面，我们选择较传统算法对求解MTSP尤其是上述两点有着更高效率的启发式算法——遗传算法。首先进行遗传编码，设置染色体基因型为两段：

一是路径基因型，用来记录各小组的最短巡视路径；

二是中断点基因型，用来分割效率最大化前提下不同小组的最短巡视路径。接着结合问题参考相关文献选择合适的种群规模和迭代次数，随后选择相应的适应度函数。

针对选择算子，使用轮盘赌选择的方法，即每一个个体被选择的概率就等于它的适应值与整个种群中个体适应值和的比例；针对交叉算子，染色体交叉采用基于路径表示的部分匹配交叉、顺序交叉、循环交叉三种交叉混合方法，以提高子代继承父代优良特性的可能性，加快算法的搜索速度；针对变异算子，采用交换变异法，即任选序号交换插入的方法。在结束迭代次数之后，即可得到各小组的可达路径矩阵，即效率最大化前提下的巡视路线（如下图）。

接着结合问题一Floyd算法计算得到的距离矩阵，进行矩阵点乘，即可计算出各小组所走路程总和，进而求解出各小组巡视路线所花费的时间，即巡视效率。

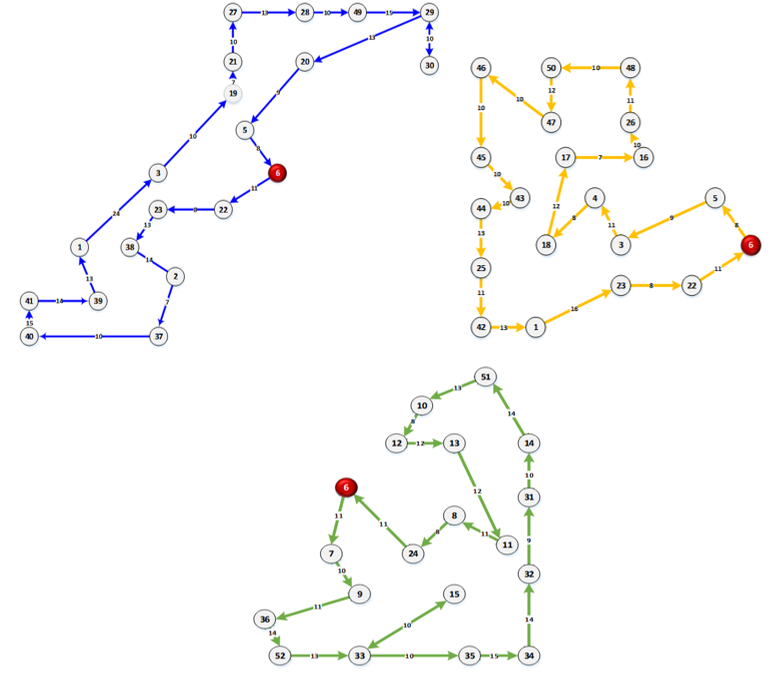
今天老师初步地带大家介绍了下图论的相关概念，以及数学建模中常见的三大图论问题和相应解决措施，想必大家一定迫不及待地想进行深入学习了。