应用数学课题项目回顾：数学模型解密博弈胜负与双赢

我们将带你“云体验”为期七周的线上科研项目，跟随大牛教授学习，在博士导师的辅导下，完成科研课题并撰写科研论文的全过程。

#01 项目介绍

项目介绍：

学生将在项目中学习博弈论的核心，比如正则形式博弈、扩展形式博弈、占优策略等，同时活学活用，解决现实问题。博弈指在一定游戏规则约束下，基于相互作用的环境条件，各游戏参与方依据所掌握的信息，选择各自策略和行动，以实现利益最大化和风险成本最小的过程。本课题将主要集中在西方文化体系下博弈（Game）的理论和概念，例如纳什均衡理论。博弈论（Game Theory）属应用数学理论，通常应用于经济学领域。

商业决策者借助数学方法进行经济博弈。纳什均衡是博弈论中的重要理论，又称完全信息静态博弈，奠定了现代主流博弈理论的基础。本项目也将研究纳什均衡的概念、理论和现实应用。同时我们也会讨论子博弈精炼纳什均衡。子博弈精炼纳什均衡是对纳什均衡的补足，“要求参与者在任何时间和地点的决策都是最优的”。

项目大纲：

·什么是博弈论？What is Game Theory

·纳什均衡理论 Nash Equilibrium

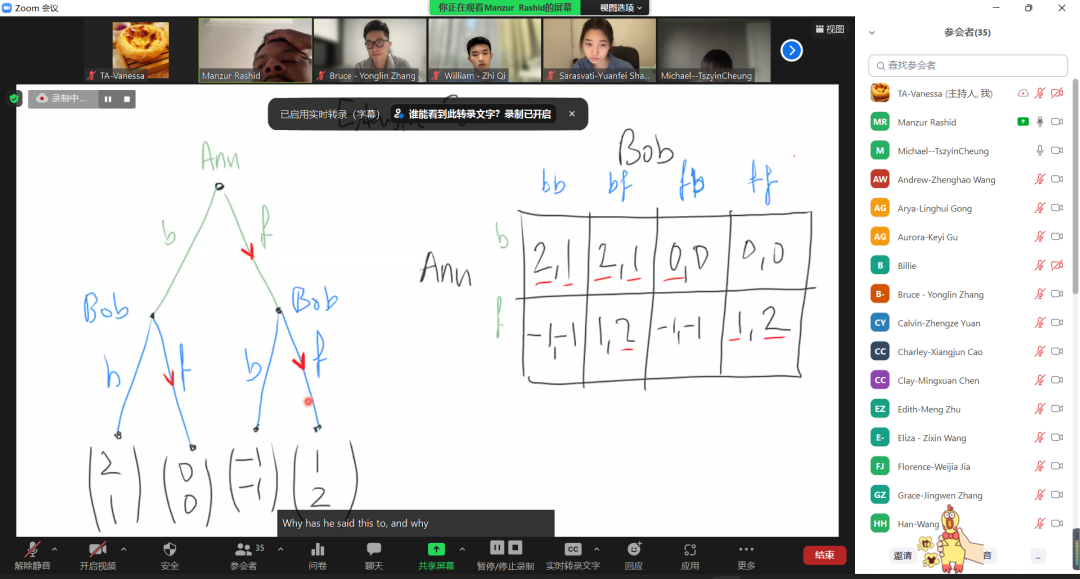
·博弈论衍生理论分析 Extensive Form Games、Backward Induction、Subgame Perfect、Equilibrium

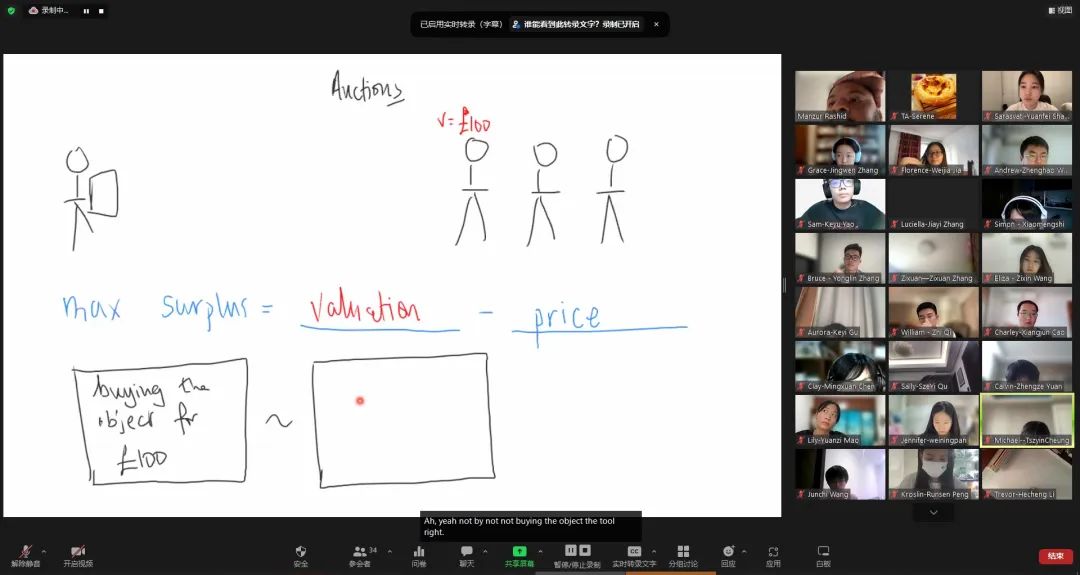
·拍卖模拟实践1 Auctions I

·拍卖模拟实践2 Auctions II

·项目回顾与成果展示 Program Review and Presentation

·论文辅导 Project Deliverables Tutoring

#02 导师介绍

导师：Manzur

伦敦大学学院 University College London (UCL)

终身教授

Manzur导师现任伦敦大学学院（UCL）经济学终身教授，曾任教于世界著名学府剑桥大学和伦敦政经学院。他取得了UCL经济理论博士学位，关注博弈论、有限理性与产业组织研究，并且在世界著名的剑桥大学三一学院以极为优异的成绩取得了经济学本科学位和哲学硕士学位。Manzur导师著有Macroeconomics for Dummies一书，深入浅出地讲解宏观经济学，同时在SSCI期刊Economic Theory发表论文探讨伯特兰德（Bertrand）价格竞争模型。导师出众的学术研究能力更是获得了业内知名组织和企业的认可和青睐。

#03 项目进行中

导师、副导师与助教的教学以及班主任的全程陪伴，充分保证学员的项目学习过程以及体验，提高项目学习的效果。

课堂截图

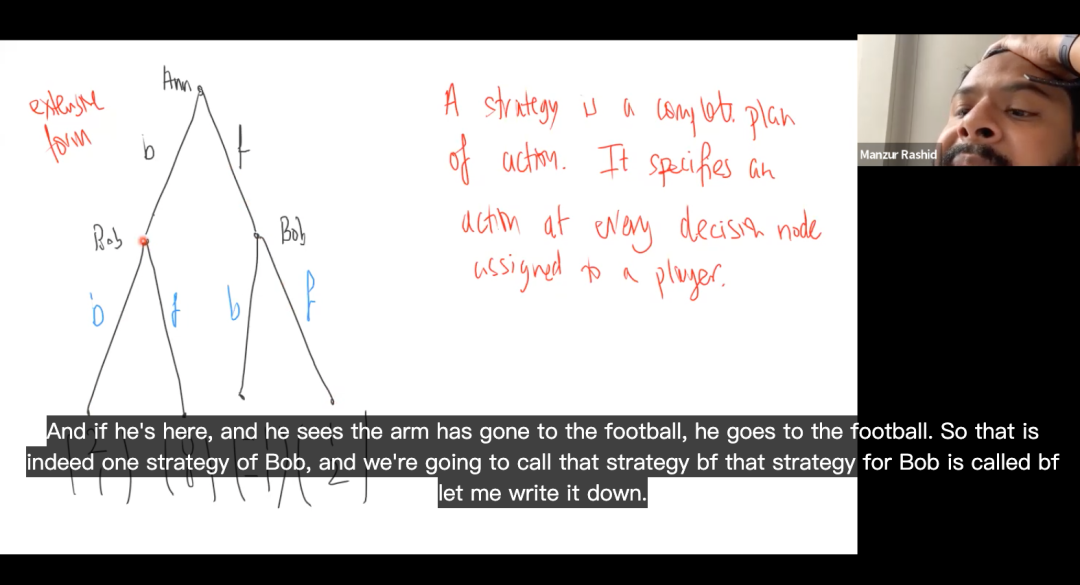
#04 项目成果展示

在科研小组成员的共同努力以及导师和班主任团队的指导帮助下，学员将自主完成完整的项目，并最终向导师进行汇报。

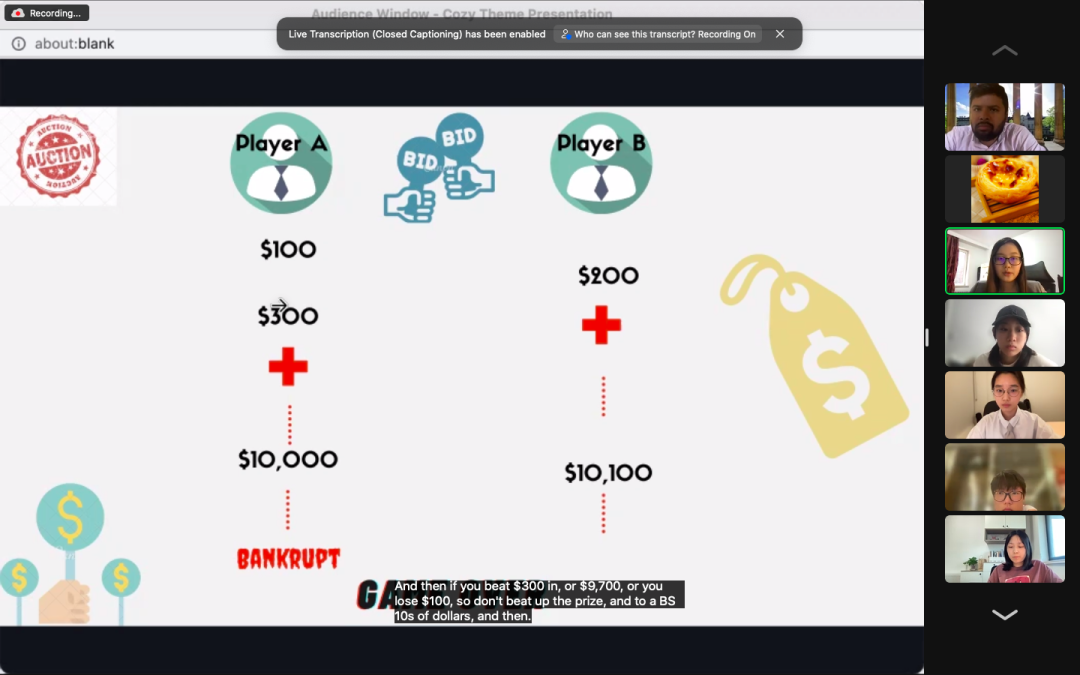
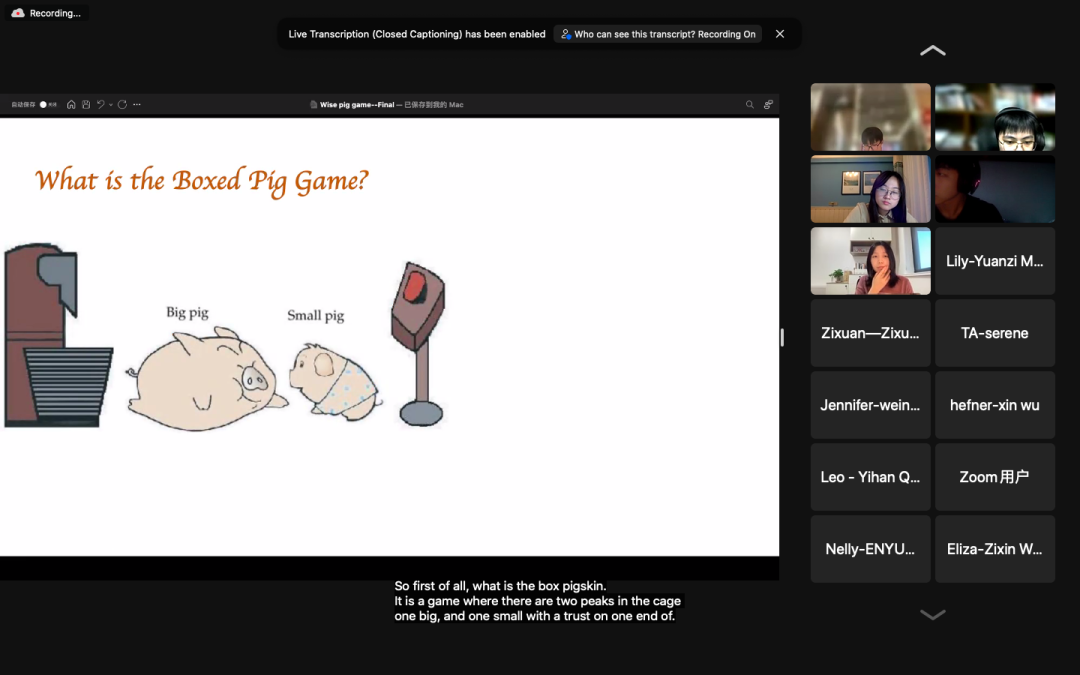
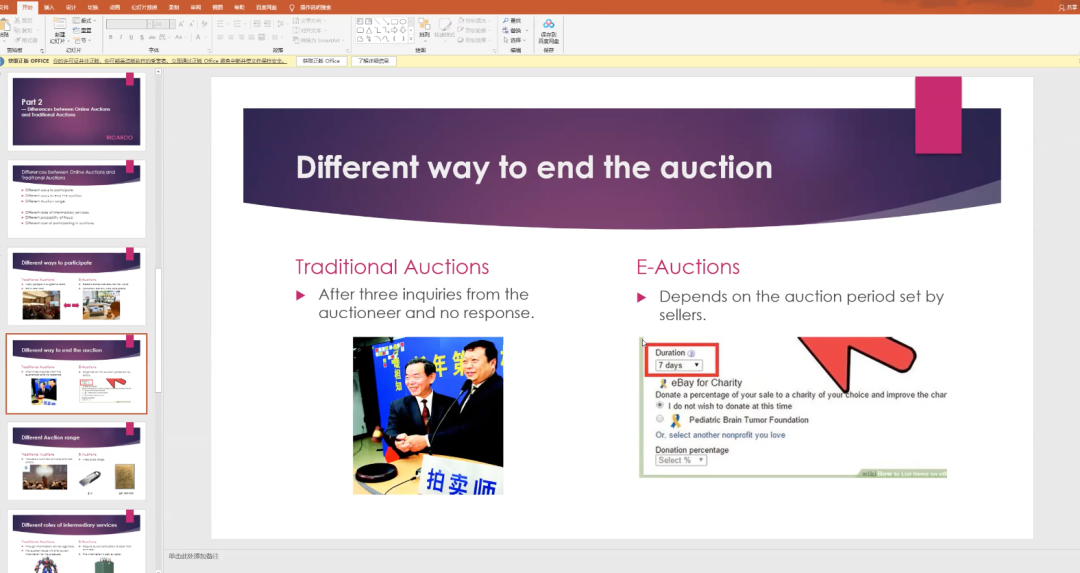
小组作业展示

同时，在学术写作课程结束后，写作老师将安排论文定题课。配合论文辅导团队的指导，学生将会把小组的科研成果进一步精细打磨，形成高质量的科研成果产出。

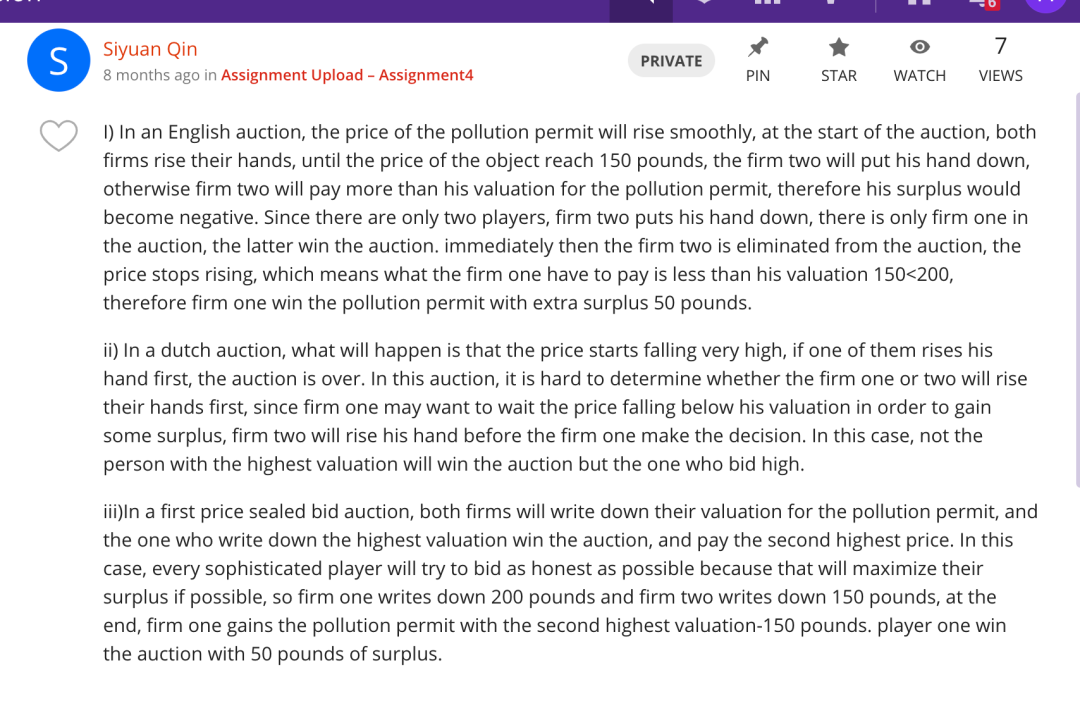
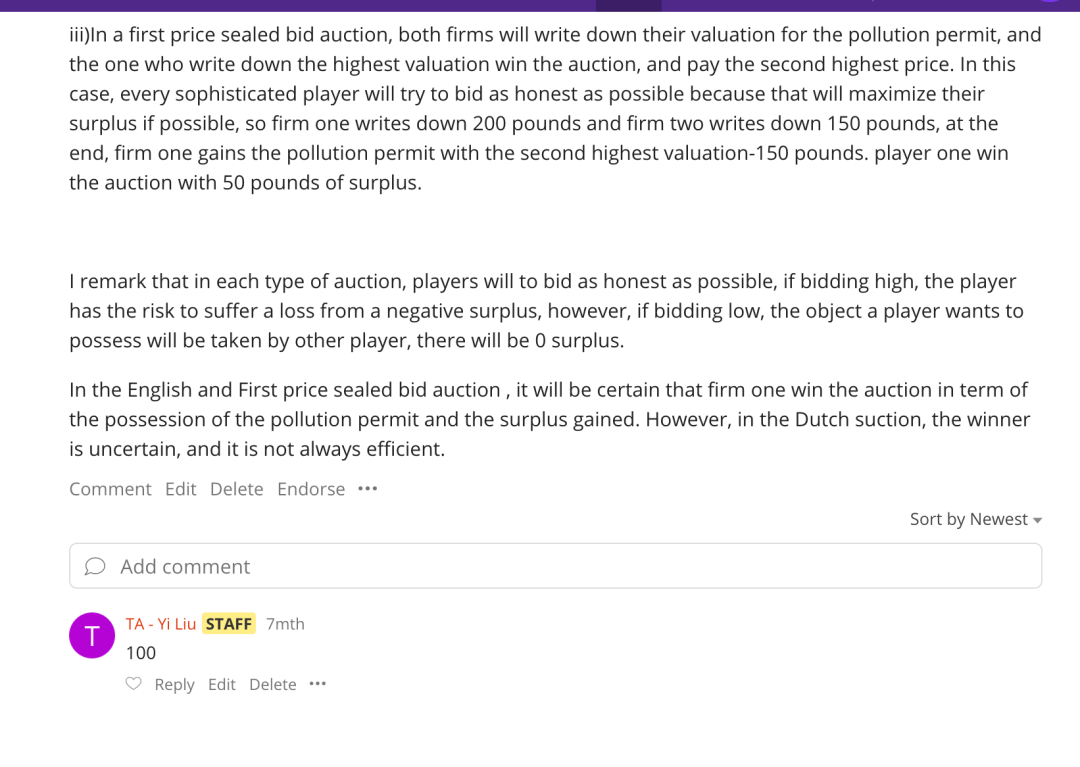
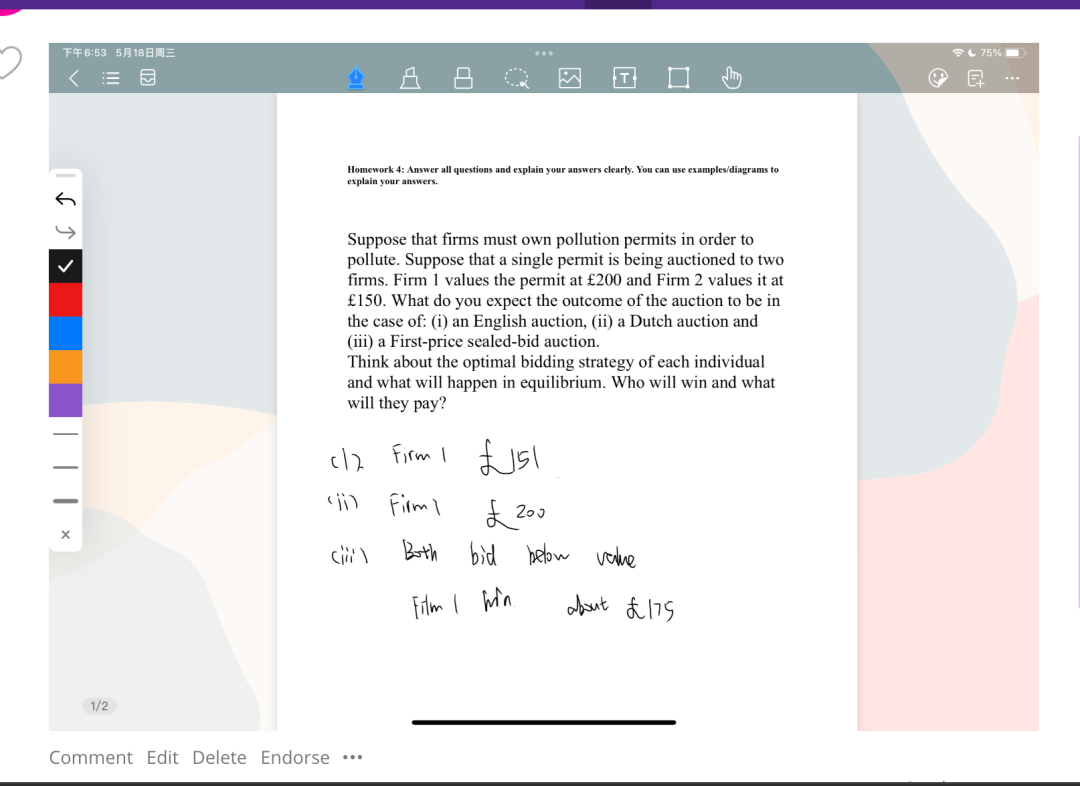
#05 学员反馈

·论文老师沟通