各位备战爱德思P3的同学们,大家好!夏季大考在即,我们为大家精心准备了2024年最新的P3真题逐题解析。接下来,我们会把每道题的题目、官方答案都清晰呈现,并附上针对性的点评和复习要点,希望能帮助大家高效梳理知识,精准把握考向,为P3考试做好最后的冲刺。

Q1


老师点评:这P3的第一题,可以说是一道非常简单且经典的开场题,主要考察的就是三角恒等变换。核心考点与策略:题目给出了包含tan²θ 和 secθ 的方程。
看到这种形式,我们的第一反应就是要利用核心的三角恒等式 1 + tan²θ = sec²θ (或其变体 tan²θ = sec²θ - 1),将方程中的所有三角函数统一成一种。在这道题里,我们选择将 tan²θ 替换掉,从而得到一个关于 secθ 的方程。
解题步骤:代入恒等式后,方程会化为一个标准的一元二次方程(in terms of secθ)。解这个二次方程,会得到secθ 的两个可能值。将secθ 转换为 cosθ (因为 cosθ = 1/secθ) 以便进一步求解角度。
关键注意事项:
解的有效性:在得到cosθ 的值后,务必检查其是否在 -1 ≤ cosθ ≤ 1 的范围内。比如本题中,secθ = 2/3 导致 cosθ = 3/2,这个值超出了范围,因此没有实数解 (no real solutions),这个分支就不需要继续了。
多解性:对于有效的cosθ 值(本题是 cosθ = -1/3),在给定的角度范围 (0 < θ ≤ 360°) 内,通常会有多个角度解。需要利用计算器和对三角函数图像/CAST图的理解来找出所有符合条件的 θ。
总的来说,这道题的思路清晰直接:恒等变换→ 化为单一函数的二次方程 → 解二次方程 → 考虑解的有效性 → 在指定范围内求解所有角度。只要基础扎实,计算细心,拿分不难。
Q2


老师点评:
(a)小问 - 核心技巧:这道题在(a)小问,其实核心技巧就一个:很多同学看到求dy/dx,可能会想直接对 x = 2y² + 5y - 6 进行隐函数微分,这当然可行,但会稍微麻烦一些。题目给的是x 关于 y 的函数 (x = f(y)),所以更直接、更简单的方法是先求 dx/dy。dx/dy很容易得到是 4y + 5。然后利用关键关系:dy/dx = 1 / (dx/dy),就能轻松得到dy/dx = 1 / (4y + 5)。
这个“先对x 关于 y 求导,再取倒数”的思路,在处理 x=f(y) 形式的微分时非常实用且高效。
(b)小问 - 特殊切线条件:至于(b)小问,它说点P的切线平行于y轴(parallel to the y-axis)。
大家要立刻反应过来:切线平行于y轴,意味着这是一条垂直切线(vertical tangent)。垂直切线的斜率dy/dx 是未定义的 (undefined)。而我们从(a)问知道dy/dx = 1 / (dx/dy)。要使这个分式未定义,它的分母 dx/dy 就必须等于零。
所以,解题的关键就是令(a)问中得到的 dx/dy = 4y + 5 等于零。即4y + 5 = 0。解出y 的值后,再代回原曲线方程就能求出对应的 x 值,从而得到P点坐标。
总的来说,这道题不算难题,但考察了大家对微分方法灵活选择的能力,以及对特殊切线(垂直切线)条件的理解和应用。记住,当曲线方程是x=f(y) 的形式时,求 dy/dx 通常先求 dx/dy 再取倒数会更便捷。
Q3
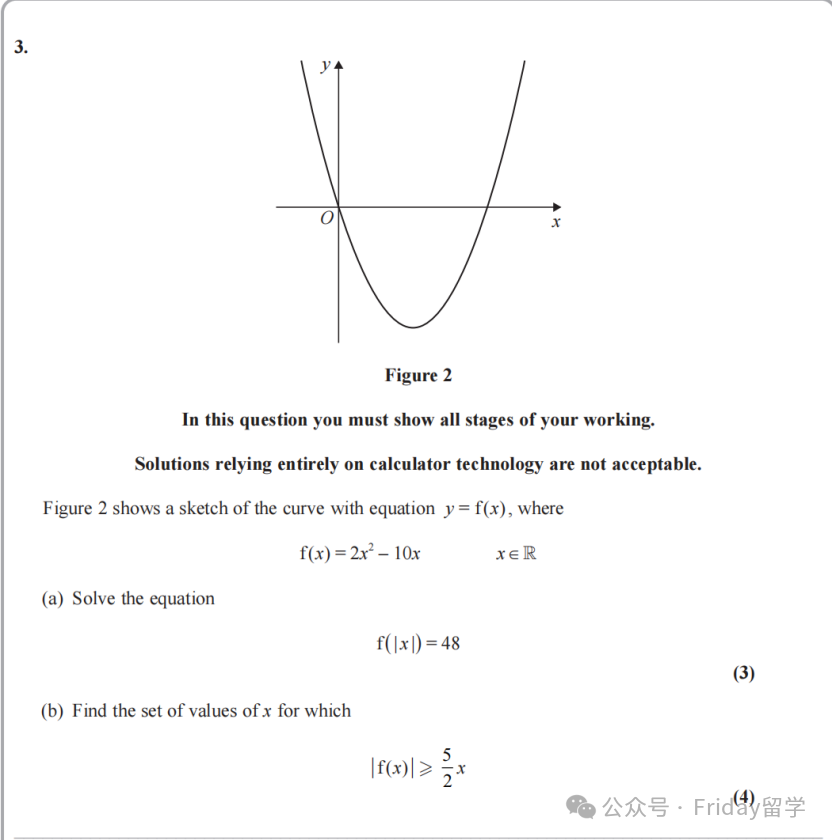
老师点评:这道题的关键点在于处理两种不同形式的带有绝对值的函数。
(a)小问 - f(|x|) 的情况 (绝对值在自变量上):当绝对值作用在自变量x 上,即 f(|x|) 时,其核心特性是:无论 x 取正值还是负值,只要它们的绝对值相同(例如 x=2 和 x=-2),代入 f(|x|) 后得到的函数值是一样的。这直接导致了y = f(|x|) 的图像是关于y轴对称的 (symmetrical about the y-axis)。
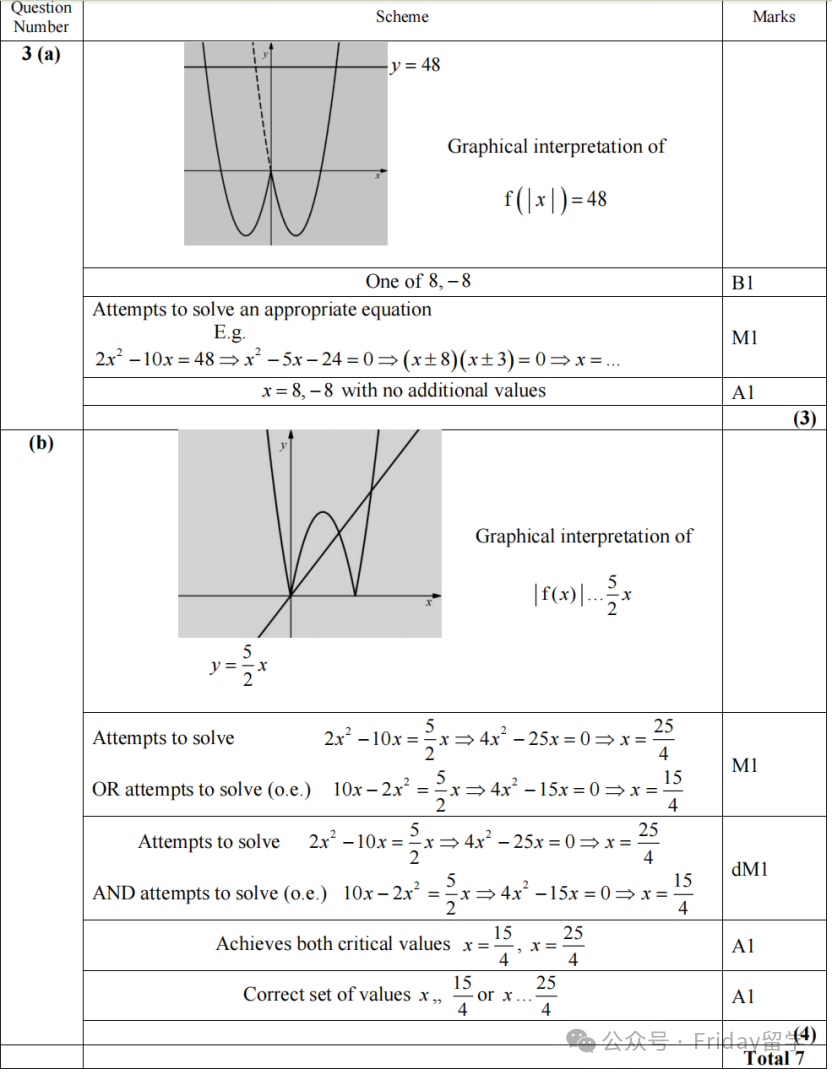
在画图或者理解图像时,一个便捷的方法是:先画出y = f(x) 在 x ≥ 0 (即y轴右侧) 的部分,然后将这部分图像直接关于y轴对称地“复制”到 x < 0 (即y轴左侧) 的部分,就得到了 y = f(|x|) 的完整图像(正如题目图(a)所示)。解方程f(|x|) = 48 时,可以令 y = |x| (其中 y ≥ 0),代入原方程得到一个关于 y 的二次方程,解出 y 后再反解 x,注意舍去不符合 y ≥ 0 的解。
(b)小问 - |f(x)| 的情况 (绝对值在整个函数表达式外):当绝对值作用在整个函数表达式f(x) 外,即 |f(x)| 时,其核心特性是:函数值 |f(x)| 永远是非负的。
这导致了y = |f(x)| 的图像变换规则是:将 y = f(x) 图像中所有在 x轴下方 (即 f(x) < 0 的部分) 关于x轴对称地翻折到x轴上方,而原本在x轴及上方的部分保持不变(正如题目图(b)所示)。在解方程|f(x)| = (5/2)x 时,一个重要的前提是右侧的 (5/2)x 也必须大于等于零,即 x ≥ 0。
然后,我们可以分两种情况讨论:f(x) = (5/2)x (当f(x) ≥ 0 时)-f(x) = (5/2)x (当f(x) < 0 时)分别求解这两种情况,并结合x ≥ 0 和各自情况下 f(x) 的符号条件来检验解的有效性。
结合图像理解(b) 问:解|f(x)| = (5/2)x 实际上就是在找曲线 y = |f(x)| 与直线 y = (5/2)x 的交点。从图像(图(b)) 上可以很直观地看到交点情况。例如,直线 y = (5/2)x 是一条过原点、斜率为正的直线。
通过观察它与 y = |f(x)| 图像的相交情况,可以预判解的个数,并帮助理解代数解的来源(哪个解对应哪段曲线与直线的相交)。重点是要找全所有的交点,不要因为只考虑了 f(x) 的某一段而遗漏解,导致扣分。
总的来说,准确理解这两种绝对值函数的图像变换是核心,然后结合代数方法(分情况讨论、解二次方程)和图像直观性来求解,并注意检验解的有效性。
Q4


老师点评:这道题是一个非常经典的指数/对数增长模型应用题。这类模型在P3中很常见,比如人口增长、种群数量变化、放射性衰变,或者像本题中的细菌增长。解题时,首先要看清楚是哪个量随哪个量变化,这里是细菌数量N 随时间 t 变化。
(a)小问 - 初始条件:“Initial”(初始)这个词是高频考点,它明确指向t = 0 的时刻。无论是求初始细菌数、初始种群、还是像药代动力学中血液初始药物浓度,都是一个意思。
将 t=0 代入模型,本题就变为解 log₁₀N = 2,考察的是对数形式到指数形式的基本转换 (logₐb = c <=> a^c = b)。(b)小问 - 模型形式转换与运算法则:这一问要求将对数模型log₁₀N = 0.35t + 2 转换为指数模型 N = ab^t。
核心步骤是:先将对数形式化为指数形式:N = 10^(0.35t + 2)。然后熟练运用指数运算法则:x^(m+n) = x^m * x^n和 x^(mn) = (x^m)^n。即N = 10^(0.35t) * 10² = 100 * (10^0.35)^t。对比N = ab^t,就能得到 a = 100 和 b = 10^0.35。
计算b 的值时,注意按题目要求保留有效数字或小数位数。
(c)小问 - 增长率与微分:在指数和对数模型中,经常会结合微积分来考察变化率(rate of change),比如本题的“增长率 (rate of growth)”。“增长率”指的就是N 对 t 的导数,即 dN/dt。
因为(b) 问已经得到了 N 关于 t 的指数函数表达式 N = ab^t(或 N = 100 * (10^0.35)^t),我们直接对这个表达式进行微分。记住指数函数 y = ck^t 的导数是 y' = ck^t * ln(k)。微分后,将题目给定的特定时间(本题是t = 5 小时)代入 dN/dt 的表达式,用计算器算出结果即可。
特别提醒:很多同学容易误以为“增长率”是一个固定不变的值。但在这个指数模型中,增长率dN/dt 本身也是随时间 t 变化的 (因为它通常还包含 b^t 这一项)。
所以题目一定会指定一个特定的时间点来求解瞬时增长率。总的来说,这类题目综合考察了对数与指数的互换、运算法则、模型参数理解以及微分求变化率。关键在于理解概念,熟练公式,细心计算。
Q5

 老师点评:这道题是一道比较经典的P3三角恒等式证明与三角方程求解相结合的题目。
老师点评:这道题是一道比较经典的P3三角恒等式证明与三角方程求解相结合的题目。
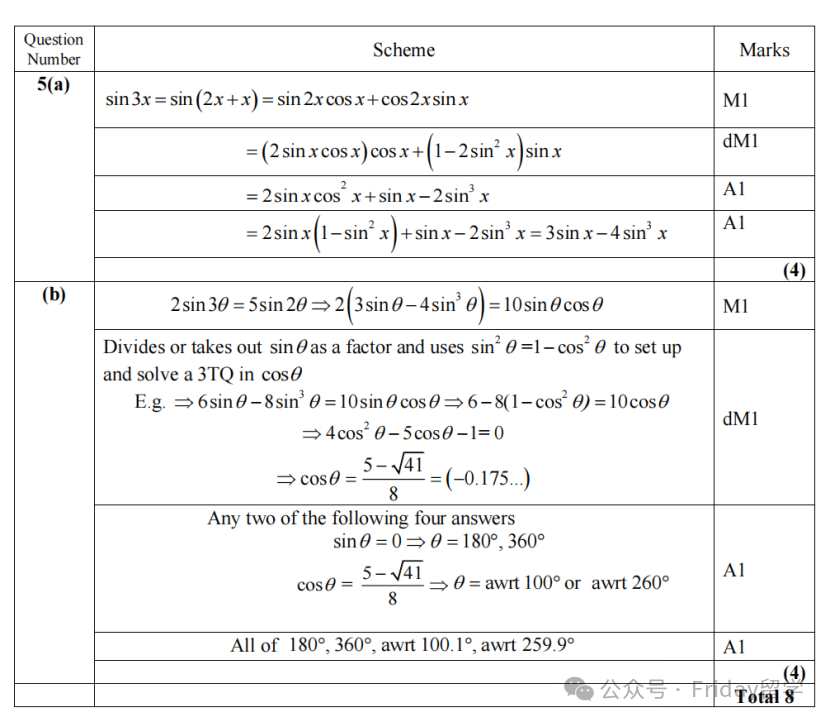
(a)小问 - 证明 sin(3x) ≡ 3sin(x) - 4sin³(x):证明这类三倍角公式,常规思路是拆分角度(3x = 2x + x),然后综合运用和角公式 (sin(A+B)) 和二倍角公式 (sin(2x), cos(2x))。
关键在于,当处理 cos(2x) 时,要根据最终目标(只含 sin(x))选择合适的二倍角形式(如 1 - 2sin²(x)),并利用 cos²(x) = 1 - sin²(x) 来统一所有项,最终化简得到目标恒等式。(核心公式:sin(A+B), sin(2x), cos(2x) = 1 - 2sin²(x), sin²(x) + cos²(x) = 1)(b)小问 - 求解方程 8sin³(x) - 6sin(x) + √3 = 0:P3的题目设计往往环环相扣,(b)问通常能巧妙运用(a)问的结论。
联系与代换:观察方程8sin³(x) - 6sin(x) + √3 = 0,可以发现它与(a)问的 sin(3x) = 3sin(x) - 4sin³(x) 结构相似。
通过提取 -2,原方程可化为 -2(3sin(x) - 4sin³(x)) + √3 = 0。代入(a)的结论,方程即简化为 -2sin(3x) + √3 = 0,从而得到 sin(3x) = √3 / 2。
求解基础三角方程:解sin(3x) = √3 / 2。首先找到主值(如 3x = 60° 或 π/3)。
然后,考虑到 sin 函数的周期性和对称性,在题目给定的 x 的定义域内(例如 0 ≤ x < 360°,则 0 ≤ 3x < 1080°),找出所有满足条件的 3x 的值,最后再将这些值除以3,得到所有 x 的解。
这里我要特别提醒大家一个重要的解题策略:虽然本题通过代换直接解决,但普遍来说,如果在解三角方程时,遇到形如Acos²(x) + Bcos(x) + C = 0 的情况(即包含一次项 cos(x) 的二次型),就应以 cos(x) 为变量求解。
强行将一次项 cos(x) 转换为 sin(x) 相关项通常会使问题复杂化。一次项的三角函数形式,往往决定了我们应该以哪个三角函数为主导变量进行求解。答案呈现:最后,按题目要求保留小数位数,并建议将解按从小到大的顺序排列。
总的来说,(a)问是基础的恒等式推导,(b)问则考察如何利用已知结论简化问题,并正确求解三角方程。同时,上面提到的关于如何处理混合三角函数一次项的策略非常关键,是大家解题时的重要考量。
同学们可以看到,P3的题目综合性更强,对知识点的灵活运用要求也更高。考虑到篇幅,今天的精讲就先到这里,作为上半部分的内容。一张完整的P3试卷通常包含九道大题,希望上半部分的讲解能帮助大家更好地理解考点,查漏补缺。我们下半部分再见!