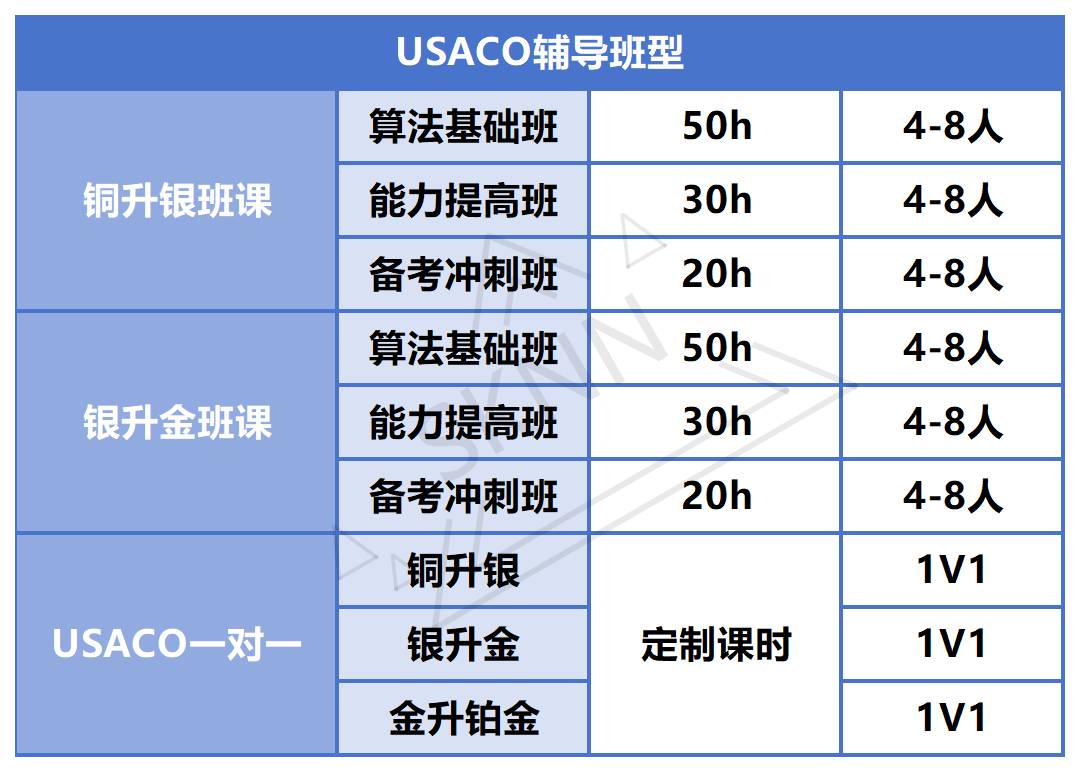
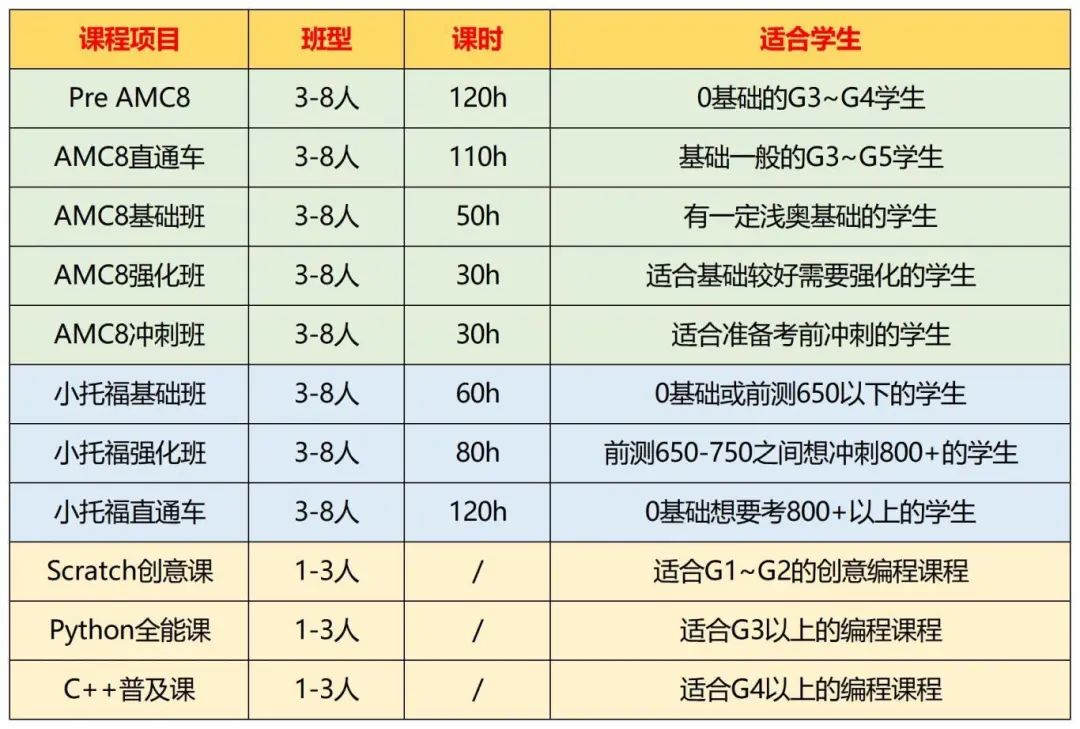
A-Level数学涵盖内容广泛,知识点复杂,到底应该怎么学?
十月大考在即,本文深入剖析A-Level数学的重要考点,并归纳整理了完整版的A-Level数学知识点手册。
A-Level数学的架构
首先需要搞清楚的是A-Level 数学主要的四大模块:纯数学、统计数学、机械数学以及决策数学。
其中,纯数学的 4 个单元(P1、P2、P3、P4)是必选,另外 2 个单元则需在剩余的统计、机械、决策数学单元(S1、S2、M1、M2、D1)中任选其二。
AS 阶段,学生需修读 P1+P2,再从 M1、S1、D1 中选其一;A2 阶段,必修 P3+P4,然后选择一个在 AS 阶段未修的单元。
A-Level 数学的四大模块各有侧重,学习时需根据难度和分值占比合理分配精力:
🌱纯数学(60%+ 分值,优先级最高)
作为基础中的基础,纯数学的知识点贯穿整个课程,必须筑牢根基:
函数与图像:
一次、二次、三角函数、指数对数函数是高频考点。
学习时要结合图像记性质,比如二次函数的顶点坐标、对称轴与最值的关系,三角函数的周期、奇偶性与图像平移规律。
建议用 “列表法” 对比不同函数的定义域、值域和单调性,避免混淆。
微积分:
求导(复合函数、隐函数)和积分(换元、分部)是核心运算,占纯数近 40% 分值。
初学者可从 “物理意义” 切入 —— 导数是瞬时变化率(如切线斜率),积分是累积效应(如面积计算),再通过 “题海 + 错题本” 强化运算熟练度。
数列与向量:
等差数列、等比数列的通项公式和求和公式要 “知其然更知其所以然”,比如等比数列求和公式推导中 “错位相减法” 的逻辑;
向量的点乘、叉乘运算需结合几何意义(如夹角计算、平行垂直判定),三维向量可借助空间坐标系辅助理解。
🌱 统计数学(选考热门,优先级次高)
统计对逻辑思维要求高,需注重 “从数据到结论” 的推导过程:
S1 重点:
概率计算(条件概率、独立事件)和正态分布是得分关键。
学习概率时,用 “树状图” 梳理多步骤事件,避免遗漏情况;
正态分布要牢记 “3σ 原则”,会用标准化公式(Z=(X-μ)/σ)转化非标准正态分布问题。
S2 难点:
假设检验(Hypothesis Testing)是很多同学的 “绊脚石”。
记住 “三步走”:
明确原假设与备择假设→选择检验统计量(如 t 检验、Z 检验)→根据显著性水平判断是否拒绝原假设。
建议结合实际案例(如 “新药疗效是否显著”)理解逻辑,而非死记公式。
🌱 机械数学(偏物理思维,优先级中等)
机械数学需要 “数学 + 物理” 双重视角:
M1 核心:
牛顿运动定律和动量守恒是基础。
分析受力时画 “受力分析图” 是必做步骤,尤其注意摩擦力的方向与大小计算;
匀变速直线运动的三大公式(v=u+at、s=ut+½at²、v²=u²+2as)要能灵活变形,结合图像(v-t 图面积表位移)辅助解题。
M2 进阶:
抛体运动可分解为水平匀速和竖直自由落体运动,用三角函数拆分初速度;
能量守恒定律(动能 + 势能 = 恒量)常用来简化复杂运动问题,比直接用牛顿定律更高效。
🌱 决策数学(部分考试局,优先级较低)
以算法和优化为主,适合逻辑清晰的同学:
重点掌握最短路径算法(Dijkstra) 和线性规划,解题时按 “步骤模板” 操作(如线性规划先画可行域,再找目标函数最优解),难度较低但需细心。
掌握 “怎么学”:高分实战方法论
1. 概念理解:从 “记公式” 到 “懂逻辑”
A-Level 数学很少直接考察公式背诵,而是侧重应用。
比如学习二项式定理时,不仅要记住展开式,还要理解其 “组合意义”(从 n 个元素中选 k 个的方式数),这样才能应对 “求特定项系数”“近似计算” 等变式题。
建议用 “费曼学习法”—— 把知识点讲给他人听,能讲清楚才是真懂。
2. 刷题策略:分阶段针对性突破
基础期(知识点刚学完):
做教材课后题,确保每个考点覆盖到,重点练 “步骤规范性”(如积分需加常数 C,概率计算要写清事件定义)。
强化期(模块复习阶段):
刷近 5 年真题,按 “题型分类” 刷题(如集中攻克 “三角函数图像变换”“定积分求面积”),总结每种题型的解题套路。
冲刺期(考前 1 个月):
掐时间做整套真题,模拟考试状态,重点分析 “重复出错的知识点”,用 “错题归因表” 记录错误类型(如公式记错、计算失误、题意理解偏差)。
3. 工具利用:让技术成为助力
计算器:
熟练使用 “积分 / 导数计算”“统计分布函数” 功能,节省运算时间(如 A-Level 计算器可直接求正态分布概率,无需查表)。
画图软件:
用 GeoGebra 绘制函数图像,直观理解 “导数正负与函数单调性”“向量夹角与点乘结果” 的关系,抽象问题可视化。
避坑指南:这些 “雷区” 千万别踩
忽视教材,直奔真题:01
教材中的例题是考点最直接的体现,跳过教材会导致基础不牢,后期刷题效率低下。
只做难题,轻视基础:02
A-Level 数学 70% 都是中低档题,确保基础题正确率(90% 以上),再攻克难题,性价比更高。
步骤省略,依赖计算器:03
考试按步骤给分,即使结果错,写对公式和中间过程也能得一半分;计算器只是辅助,手动运算能力(如分式化简、解方程)不能丢。