2025年秋季爱德思大考考情回顾｜10月23日高数M2模块真题答案及考情分析

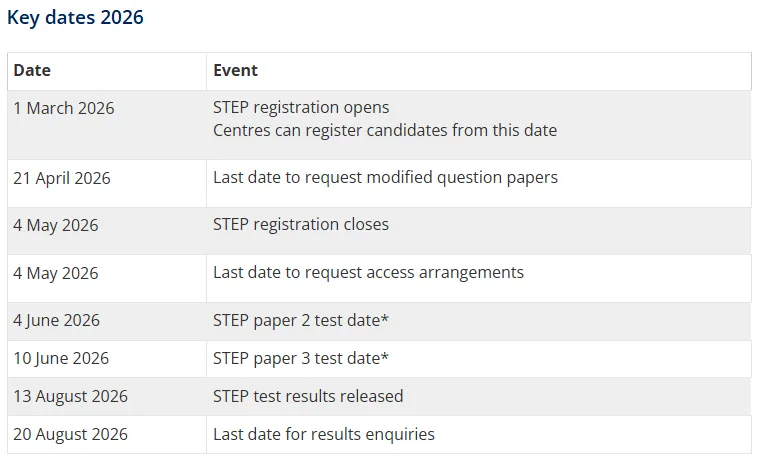
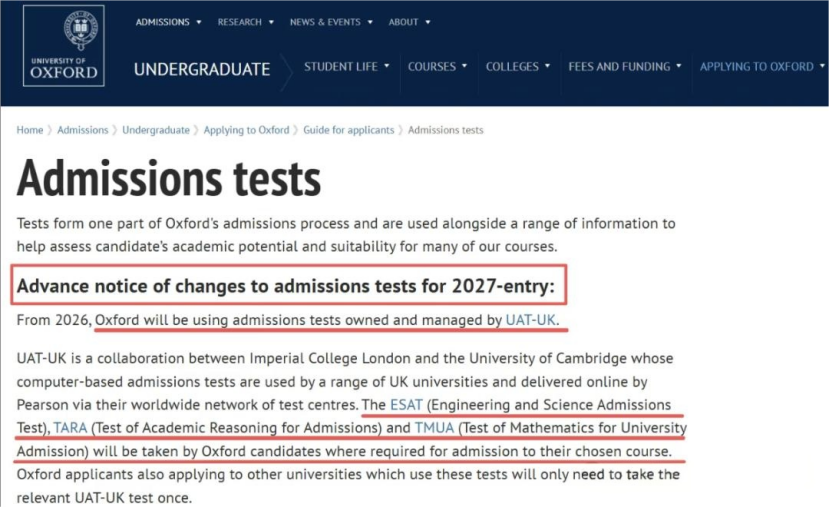
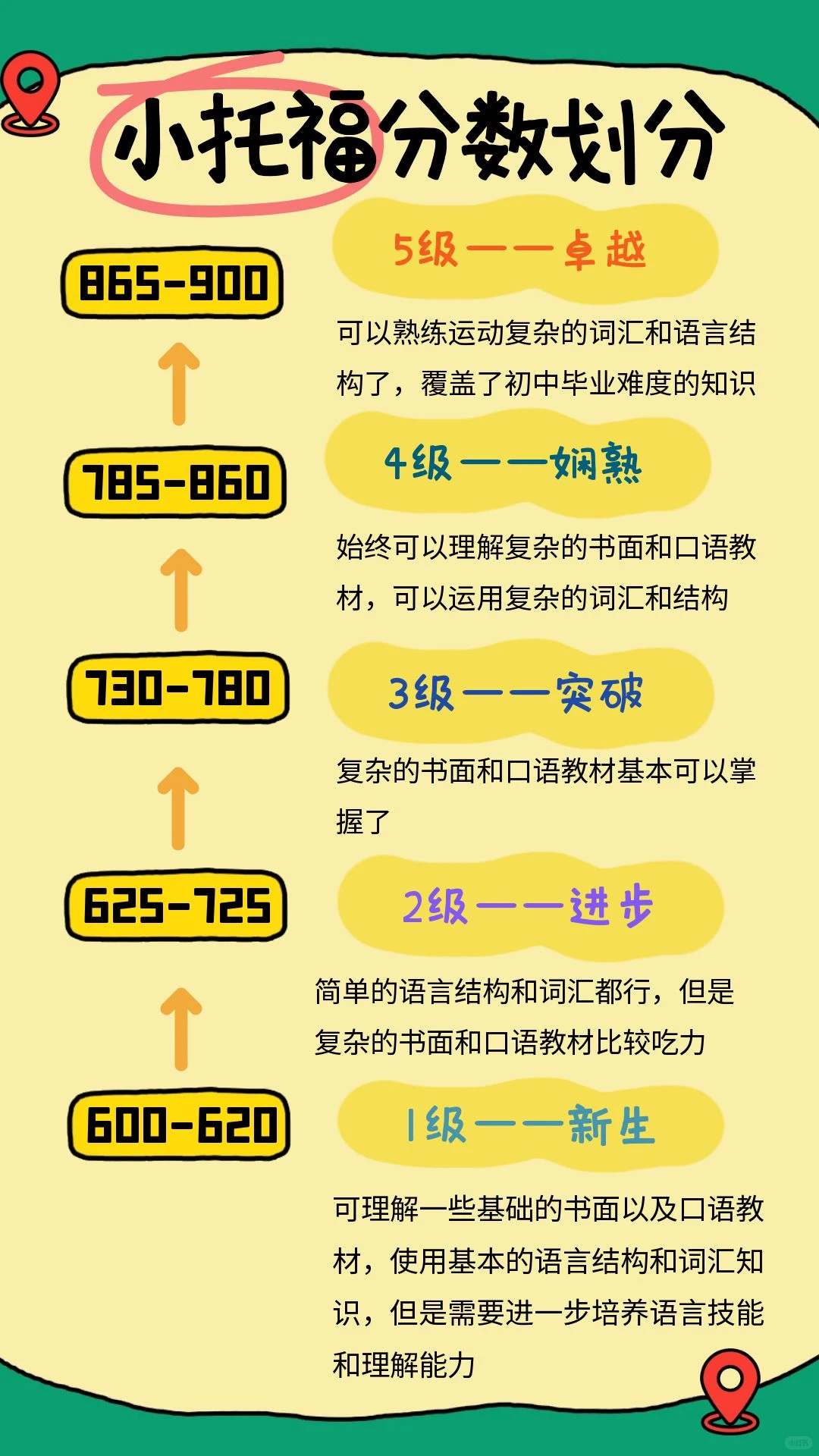
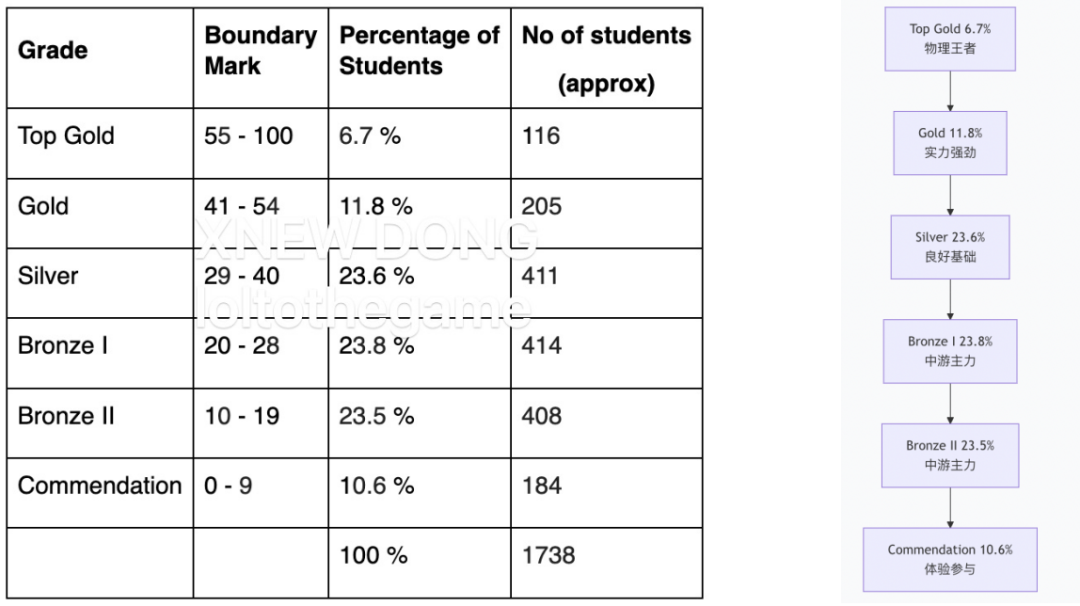
新鲜出炉！新通A+中心的胡老师和沈老师带来了M2详尽的答案、思路梳理及练习题对比，助力同学们为接下来的考试查缺补漏。

Alevel高数M2

试卷第⼀题

2017年6月M2第一题原题：

答案：

试卷第⼆题

2016年10月M2第一题原题

答案：

试卷第三题

2018年10月M2第三题原题

答案：

试卷第四题

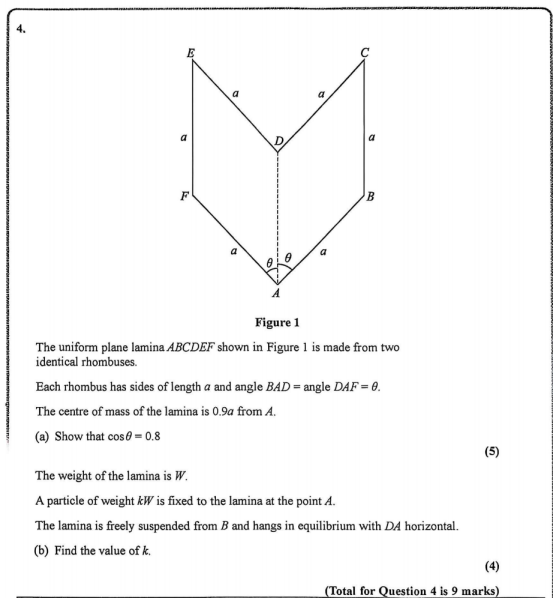
2015年1月M2第四题原题：

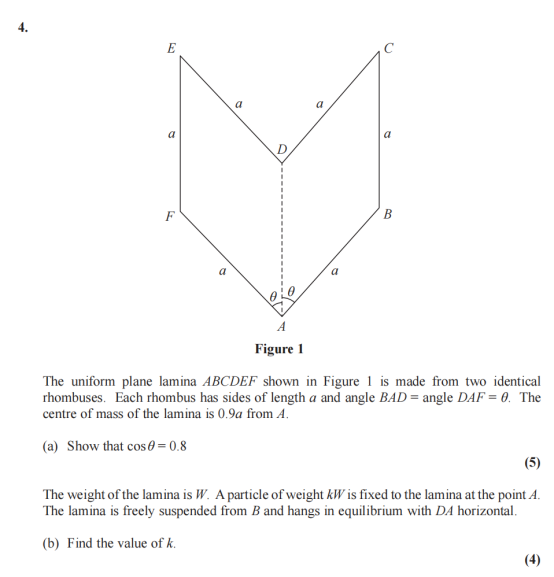
答案：

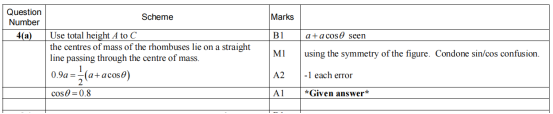
试卷第五题

2016年6月M2第五题原题：

答案：

试卷第六题:

2017年10月M2试卷原题：

答案：

试卷第七题:

2018年6月M2第6题原题：

答案：

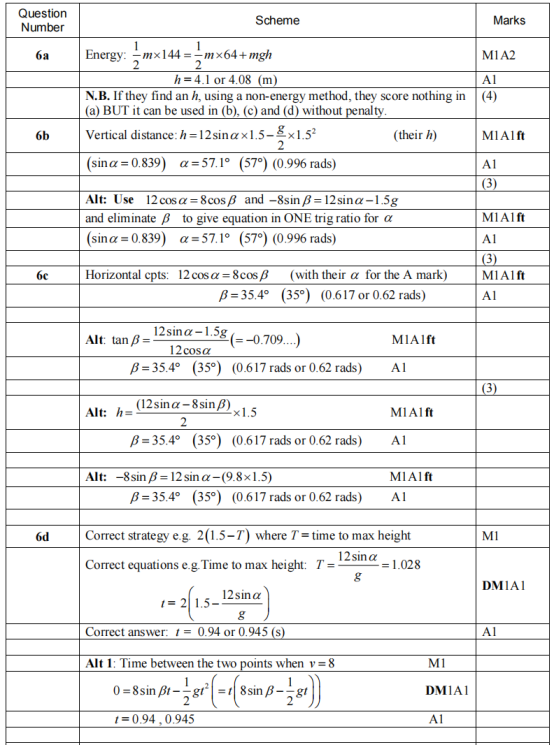
试卷第八题:

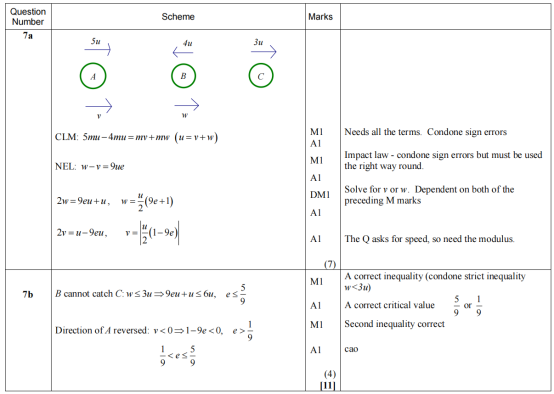
2014年1月M2第7题原题：

答案：

M2考试分析与总结

本次考试难度中等偏上，题目覆盖了力学M2的主要知识点，包括动量与冲量、质心计算、运动学、刚体平衡、变加速运动、斜抛运动以及碰撞问题。部分题目计算量较大，对学生的理解能力和代数运算能力要求较高，尤其是涉及复合几何形状的质心、多体碰撞和变加速运动的积分计算。

各题解题思路分析

第1题

考查冲量与动量的关系。已知质量和初速度，以及冲量向量，应用动量定理：

l=mv-mu

代入数据求出末速度向量，再计算其大小即为速度。解题关键在于向量运算。

第2题

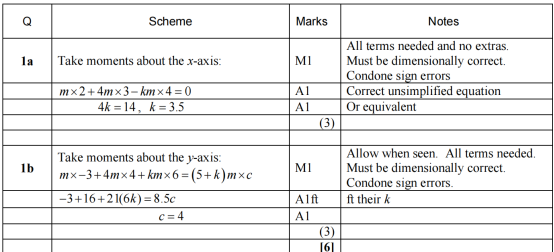
涉及质心坐标的计算。

· (a)利用质心y坐标为0的条件，列方程求解k。

· (b)将k代入x方向质心公式求出c。

题目较为直接，考查学生对质心公式的熟练应用。

第3题

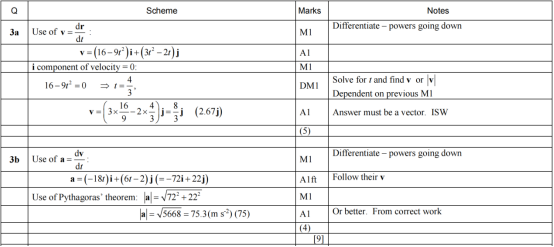
为运动学题，给出位置向量函数。

· (a)求速度向量，令其i分量为0（即平行于j）时解t，再代回求速度。

· (b)对速度求导得加速度，再代入t=4求模长。

注意题目要求不能用计算器，需手动完成微分与代数运算。

第4题

考查复合平面薄片质心。

· (a)将两个相同菱形组合，利用对称性和质心公式建立方程，解得cosθ=0.8。

· (b)在A点附加质点后悬挂于B，利用力矩平衡求k。

此题几何与力学结合，对空间想象和代数推导能力要求较高。

第5题

为刚体静力学问题，涉及受力分析与摩擦。

· (a)对B点取矩，求绳的张力。

· (b)利用力平衡（水平与竖直方向）求摩擦力与法向反力，进而求摩擦系数。

· (c)判断墙对杆的合力方向，需结合摩擦角概念。

题目综合性强，步骤较多，容易在力矩计算中出错。

第6题

考查变加速运动。

· (a)对加速度积分，利用初始条件求速度表达式。

· (b)令速度为零解t，求位移差即为AB距离。

积分运算和符号判断是关键，需注意速度为零的时刻对应位移的极值点。

第7题

为斜抛运动题，结合能量与运动分解。

· (a)利用机械能守恒求高度差。

· (b)(c)利用速度分解与时间关系联立求角度α和β。

· (d)分析速度小于8m/s的时间段，需解速度方程并判断区间。

题目综合性强，尤其是(d)问对运动过程的理解要求较高。

第8题

为多体碰撞问题，考查动量守恒与恢复系数。

· (a)对A、B碰撞列动量守恒与恢复系数方程，求碰撞后速度。

· (b)根据A反向运动且B、C不碰撞的条件，建立不等式求e的范围。

题目逻辑严密，需注意速度方向与不等式的建立。

总结建议

本次考试强调向量运算、积分应用、几何质心、力矩平衡和碰撞分析等核心能力。学生应加强代数推导与几何结合类题目的训练，如第4题。对于变加速运动（第6题）和多体系统（第8题），需熟练掌握积分与不等式分析技巧。

整体而言，考试要求扎实的基础与清晰的逻辑推理，建议平时练习时注重步骤完整与概念理解。