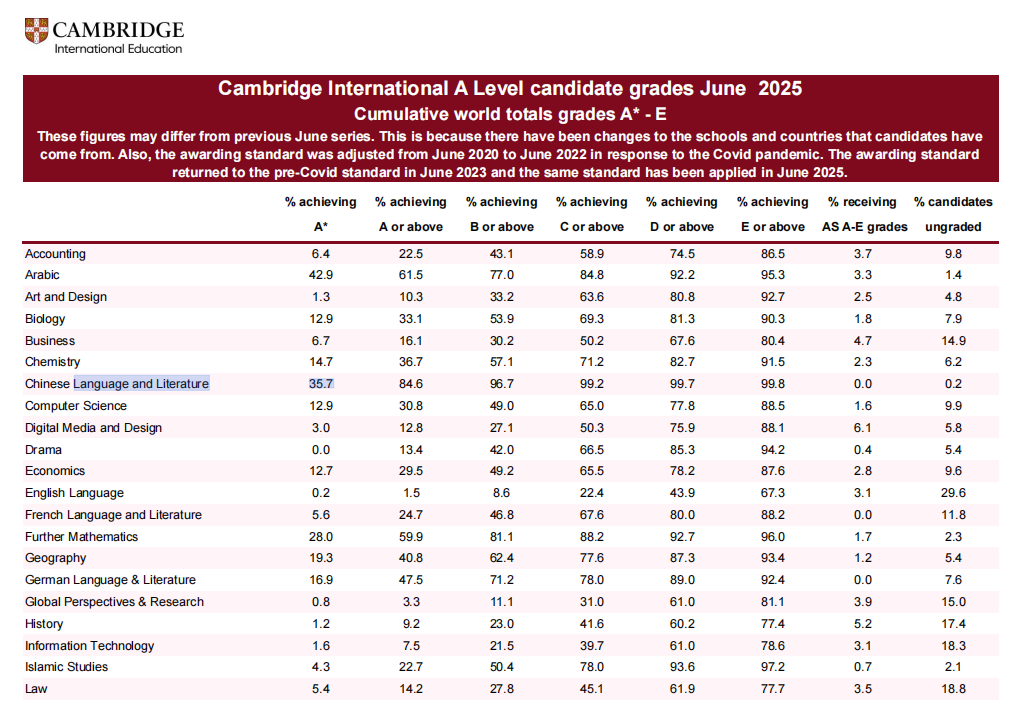
划重点!45%的5分率背后,这些考点每年必考,AP微积分BC作为大学先修课程中的“重头戏”,一直是许多优秀学子证明自己学术能力的首选。2024年全球AP微积分BC考试5分率高达约45%,这意味着只要准备充分,获得高分并非难事。
本文将为你揭秘2026年AP微积分BC考试的高频考点和命题方向,助你高效备考,轻松拿下5分!
✨ 核心高频考点梳理
1. 极限与连续性(Limits and Continuity)
极限计算(包括有理化、洛必达法则等)、连续性的定义与判断(三类间断点)、渐近线、以及最值定理、介值定理和零值定理的应用都是必考内容。
2. 导数(Derivative)及其应用
各种函数(显函数、隐函数、参数方程、极坐标函数)的求导,高阶导数都不容忽视。导数的应用更是重点:几何应用(切线与法线)、物理应用(运动学问题中的速度与加速度)、函数性质分析(单调性、极值、凹凸性、拐点)、微分中值定理等。
3. 积分(Integral)及其应用
不定积分(基本公式、换元法、分部积分法)和定积分(黎曼和、微积分基本定理FTC、反常积分)的计算需要熟练掌握。积分的应用包括积分中值定理、求面积(直角坐标与极坐标)、体积(旋转体体积、已知截面的体积)、弧长等。
4. 微分方程(Differential Equation)
可分离变量的微分方程、斜率场、欧拉方法是常见考点。
5. 无穷级数(Infinite Series)(BC特有)
这是BC考试的难点和重点,几乎每年简答题都有一整道大题。包括:数列与级数的收敛性判别(比较审敛法、比值审敛法、积分审敛法、交错级数审敛法)、幂级数的收敛半径与收敛区间、泰勒级数与麦克劳林级数的展开及应用(如函数逼近、误差估计)。
6. 参数方程、极坐标与向量函数(BC特有)
参数方程求导与求积、极坐标求面积与弧长、向量函数的微积分都需要重点掌握。
📊 各单元分值分布一览
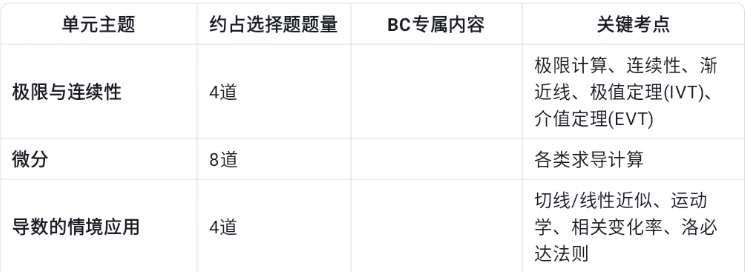
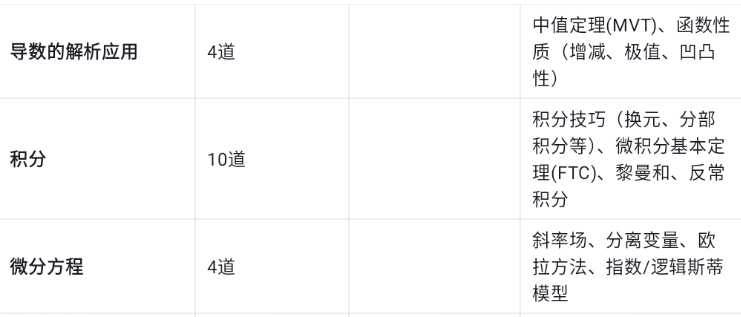

可用我们机构模考系统,还原真考,自动归纳错题,可以来联系我们获取高频词汇,也可以联系我们线下一对一辅导
🔍 六大高频题型预测
1. 极限与连续性的综合题:分析分段函数在分段点的连续性、可导性,或利用介值定理证明根的存在性
2. 运动学问题(参数方程或向量函数):给定粒子位置函数,求速度、加速度、速率、运动方向及总路程
3. 微分方程与斜率场:根据斜率场绘制特定解曲线,或求解可分离变量的微分方程并求特解
4. 积分应用求面积和体积:求曲线围成的面积(直角坐标或极坐标)、求旋转体体积(圆盘法、washer法)
5. 级数收敛性判断与泰勒级数:判断级数收敛性(收敛半径、收敛区间);将函数展开成泰勒级数或麦克劳林级数;利用泰勒多项式近似计算并估计误差
6. “有进有出”的综合应用题:描述一个情境(如水流入流出容器),给出两个变化率,要求利用积分计算净变化量、最大值、最小值等
📚 高效备考四大策略
1. 理解概念,非死记硬背
AP微积分考试越来越注重对概念的理解,仅仅背公式是不够的。要弄懂每一个定理和公式背后的含义。
2. 分类刷题,精炼错题
不要盲目采用“题海战术”。建议采取**模块化刷题**策略,每周集中精力攻克一个薄弱知识点。准备一个**错题本**,详细记录错题的原因、对应的知识点以及如何避免再次出错。
3. 熟练掌握计算器使用
考试中部分题目允许使用图形计算器。务必熟练掌握计算器进行函数绘图、求导、积分、解方程等操作,这能为你节省大量时间。
AP微积分BC虽然内容较多,但考点相对固定,规律性很强。只要掌握高频考点,针对性地进行练习,合理安排复习计划,取得5分并非难事。祝你2026年AP微积分BC考试顺利,一举拿下5分!欢迎随时来机构咨询