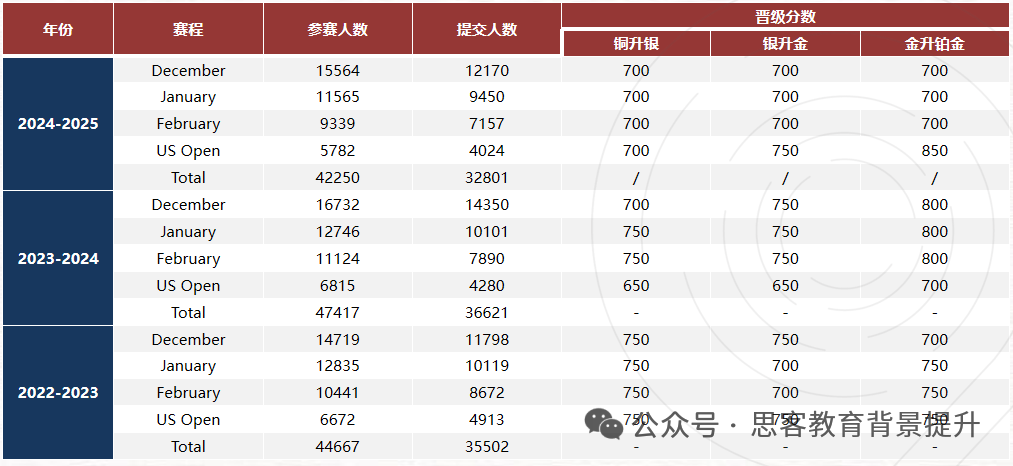
2026年AP微积分AB的高频考点和题型已经比较明确。最新的考纲没有重大调整,因此近年真题的考点分布有很强的参考价值。
考试结构与高频主题
为了让你对考试有整体把握,以下是考试的基本结构和各部分的高频主题:
第一部分:选择题 (45题,占总分50%)
主题:全面覆盖所有单元,尤其侧重对极限、导数计算(包括复合、隐函数) 以及积分基本概念的理解和应用。
第二部分:自由回答题 (6题,占总分50%)
主题:每道题通常聚焦一个核心应用领域。最常见的是积分与导数的综合应用题、积分的几何/物理应用、以图表为背景的微积分问题,以及运动学问题。
可用我们机构模考系统,还原真考,自动归纳错题,可以来联系我们获取高频词汇,也可以联系我们线下一对一辅导
简答题(FRQ)核心题型分析
简答题(6道题)是考试的重点和难点,其出题模式非常规律。根据2025年的真题回顾,可以总结出以下核心题型:
题型1:积分与导数综合应用题
典型考法:提供一个现实场景(如植物生长面积、阅读速度),给出相关函数。
核心考点:平均值的计算、中值定理的应用、利用导数分析变化率、最值问题。
备考提示:重点练习从文字描述中建立数学模型,并综合运用积分与导数工具解决问题的能力。
题型2:积分的几何应用
典型考法:给出平面图形边界曲线,求面积、体积(旋转体或已知截面的立体)。
核心考点:定积分求面积、圆盘法/垫圈法求体积、理解并设置正确的积分表达式。
备考提示:必须清晰画出草图,准确确定积分上下限和被积函数。
题型3:变限积分与函数分析
典型考法:给出函数 f 或其导数 f' 的图形,定义 g(x) = ∫f(t)dt,分析 g(x) 的性质。
核心考点:变限积分求导、利用 g'(x) = f(x) 和 g''(x) = f'(x) 分析原函数 g 的单调性、极值、拐点。
备考提示:这是连接微分与积分的经典题型,关键在于理解图形与函数性质之间的对应关系。
题型4:粒子运动学
典型考法:给出粒子位置、速度或加速度函数(或图像),分析运动状态。
核心考点:位置、速度、加速度的导数/积分关系、运动方向变化、速率增减的判断、净位移与总路程的计算。
备考提示:牢记 速度 与 速率 的区别,以及速度与加速度同号则速率增加这一关键结论。
题型5:微分方程(斜率场)与建模
典型考法:给出微分方程及其斜率场,或建立简单微分方程模型(如指数增长)。
核心考点:根据斜率场判断解曲线、使用分离变量法求解可分离变量的微分方程、理解解的含义。
备考提示:注意结合初始条件求特解,并练习解释解的现实意义。
题型6:隐函数求导与相关变化率
典型考法:给定一个隐函数方程,求导、求切线,或涉及多个相关变量的变化率问题。
核心考点:隐函数求导(尤其是涉及二阶导)、利用导数求切线方程、相关变化率。
备考提示:这是计算上的难点,务必注意对 y 求导时要乘以 dy/dx,并熟练解出所需表达式。
备考关键点
综合来看,为了高效备考,你需要特别注意以下几点:
突破计算核心:链式法则是基础中的基础,必须达到高度熟练,它贯穿于几乎所有复杂求导和积分换元中。
强化核心应用:运动学(位置-速度-加速度)和几何应用(面积与体积)是每年简答题的“常客”,需重点练习。
规范解题步骤:在简答题中,清晰地展示你的推理和计算过程,甚至用文字解释步骤,与得出正确答案同样重要,这是评分的关键。
备考AP微积分AB,核心在于理解而非记忆。一位高分考生总结道:“做真题时我发现自己总在相同类型的题目上出错,但当我理解了背后的概念而不是单纯记忆解题步骤,这些问题就迎刃而解了。”