AMC8数学竞赛与小升初分班考都备受家长和学生的关注。AMC8作为一项国际知名的数学竞赛,旨在培养学生的数学思维和解题能力,而分班考则是学校用于对学生进行分层教学的重要依据。
两者虽然在目的和形式上有所不同,但在数学学习的路径上却有着诸多交集,它们都对学生的基础知识、逻辑思维和解题技巧提出了较高要求。
1.重点加强数学基本能力
数学运算能力、逻辑推理能力、质疑创新能力
2.锻炼数学思维和解决问题能力
初中数学更注重逻辑思维和解题方法,可以让孩子预习初一上册的知识点,尝试做课本简单的例题,了解基本的概念。并且要引导孩子去反问和思考
01、AMC8竞赛与分班考的区别和联系
◆AMC8的核心内容
AMC8(美国数学竞赛8)是一项面向8年级及以下学生的国际数学竞赛,其内容涵盖了小学至初中阶段的数学知识,主要分为四大模块:
-基础代数:包括整数、分数、小数、比例、方程等,占比约35%-45%。
-基础几何:涉及平面图形的性质(如三角形、四边形、圆)以及立体几何图形,占比约20%-30%。
-基础数论:如质数、整除性、最大公约数与最小公倍数等,占比约15%。
-基础组合:包括排列组合、概率计算等,占比约15%-20%。
◆分班考的特点
分班考是学校为了对学生进行合理分层教学而组织的考试,其内容和形式因学校而异。
通常,分班考会涵盖以下内容:
- 语文、数学、英语:这是大多数学校的必考科目。
- 拓展内容:部分学校还会考查生活常识、奥数、科学、时事新闻等。
- 难度与深度:对于有理科特长或竞赛性质的班级,考试难度会高于常规教学大纲。
◆AMC8与分班考的联系
1. 知识基础:AMC8的许多考点与小学和初中数学课程重叠,如基础代数、几何和数论。这些知识也是分班考的重要内容。
2. 能力提升:AMC8注重培养学生的逻辑思维和问题解决能力,这些能力在分班考中同样重要。
3. 竞争优势:AMC8成绩优异的学生在分班考中往往更具优势,因为他们在数学思维和解题技巧上已经得到了锻炼。
◆AMC8与分班考的区别
1. 考试目的:
AMC8:旨在激发学生对数学的兴趣,培养逻辑思维能力,并为更高阶的数学竞赛做准备。
分班考:主要是为了对学生进行分层教学,根据学生的能力和水平分配到不同的班级。
2. 考试内容:
AMC8:内容较为广泛,涵盖小学和部分初中数学知识,注重知识点的综合运用。
分班考:内容可能因学校而异,除了数学,还可能包括语文、英语和其他拓展内容。
3. 难度与深度:
AMC8:难度较高,尤其是后10题,需要学生具备较强的数学素养和解题能力。
分班考:难度因学校而异,但总体上可能更侧重于对常规教学内容的掌握。
AMC8与分班考虽有联系,但也有明显区别。AMC8更注重数学思维和解题能力的培养,而分班考则更侧重于对学生综合能力的评估。
对于准备参加分班考的学生来说,备考AMC8不仅可以提升数学能力,还能为分班考提供有力支持。
AMC8竞赛水平测试
AMC8竞赛规划+课程咨询
02、AMC8怎么备考
5-6月:梳理AMC8竞赛基础知识
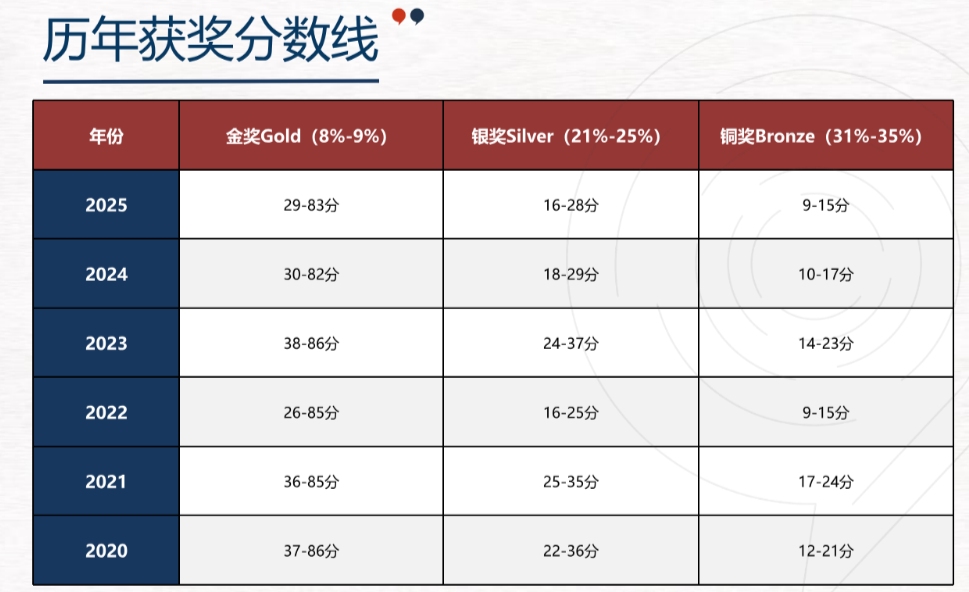
对于0基础备考AMC8竞赛的小朋友和家长,首先要做的一点是了解AMC8竞赛的基础知识,包括AMC8竞赛的考试内容/考试时间/奖项设置/考试难度/获奖难度等
如果各位家长对以上的内容已经有了初步的了解就可以开始梳理AMC8竞赛的基础知识梳理,针对考纲,梳理出AMC8竞赛的考点。包含小学全部数学基础知识、初中七八年级核心数学知识以及小学奥数部分知识点,考试范围比较广泛,理知识点相对来说也比较多。
7-9月:分模块针对性复习
模块化复习各个知识点。AMC8竟赛考察代数、几何、数论、组合四大模块的知识点,在整体梳理完知识点后,就可以进行分模块化的复习,更有针对性,也能更清楚的了解孩子的薄弱项是什么。
数论:重点攻克整除性、质数、余数问题,例如运用模运算快速解决周期问题。
组合计数:掌握排列组合、容斥原理,可借助树状图或公式化复杂的计算情况。
几何进阶:深入学习相似三角形、圆与扇形、立体几何展开图,比如采用切割法求解体积问题。
逻辑推理:学会应对最值问题、操作类题目,运用逆向思维或极端情况分析来解题
机构老师总结的【AMC8考前100问】涵善AMC8竞赛高频考点和重要考点,帮助学生查漏补缺。还有为考生冲击AMC8好成绩提供建议和复习思路。
10-11月:刷题训练,查漏补缺
分类训练完后,通过真题来检验复习成果,同时,真题也能更清楚的让孩子了解自己还有哪些知识点是不备考不足的,至少完成近10年的真题。在刷题的过程中也要总结AMC8竞赛的高频考点以及错题本,方便后期冲刺复习使用。
12-1月:模拟考试,分配考试时间
1月份考试,最后一段时间就需要定时模拟考试,严格按照考试的流程进行模拟考试,熟悉考试流程,也要在这个模拟的过程中分配各个题目的考试时间。
时间分配:
1-10题控制在8分钟内完成,11-20题花费15分钟,21-25题用12分钟,预留5分钟进行检查。
取舍原则:
遇到2分钟内没有解题思路的题目,先暂时跳过,优先保证单题的正确率。