AMC12数学竞赛备考攻略

首考AMC12数学竞赛的宝子看这里！今天给大家扒一扒 AMC12数学竞赛备考的常考内容和题目设置，纯干货预警，收藏起来慢慢看！

1、AMC12数学竞赛备考学习内容

AMC12数学竞赛面向 12 年级及以下学生，考察代数、几何、数论、组合四大模块，难度比 AMC10数学竞赛更上一层楼，还会涉及三角函数、复数、多项式定理等高中进阶知识。具体来看：

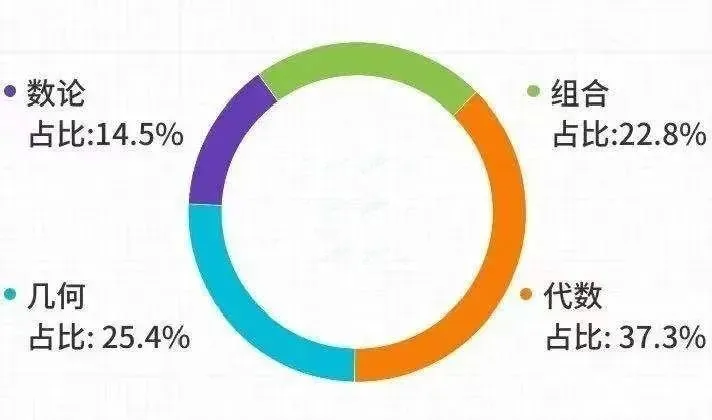
✅代数部分

高频考点：二次函数最值、分式方程、递推数列、对数运算

难点突破：多项式因式分解（如有理根定理）、不等式证明（Cauchy-Schwarz 技巧）

✅几何部分

核心内容：圆与相似三角形（托勒密定理、弦切角定理）、三维几何体积计算

解题关键：辅助线构造技巧、坐标系建模（解析几何思维）

✅数论部分

必学知识点：同余方程（中国剩余定理）、质因数分解（唯一分解定理应用）

进阶题型：欧拉函数与费马小定理的综合运用

✅组合数学

基础题型：排列组合计数（容斥原理）、概率期望计算

高阶技巧：递推法解组合问题（如斐波那契模型）、生成函数初步

2、AMC12数学竞赛备考必备公式

AMC12数学竞赛备考务必熟练掌握这些公式，让几何计算快如闪电、代数推导精准无误，数论同余灵活切换，组合建模信手拈来 —— 公式熟练度直接决定你的答题速度与正确率！

一、几何板块

海伦公式S=s(s−a)(s−b)(s−c)得出三角形面积S。

维维亚尼定理：它表明在等边三角形中，三角形内任意一点到三边的距离之和等于该等边三角形的高。

托勒密定理:AC⋅BD=AB⋅CD+AD⋅BC。

圆幂定理（切线、割线、相交弦）

二、代数板块

对数换底公式:logab=logcalogcb（a>0且a=1；c>0且c=1）。

欧拉公式:eiθ=cosθ+isinθ

棣莫弗定理:若z=r(cosθ+isinθ)，那么zn=rn(cosnθ+isinnθ) 。

柯西-施瓦茨不等式

三、计数板块

二项分布：若随机变量X服从参数为n（试验次数）和p（每次试验成功的概率）的二项分布，记为X∼B(n,p) ，则P(X=k)=Cnkpk(1−p)n−k ，其中Cnk=k!(n−k)!n!

对称性原理：在某些计数问题中，当问题所涉及的对象或情况具有对称性时，可以利用对称性简化计数过程。

路线问题：若要从点(0,0)走到点(m,n) ，只能向右或向上走，那么最短路径的条数为Cm+nm=Cm+nn 。

解析几何在概览问题中的应用

四、数论板块

质因式分解、贝祖定理、丢番图方程、欧拉函数的应用

3、AMC12数学竞赛备考历年真题

4、机构AMC12数学竞赛培训班课程

📐AMC12数学竞赛培训基础段-50小时

串联AMC12数学竞赛知识点进行梳理，夯实AMC数学竞赛考点基础！

📐AMC12数学竞赛培训强化段-30小时

结合考点进行专题分类讲解，解题方法训练

📐AMC12数学竞赛培训冲刺段-30小时

真题模考点评，对考点进行查漏补缺，多次模考，掌握答题技巧。

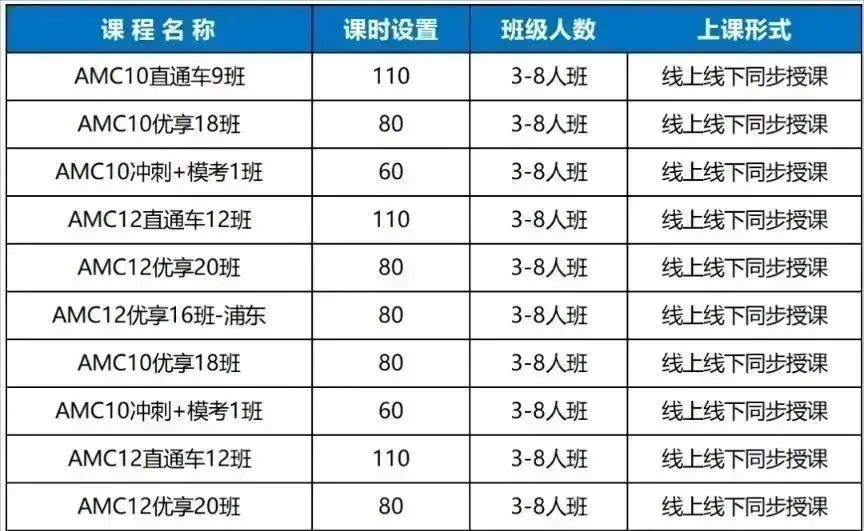
▶课程目的：针对重难点科目进行预习和同步学习，补缺补差，难度层层递进，帮助学生举一反三。

▶课程内容：精选主要考核知识模块，配套高频考点强化练习，易错题汇总分析，解决练习不足，缺少技巧性答题的问题。

▶教学方式：精研教材与历年真题库，精准捕捉学生弱项，击破重点难点。

▶课程类型：3-6人小班授课/一对一授课模式

▶授课模式：在线面授均可

▶授课语言：中英双语教学/纯英文授课