一线城市孩子都在学的AMC8数学竞赛培训课程都在学什么？附AMC8课程大纲

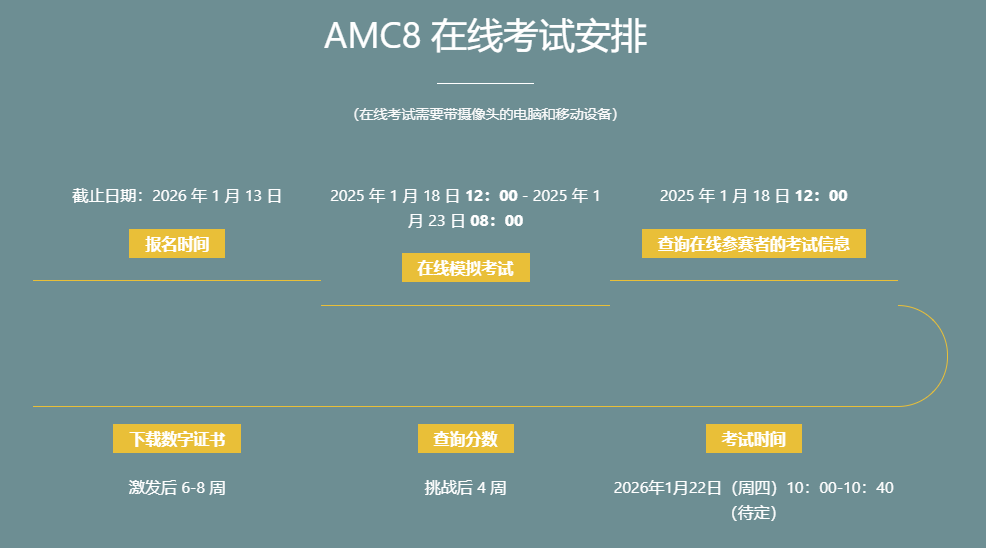
在当今竞争激烈的教育环境下，越来越多的家长开始关注各类学科竞赛，希望为孩子的学业发展增添助力。其中，AMC8数学竞赛在一线城市的家长圈中热度持续攀升，成为众多孩子提升数学能力、冲击奖项的热门选择。

今天，我们就来深入探讨一下一线城市孩子都在学的AMC8数学竞赛培训课程的奥秘，看看它究竟能为孩子们带来什么帮助👇

PART.01AMC8数学竞赛培训课程的作用普娃实现逆袭提升

AMC8数学竞赛培训课程是一个系统提升数学能力的绝佳机会，通过专业指导，孩子们能够深入学习📚数学知识，填补知识漏洞，完善知识体系。

不仅可以掌握不同类型题目的解题方法和技巧，还能够培养良好的数学思维习惯。从历年数据来看，许多孩子通过认真参与AMC8培训课程，在竞赛中取得了显著进步，不仅提升了自信心，还为后续的数学学习打下了坚实的基础。

牛娃冲击更高奖项

牛娃们本身已经具备了扎实的数学基础和较强的学习能力，AMC8数学竞赛培训课程对他们而言，是冲击更高奖项、挑战自我🏆的平台。

我们的课程中会涉及到一些高难度的拓展内容和竞赛策略讲解，能够满足孩子们对知识深度和广度的追求。通过与同样优秀的同学交流切磋，能够发现自己的优势与不足，进一步提升自己的解题速度和准确率。

在历年的AMC8竞赛中，不少经过专业培训的牛娃成功斩获全球前1%的优异成绩，为自己的升学简历增添了浓墨重彩的一笔，为未来申请顶尖学校积累了强大的竞争优势。

PART.02AMC8数学竞赛培训课程内容揭秘

01基础代数

数的认识与运算：深入学习整数、有理数、无理数、实数的概念及运算，熟练掌握数轴和直角坐标系的运用，为后续的代数学习奠定基础。

方程与不等式：学习多元一次方程、简单二次方程和简单不等式的解法，培养学生运用方程和不等式解决实际问题的能力。

数列基础：认识简单数列，掌握通项公式和求和方法。通过有趣的数列游戏，理解数列的规律和特点，提高孩子们对数列的敏感度。

代数技巧提升：教授基本的代数技巧，如因式分解、代数式化简等，提升代数运算能力和解题灵活性。

02基础几何

几何作图基础：掌握基础几何作图方法，培养动手能力和空间想象能力，加深对几何图形的直观认识。

平面几何图形：深入研究平面欧氏几何中的点、线、三角形、特殊四边形、圆等图形的性质和判定方法。通过对各种图形的观察、分析和证明，理解图形之间的内在联系，提高逻辑推理能力。

图形周长与面积计算：熟练掌握规则图形的周长和面积计算公式，并能运用这些公式解决实际问题。同时，学习求解不规则图形周长和面积的方法，如割补法、平移法等。

立体几何初步：认识规则立体几何图形，了解它们的表面积和体积计算公式。通过实物模型展示和多媒体演示，帮助学生建立立体几何的空间概念。

03基础数论

奇偶分析：学会运用奇偶性分析解决数学问题，如判断整数的奇偶性、分析运算结果的奇偶性等。通过一些有趣的数学谜题，让学生体会奇偶分析在解决实际问题中的应用。

整除性质：深入研究整除的性质，掌握能被2、3、4、5、9等数整除的数的特征，学会求最大公约数和最小公倍数，通过实际例子理解整除性质的实际应用。

同余问题：初步了解同余的概念和性质，学会解决简单的同余问题。

04基础组合

韦恩图：学会使用韦恩图来表示集合之间的关系，解决集合运算和计数问题。

排列组合与概率入门：了解排列、组合的基本概念和计算方法，初步学习概率的计算。

阶乘与二项式系数、杨辉三角形：认识阶乘和二项式系数的概念，了解杨辉三角形的规律和应用。通过简单的数学推导和实例练习，让学生掌握阶乘和二项式系数的计算方法，以及杨辉三角形与二项式展开的关系。

PART.03AMC8课程大纲详细解读

帮助学生全面掌握AMC8竞赛所涉及的数学知识和技能，提升学生的数学素养。培养学生的数学思维能力，包括逻辑思维、创新思维、批判性思维等，提高学生解决问题的能力。

课程特色

专业师资团队：授课教师均具有丰富的AMC8竞赛教学经验，熟悉竞赛的命题规律和解题技巧，能够为学生提供专业、高效的指导。

个性化教学：根据学生的基础和学习进度，制定个性化的学习计划和辅导方案，满足不同学生的学习需求，确保每个学生都能在课程中有所收获。

丰富的学习资源：提供丰富的学习资料，包括教材、练习题、历年真题、模拟试卷等，让学生有充足的练习机会，巩固所学知识。

线上线下结合：采用线上线下相结合的教学模式，学生可以根据自己的实际情况选择适合自己的学习方式，灵活安排学习时间。

机构国际总部位于上海，目前在北京、深圳、广州、杭州、苏州、合肥、成都、南京、武汉、无锡、宁波、青岛、重庆、天津、香港、常州、厦门、新加坡等城市也均开设30+线下校区，在线面授均可！