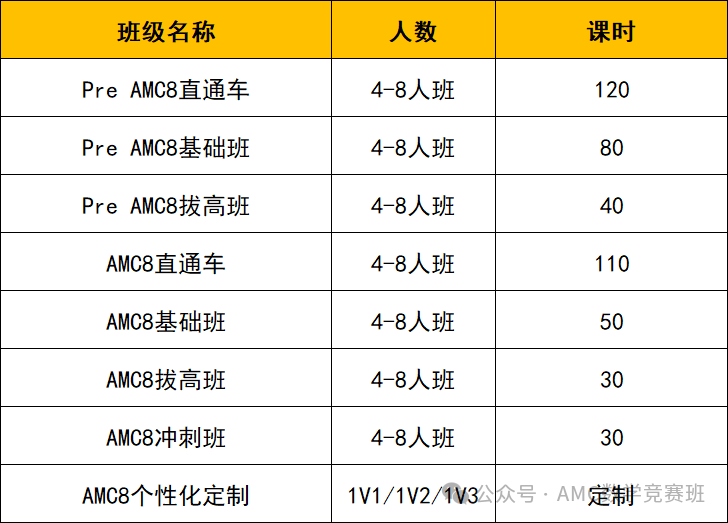
对于目标冲击美本Top30、国际高中或后续进阶AIME竞赛的学生来说,AMC10是绕不开的关键跳板。但很多家长和学生对amc10竞赛难度解读、考试内容、备考攻略仍有疑问——今天这篇文章,就从核心信息到实用攻略,帮你彻底读懂AMC10,避免备考走弯路!
01AMC10数学竞赛规则解读
AMC10由美国数学协会(MAA)面向全球中学生举办,是晋级AIME、USAMO乃至IMO的“第一扇门”,也被中国学生视为冲击国际赛事的重要起点。
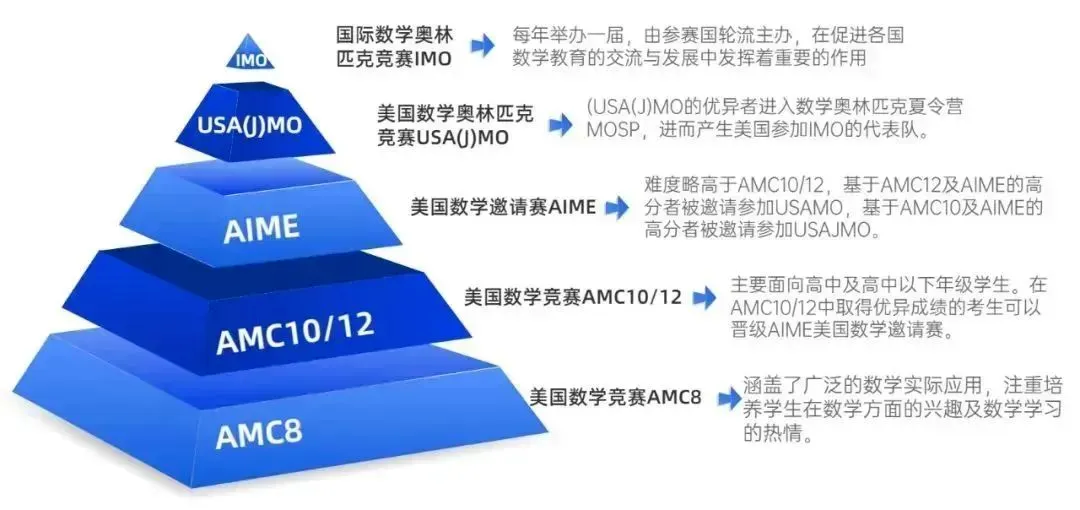
✅ 竞赛语言:试卷同步提供中文与英文版本
✅ 参赛形式:线下考试,共25道单项选择题
✅ 参赛年级:仅限10年级及以下,且参赛当天年龄≤17.5岁
✅ 比赛日期:
A卷 2025年11月6日
B卷 2025年11月14日
✅ 比赛内容:初三至高一数学知识,包括代数基础、几何基础(如勾股定理、面积与体积计算等)、简单数论与概率,不涉及三角函数、高等代数及高等几何内容。
✅ 评分标准:每题答对得6分,未作答得1.5分,答错不扣分,满分150分。
✅ 两卷说明:A、B卷独立命题,难度与范围相近,可单独或同时参加,取高分用于评奖及AIME晋级。
AMC10竞赛含金量
🔸AMC10数学竞赛在全球享有高度认可,北美地区对其重视程度尤为突出。表现优异的参赛者可晋级至AIME,进而获得参与国际数学奥林匹克竞赛选拔的资格。
🔸竞赛题目覆盖代数、几何、数论及组合数学等核心数学领域,难度梯度合理且兼具挑战性,能够高效考察学生的数学思维逻辑与实际解题能力。
🔸参与AMC10并斩获高分,能显著优化个人学术履历,在申请顶尖高中或高校时具备明显优势,尤其在STEM相关专业的申请中,这种优势更为突出。
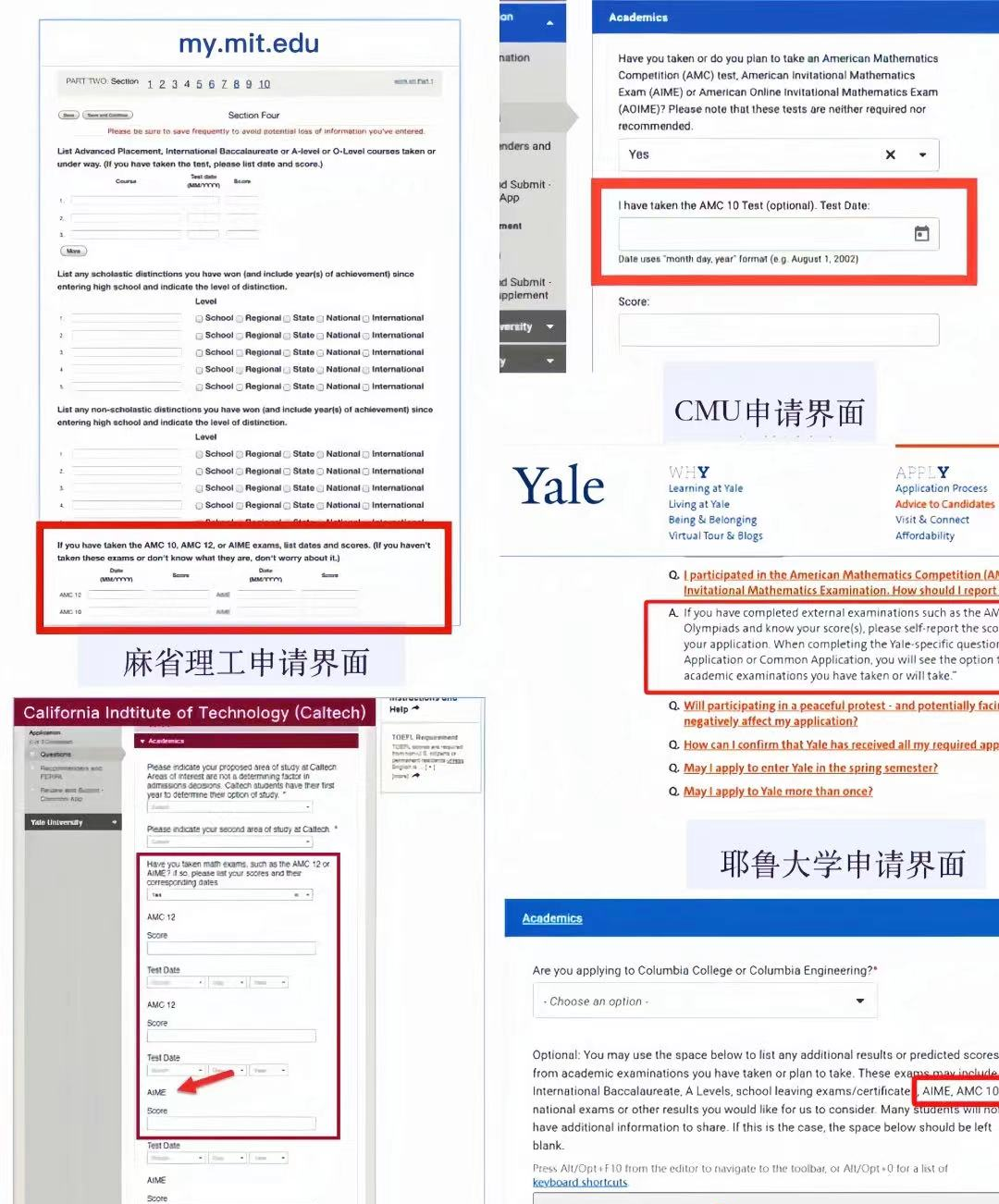
🔸AMC10竞赛成绩有效期长久,是评估学生数学能力的关键指标。众多院校与教育机构常将其作为奖学金评定、特殊人才培养项目选拔的核心参考依据。
🔸系统备考AMC10的过程,可帮助学生夯实数学基础,同时锻炼逻辑推理与问题解决能力,为后续的学术学习及各类数学竞赛参与奠定扎实基础,带来长期助力。
02AMC10竞赛难度解读
🌈前10题(基础题)
侧重考查基础运算能力与核心数学概念,例如基础代数运算、几何基本性质等。不过,部分题目会暗藏细微陷阱,学生若审题或计算时疏忽,很容易出现错误。
🌈11-20题(中等难度题)
要求对知识点进行灵活运用,涵盖复杂数论问题、组合计数问题、几何构造题等类型,解题过程需运用特定技巧,无法仅靠基础公式直接解答。
🌈21-25题(高难度题)
难度接近AMC12竞赛或AIME邀请赛水准,往往需要运用创造性思维——比如通过构造特殊案例、采用逆向推理等方式突破。普通学生面对这类题目时,往往会陷入毫无解题思路的困境。
AMC10考察内容
代数
代数是AMC10核心考察模块,占比达30%-40%,题目主要涵盖方程与不等式、函数、数列、多项式四大类内容。
- 方程与不等式:包含线性、二次、绝对值、分式等类型的方程解法,以及各类不等式的求解思路。
- 函数:核心考查一次、二次、指数及对数函数的基础性质,同时涉及函数图像的分析与应用。
- 数列:等差数列、等比数列的通项公式与求和公式是高频考点,偶尔会纳入递推数列的相关题目。
- 多项式:因式分解、多项式除法、韦达定理等知识点的出现频率较高,是代数部分的重要得分点。
几何
几何部分在试卷中的占比为20%-30%,涉及平面几何与立体几何两大板块,其中平面几何是考查重点。
- 平面几何:三角形、四边形、圆形的性质是考查核心,涵盖相似、全等判定,以及勾股定理、正弦定理、余弦定理的应用。
- 面积与体积:需计算多边形、圆形的面积,以及长方体、圆柱、圆锥等简单立体图形的体积。
- 坐标系几何:重点考查直线、圆、抛物线在坐标系中的方程特征与几何性质,偶尔会考查距离公式与斜率相关问题
数论
数论题目占比通常在10%-20%之间,整体难度偏高,解题需掌握特定技巧,是区分学生水平的关键模块。
- 整除与质数:涉及最大公约数、最小公倍数的计算,以及质因数分解的应用,是数论部分的基础考点。
- 模运算:以同余概念为核心,费马小定理等基础数论知识在考题中偶尔涉及,需理解并灵活运用。
- 数字性质:奇偶性判断、完全平方数特征、数字位数分析等是高频考查方向,题目常需结合逻辑推理求解
组合
组合数学在AMC10中的占比通常为15%-25%,题目形式灵活多变,对逻辑思维能力要求较高。
- 排列组合:涵盖基础排列组合公式,以及容斥原理、鸽巢原理的实际应用,需结合题目场景选择合适方法。
- 概率:主要考查古典概型、条件概率的计算,以及期望值的求解,需掌握基本概率模型。
- 计数问题:包括路径计数、图形计数等类型,解题需具备较强的逻辑分析能力,常需拆解问题逐步推导。