AMC 美国数学竞赛作为全球顶流中学生数学赛事,近年参赛人数激增,竞争越来越激烈!不少 AP、Alevel、IB 体系的学生都犯愁:自家体系的数学知识怎么衔接 AMC数学竞赛?怎么备考AMC才能高效不费力?
别再盲目刷题浪费时间!今天就针对不同课程体系的特点,拆解专属 AMC 备考思路,帮你找准AMC知识衔接点、避开备考误区,用对方法少走弯路。
AMC数学竞赛考什么?
美国数学竞赛(AMC)是由美国数学协会(MAA)主办的全球性数学竞赛,覆盖从初中到高中的多个级别,不同级别的考试内容有所不同:
✍AMC8:
①代数(40%):代数运算、代数应用题、数列、平面直角坐标系与一次函数、方程
②几何(12-20%):角度问题、勾股定理、圆与扇形、立体图形的表面积和体积、相似三角形、多边形的周长与面积
③数论(16-24%):整除、数位的周期循环、因数倍数、最大公因数与最小公倍数、质数与合数、余数
④组合(8-16%):概率、逻辑推理、统计、排列组合、容斥原理
✍AMC10:
①代数(38%):代数运算、多项式公式、多项式运用、多项式根、等比数列、等差数列、特殊数列、均值、中位数和众数、方程组、行程问题
②几何(29%):角、三角形长度和面积、特殊三角形、相似三角形、四边形、复杂形状的长度和面积、圆、解析几何、多边形、立体几何
③数论(19%):质数和因数、整除性、最大公约数和最小公倍数、余数定理、代数数论综合、进制、方程、杂项数论
④组合(14%):概率、排列组合、分类讨论、互补计数、容斥原理、插板法和隔板法、期望值、组合恒等式、概率、几何计数、几何概率、递归
✍AMC12:
涵盖AMC10所有内容,新增以下高阶内容:
①代数进阶:复数运算、三角恒等式、数学归纳法
②数论深化:费马小定理、二次剩余、高次同余方程、丢番图方程
③几何拓展:三维向量、射影定理、托勒密定理、圆锥曲线初步
④组合创新:图论基础、随机过程与期望、生成函数
不同体系怎么备考?
AP体系学生
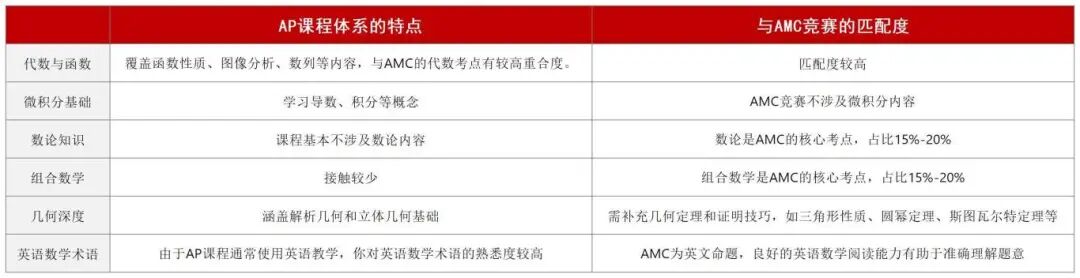
可以看到AP课程在数论和组合这两个模块接触较少,因此需要系统学习:
✅攻克数论与组合:
◎ 数论:从基础的整除性质、质数与合数、最大公约数与最小公倍数开始,逐步深入到模运算、同余方程和费马小定理。这些知识对AP的学生来说是全新的,需要投入更多时间。
◎ 组合数学:重点理解计数原理、容斥原理以及概率的基本概念和应用。多做计数问题,训练思维的严谨性。
✅提升几何思维:
AP课程中的几何知识多依赖于解析方法,但AMC更强调平面几何的定理和巧妙的辅助线,需要补充学习三角形、圆的性质、四点共圆等知识,并多做一些纯几何的证明题。
ALevel体系学生
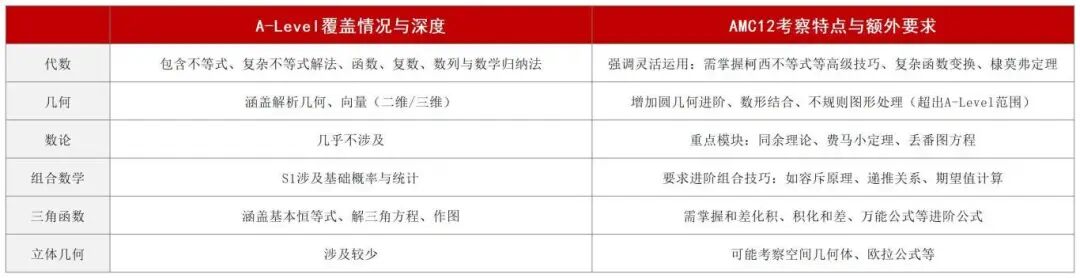
A-Level数学与AMC竞赛,特别是AMC12,有大约50%的内容是重合的,但也包含一些A-Level课程中未涉及或深度不够的内容,因此需要:
✅数论:需要完成从零到精通的突破,这是A-Level学生最大的盲区,但却是AMC的必考核心。从整除性、质数与合数、最大公约数、最小公倍数开始,这些概念相对直观。
✅进阶组合数学:A-Level S1的组合基础非常浅,AMC要求高得多,需要学习容斥原理、递推关系等高级计数技巧。
✅几何:A-Level过度依赖解析几何和向量,缺乏综合几何的证明和推导能力。要熟练记忆并证明圆幂定理、塞瓦定理、梅涅劳斯定理、托勒密定理,以及补充三角恒等式的和差化积、积化和差的公式、
IB体系学生
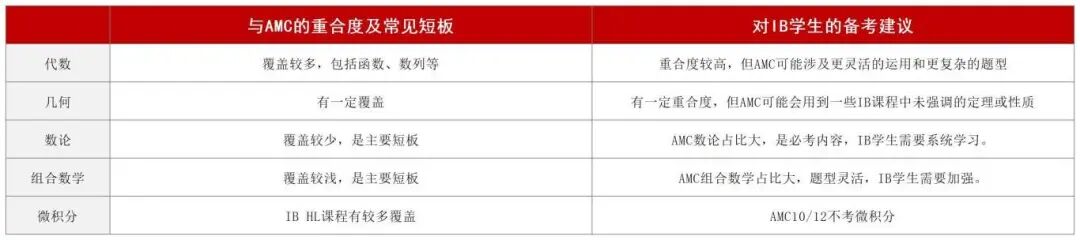
IB数学对数论、组合数学的覆盖极少,而这两类题型占 AMC10/12 的 40%-50%,是晋级 AIME 的核心,需针对性弥补:
✅数论:整除性与质因数分解;同余定理;最大公约数与最小公倍数;
◎ AMC12 进阶:费马小定理、二次剩余。
✅几何:排列组合进阶;容斥原理;递推计数;
◎ AMC12 进阶:生成函数、概率期望。
✅解题技巧:IB 数学强调 “完整步骤推导”,但 AMC 是 75 分钟 25 题的选择题,速度与技巧优先。需要提高解题速度,快速破题。
为什么要参加AMC数学竞赛?
01升学核心加分项
●对于计划留学的学生:美国藤校、英国 G5)、加拿大 UBC 等院校,在本科申请中会明确关注 AMC 成绩,尤其是 AMC12 前 5%或晋级 AIME、甚至前 1%的成绩,能直接证明学生具备应对大学理工科学习的数学思维与逻辑能力。
●对于国内升学的学生:AMC 经历可丰富综合素质评价档案,清北复交等高校的理工科强基项目,会优先关注有 AMC/AIME 经历的学生,认为其具备更强的抽象思维与问题解决能力。
02提高数学学术能力
AMC 的核心价值在于培养抽象思维、逻辑推理、创新解法,可以让学生完成从 “被动接受知识” 到 “主动解决问题” 的关键转变。AMC 的考点,如数论、组合数学是学校课程中较少涉及,但却是理工科学习至关重要的内容。
03接触多元数学文化
AMC 的命题团队来自全球各地,题目设计融合了不同国家的数学思维。备考过程中,学生可接触到国际通用的解题方法,以及不同语言环境下的数学表达,可以为未来阅读英文数学教材打基础。
机构AMC数学竞赛辅导
在AMC 的高学术门槛下,从复杂题型的快速破题,到思维盲区的精准突破,每一步都考验着知识储备与思维深度,不少同学常因找不到适配的进阶路径而陷入瓶颈。
机构推出了AMC8/10/12培训课程,为不同阶段的你量身打造 “成长阶梯”,用系统化专业体系打破进阶壁垒。
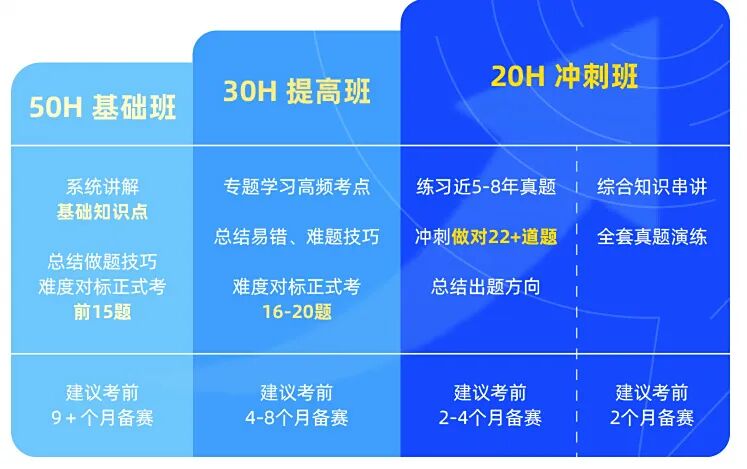
机构课程设置
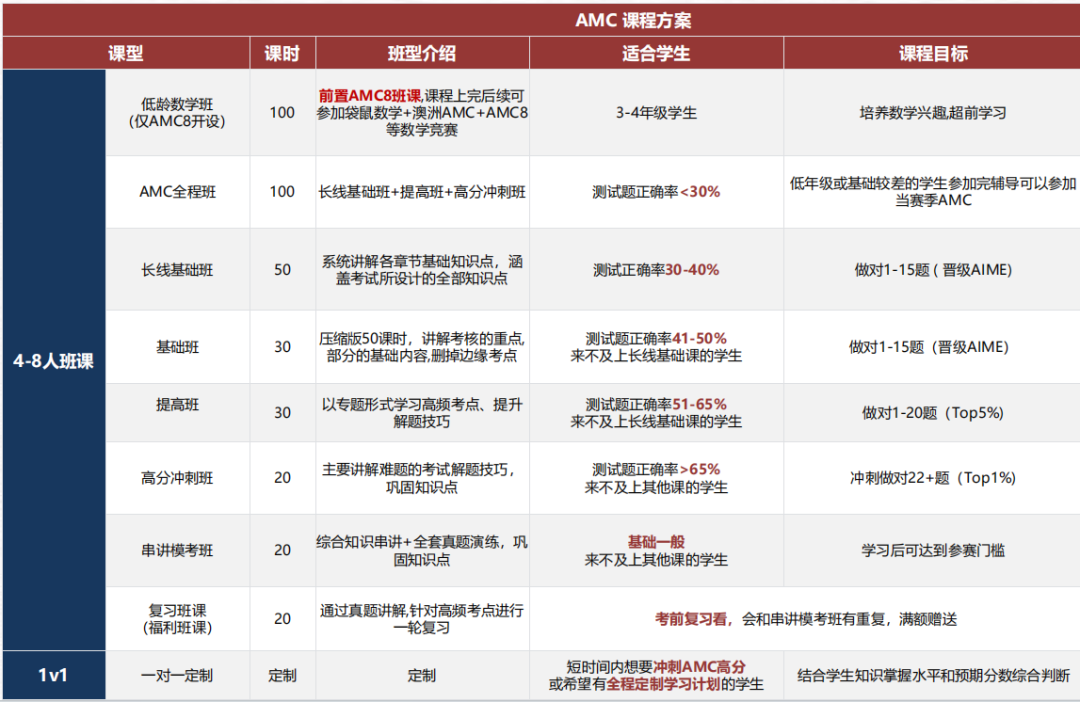
✅课程类型:4-8人小班/一对一授课
✅授课模式:线上/线下(深圳)同步开课
✅授课语言:中英双语教学/纯英文授课
机构师资
机构导师团队均为海内外名校背景,深耕 AMC 教学多年,不仅熟稔竞赛考点,更懂如何帮学生突破解题瓶颈;所带学生 AMC 获奖率超 91%,大批学员成功冲刺高分奖项!
机构课程亮点
💡运用学习金字塔:鼓励学生主动学习,做学习的“主人”
💡设置翻转课堂:课前督促学生复习上节课内容,课中可在自习室或借助classin等教学工具,提前预习;课后设置学生提问、讨论等环节。
💡贯彻费曼学习法:结课环节邀请学生从刁钻的角度“为难对方”
💡以赛代练:延伸学习校内课程,一门课程提高两门成绩。
💡学真正的数学:学习培养数学思维
💡培养深度思考:带来成绩巨变