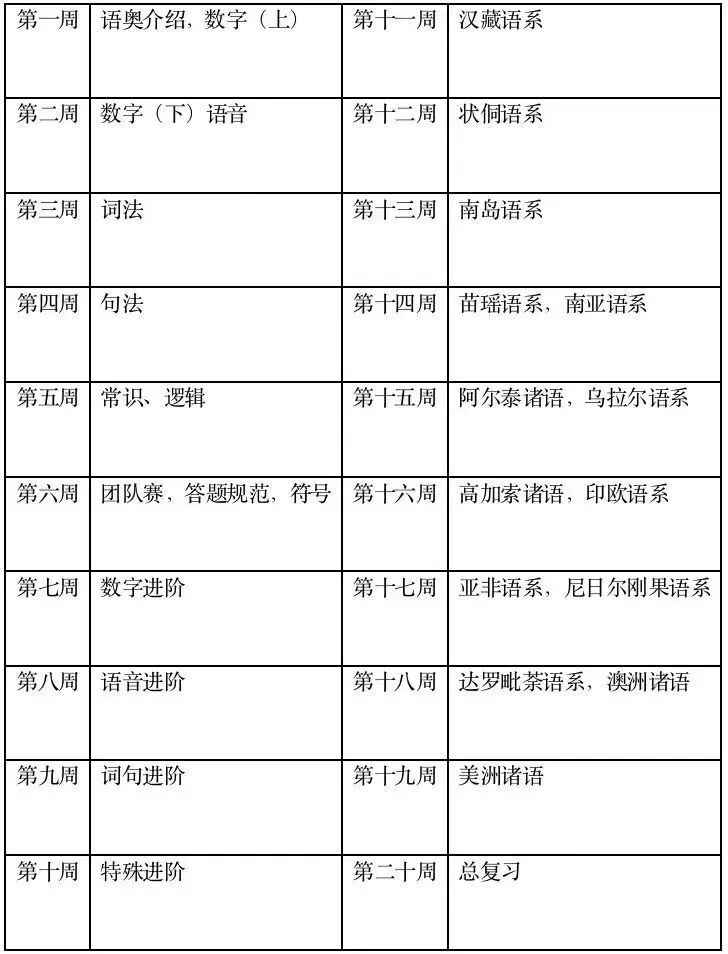
IMMC作为国际教育活动,在成立之初即明确自己的宗旨和初心是推动数学建模教育,培养学生的数学核心素养和科技创新能力;要申请理工科专业的同学可以重点关注一下该竞赛,想要参加的同学也可以尽早咨询报名,合理规划学习时间!
目前,2026国际数学建模竞赛IMMC秋季赛已经开启报名!想参加的同学们可以开始准备啦~
你和你的小伙伴应该如何准备呢?参加IMMC数学建模比赛的优势有哪些?接下来将给大家详细介绍一下这个竞赛~
什么是IMMC国际数学建模挑战赛
国际数学建模挑战赛 The International Mathematical Modeling Challenge,简称IMMC,是一项面向全球中学生的国际性新型数学建模竞赛。
国际数学建模挑战赛(IM²C或IMMC)在2014年创办于美国波士顿,其创办机构是美国数学及其应用联合会(COMAP)和香港儒莲教科文机构(NeoUnion)。来自世界各地的参赛团队经过国家/区域赛的选拔,进入国际赛程;在国家/区域与国际层面,皆有机会获取各级奖项。
中华区IMMC每年在香港举办。

官方网站:https://istem.info/
参加数学建模比赛的优势有哪些?
01、建模竞赛相比科研,对大部分学生友好
IMMC强调团队协作,参与解决现实问题的科研过程,项目题目没有标准答案。
数学建模比赛大都可以组队参加,在组队的过程中,同学们各有擅长的方向,并不是只有数学很强的人才能参加。数学建模是构建数学与其他学科之间的桥梁,涉及的领域远远超出了理论数学的范畴,工程技术、自然科学、经济、管理、金融、生物、商业分析等这些专业基本都和数学建模相关。
02、建模竞赛适用性广,比赛体现出的能力及知识对于很多申请专业都能用得上
数模竞赛的比赛内容一般包括建模、编程还有论文写作三个部分,主要考察参赛者 查阅文献、数学算法模型建立、编程软件求解问题、论文写作、团队合作等能力。也就是说,只要你申请的专业对这些能力有要求,都可以通过数学建模参赛经历来体现。
数学建模竞赛=数学能力的提升+含金量高的赛事+综合能力的培养。
03、对个人能力的塑造是全方位
总体上,对于个人它既需要你有基础牢固的专业知识,也要求你对其他学科有所涉猎,并且要会把所学的知识灵活运用在实际中,而不只是停留在理论。此外,对于你的想法,如何对其进行实现,如何编程以及如何写出一手漂亮的文章使得别人可以读得毫不费力,这些都需要每个人进行练习。也就是说,建模对于个人能力的塑造是全方位的自主学习,编程实现,结果描述,论文呈现等。
IMMC国际数学建模挑战赛比赛规则

1、面向学生:
参赛对象为中学生(7-12年级)。 每支参赛团队须由来自同一所学校的 2-4 名同学组成(队员学籍为同一所中学),且须有来自该校的至少 1 位教师担任指导老师。 IM2C 对每所学校报名的团队数目不设限额
2、比赛流程:
IMMC竞赛,分为区域赛、国际赛和国际赛答辩三个部分,各团队需要通过区域赛选拔至国际环节,最终参加国际赛答辩。
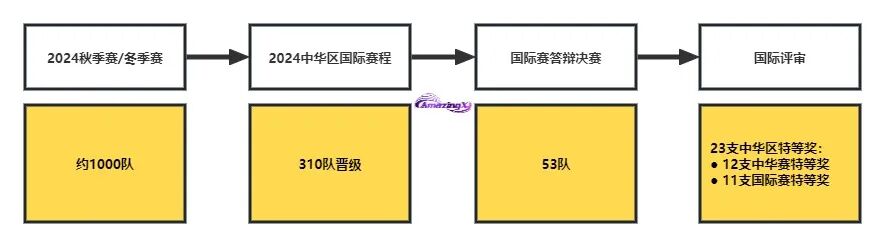
参赛者需要在在连续96小时之内完成并提交一篇数学建模论文,命题论文与自主选题论文将分开评审,两类论文中成绩进入首约 20+%的团队,将自动获得晋级国际赛程的机会。
*来自中国大陆、台湾、香港及澳门的所有参赛团队都要先经过中华区域的选拔赛才有资格参加国际赛。
*中华区域的选拔赛分为秋赛季和冬赛季,参赛团队可参加任意赛季,以最佳成绩为准。
3、报名费用:
100美元/队
4、奖项设置:
IMMC的选拔流程包括中华区域选拔赛和国际赛两个阶段。中华区域选拔赛分为秋季赛和冬季赛两个赛季,参赛团队可自由选择参加任意一个或两个赛季。国际赛则要求参赛团队在连续的120小时内完成一篇数学建模论文。
奖项设置包括Outstanding特等奖、Finalist特等入围奖、Meritorious一等奖、Honorable Mention二等奖和Successful Participant成功参赛奖。
2026 IMMC比赛日程时间线
| 报名注册 | 秋季赛报名截止:
即日起至 2025 年 11 月 20 日 冬季赛报名: 2025 年 11 月 24 日至 2026 年 1 月 30 日 |
| 秋季赛/
冬季赛 |
2025 年 11 月 20 晚 8 时至 11 月 24 日晚 8 时(秋季赛)
2026 年 1 月 30 日晚 8 时至 2 月 3 日晚 8 时(冬季赛) |
| 国际赛 | 2026 年 3 月 4 日晚 8 时至 3 月 9 日晚 8 时 |
| 答辩决赛 | 2026 年 4 月下旬,香港 |
| 国际峰会 | 2026 年暑期,美国波士顿 |
数学建模论文评审标准参考:
数模论文的评审标准可以帮助我们有针对性地了解出色论文的特点,进而指导我们在建模和论文写作方面的努力。以下是数模论文的评审标准:
01、假设的合理性:
评审人员会关注你对实际问题所涉及的变量和因素进行的简化假设,并对这些假设的合理性进行解释。合理的假设能够准确捕捉问题的关键因素。
02、模型的创新性:
评审人员将评估你的模型是否具有创新性,是否展现出高中生团队的数学思维和潜力。你所运用的数学方法应准确无误,能够在解决问题时展现出独特的见解。
03、结果的准确性:
评审人员会要求你的模型结果与实际问题相符合,并对解决实际问题做出贡献。你的建模方法应具有一般的价值和意义,能够为类似问题的解决提供有启发性的思路。
03、表述的清晰性:
论文的结构应完整,逻辑清晰,语言流畅,表述规范。评审人员将关注论文的整体质量,包括论文的组织结构、段落间的过渡、术语使用的准确性、建模图片等方面。