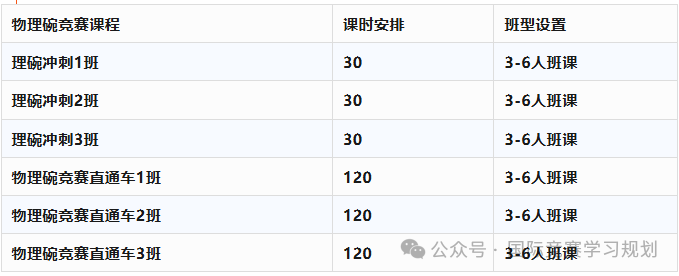
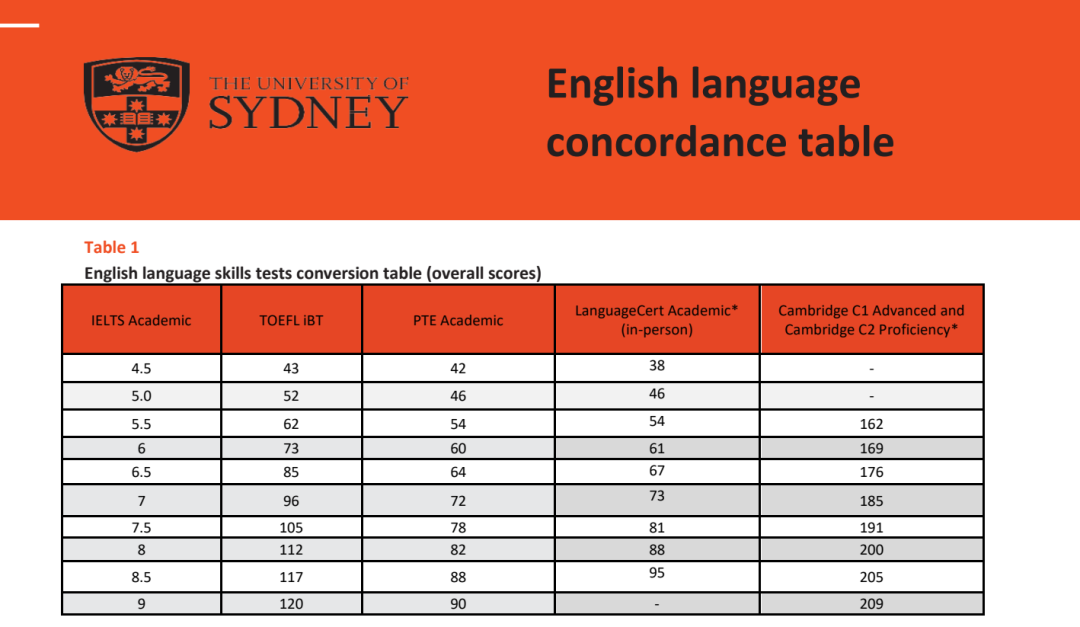
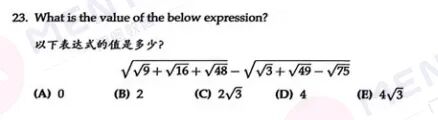01、招生要求
根据香港城市大学研究生院2026/27年度官方招生手册,申请生物统计学博士项目需满足以下要求:
1. 学术背景门槛
-持有认可大学的研究型高等学位;或
-持有授课式硕士学位;或
-持有一级荣誉学士学位或同等资质。
2. 英语能力证明
-托福最低分:纸考550分、网考79分、修订纸笔考59分(阅读、听力、写作总分);
-雅思最低分:6.5分;
-成绩有效期两年,申请提交时须仍在有效期内。
3. 香港博士奖学金计划(HKPFS)特殊通道
- 资助额度:每月津贴28,400港元(约3,640美元),年度会议及研究差旅津贴14,200港元(约1,820美元),最长三年;
- 额外福利:首年入学奖学金约105,800港元(约13,560美元),覆盖全年学费及校内宿舍费用;
- 第四年资助:四年制博士项目第四年,城大提供同等水平的学生津贴;
- 评选标准:学术卓越性、研究能力与潜力、文化多样性、沟通及人际交往能力、领导力与社会责任感;
- 流程:需先在研究资助局(RGC)在线系统注册获取参考号,再提交完整申请材料。
4. 申请材料清单
-官方成绩单及学历证明
-专业资格证书(如适用)
-发表论文记录
-两名学术推荐人报告
-研究计划书(部分学院要求)
-国际学生需提交学费支付能力证明
5. 选拔程序
-入围者需参加面试(现场、电话或视频会议);
-需提前联系潜在导师并获得同意;
-申请结果预计2026年5月公布。
02、研究方向

陈教授的研究版图覆盖理论统计与实际应用的交叉地带,近期成果呈现三大特征:方法学深度、跨学科广度、计算复杂性。
1. 时间序列结构突变检测
这是陈教授四十余年学术生涯的核心阵地。2025年发表于Statistica Sinica的"An Extreme-value Test for Structural Breaks in Spatial Trends"提出极值检验框架,解决空间数据趋势突变识别问题。该方法摆脱传统渐近分布依赖,通过极值理论构建检验统计量,适用于高维空间面板数据。2022年Annals of Statistics论文"Consistent Order Selection for ARFIMA Processes"则聚焦长记忆过程的模型定阶,提出的BIC准则在非平稳边界保持相合性。
2. 函数型数据分析的形状对齐技术
2024年Journal of the American Statistical Association刊发"Coefficient Shape Alignment in Multiple Functional Linear Regression",开创性地将系数函数形状而非数值大小作为知识迁移载体。该方法通过ReProcrustes对齐技术实现跨数据域的系数形状匹配,对协变量缩放具有不变性。此项工作直接启发了2025年提出的"Coefficient Shape Transfer Learning for Functional Linear Regression",在非渐近收敛速率与极小极大最优性层面建立理论保证,为医疗影像多中心研究提供新范式。
3. 自正则化推断理论
2021年Statistica Sinica论文"A self-normalized approach to sequential change-point detection for time series"构建的序贯检测框架,通过学生化统计量消除方差估计偏差。2025年Journal of Statistical Planning and Inference发表的"Self-normalized inference for stationarity of irregular spatial data"将该思想拓展至非规则空间数据,使用离散傅里叶变换处理协方差矩阵奇异性问题,在环境监测与流行病学中具有直接应用价值。
4. 空间统计与海洋学应用
研究活动贯穿"统计推断-物理机制-政策评估"链条。项目获得香港研究资助委员会资助,开展"Statistical Inference for Spatial Trends",将结构突变检测技术应用于海洋温度场、洋流速度场分析。该方法可识别气候变化背景下的海洋生态系统突变节点,为区域渔业政策提供统计依据。
5. 风险管理与统计金融
作为International Journal of Theoretical and Applied Finance的主编,陈教授将时间序列前沿方法引入金融风险度量。2023年Scandinavian Journal of Statistics刊发的"Nearly unstable integer-valued ARCH process and unit root testing"研究整数值ARCH过程的近不稳定区域,揭示高频金融计数数据的波动聚集新特征。
6. 高维时间序列协整理论
2023年Statistica Sinica论文"COINTEGRATION RANK ESTIMATION FOR HIGH-DIMENSIONAL TIME SERIES WITH BREAKS"突破传统协整分析维度限制,引入稀疏正则化处理断裂点,为基因组学中的多组学时间序列整合分析奠定理论基础。
03、有想法
基于陈教授的方法论积累与生物统计学系研究生态,申请者可在以下方向设计具有可行性与前沿性的博士课题:
构想一:可穿戴设备生理信号的自正则化变点检测系统
技术路线:整合陈教授自正则化检验框架(2021, 2025)与系内可穿戴设备数据研究基础(见2025年THE报道)。针对心率变异性、血氧饱和度等高频生理信号,开发无需预设基线的序贯变点检测算法。核心挑战在于个体异质性导致的方差非平稳性,可通过构建subject-specific的自正则统计量解决。临床应用场景包括癫痫发作前兆预警、哮喘急性发作预测。预期产出:算法嵌入智能手表终端,实现实时预警;理论层面证明该检验在局部备择假设下的渐近功效。
构想二:多中心医疗影像数据的系数形状迁移学习
技术路线:直接拓展陈教授函数型回归形状对齐工作(2024 JASA, 2025 arXiv)。针对阿尔茨海默病MRI影像数据,不同扫描仪厂商导致影像强度分布差异,传统迁移学习假设系数整体同质的限制过强。新框架仅需源域与目标域的系数形状同质,通过Procrustes对齐后,利用源域数据增强目标域模型估计。关键技术包括:(1)三维图像的函数型主成分表示;(2)基于核平滑的形状对齐算法;(3)数据驱动的信息源域筛选程序。该研究可解决罕见病影像数据稀缺困境。
构想三:环境健康风险的时空结构突变贝叶斯模型
技术路线:融合陈教授空间趋势突变检验(2025)与系内贝叶斯分层模型研究优势(见招生手册)。构建时空交互的贝叶斯分层模型,监测PM2.5浓度与呼吸系统住院率的关联强度时空演变。创新点在于引入结构突变先验,允许关联强度在未知时空节点发生跳跃。可逆跳跃MCMC算法用于后验抽样,计算负担通过伪边际似然方法缓解。政策应用:识别空气污染健康效应的敏感区域与关键时间窗口,为精准环境规制提供证据。该方向契合联合国可持续发展目标(SDG 3, 13)。
构想四:金融高频交易数据驱动的传染病传播风险评估
技术路线:嫁接陈教授整数值ARCH模型(2023)与系内图神经网络流行病预测研究(2025 arXiv)。将城市间人口流动视为"金融交易",构建整数值自回归条件异方差模型捕捉感染病例数的波动聚集性。结构突变检测用于识别防控政策实施节点,协整分析刻画城市间长期传播依赖关系。数据来自移动运营商脱敏迁徙数据与官方病例通报。预期贡献:揭示隐性传播链,评估非药物干预措施的统计显著性。