美国高中数学单词有哪些重要知识点

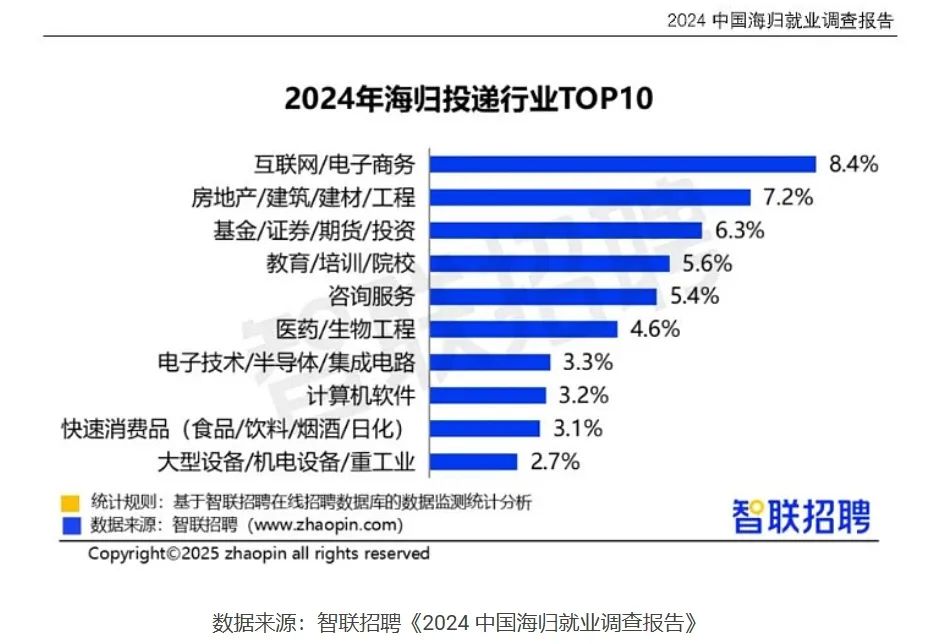
文章内容摘要：本文旨在深入探讨美国高中数学中的重要单词和概念，帮助读者更好地理解这些术语的含义及其应用。具体内容包括1、基础数学术语，涵盖加减乘除等基本运算；2、代数相关词汇，介绍变量、方程等基本概念；3、几何学术语，讲解形状、角度及面积等相关词汇；4、统计与概率术语，分析数据和概率的关键概念；5、三角函数词汇，解释正弦、余弦等三角函数的重要性；6、微积分基础词汇，简要介绍导数和积分的基本概念。通过这些内容，希望读者能够掌握美国高中数学中的核心单词，为今后的学习打下坚实基础。

一、基础数学术语

基础数学是所有高级数学学习的根基。在美国高中数学中，一些常见的基础术语包括加法（Addition）、减法（Subtraction）、乘法（Multiplication）和除法（Division）。这些运算不仅是计算的基本方式，也是解决各种数学问题的前提。

• 加法是将两个或多个数相加以得到总和。例如：2 + 3 = 5。
• 减法则是从一个数中减去另一个数，以得到差值，例如：5 - 2 = 3。
• 乘法是一种重复加法，用于快速计算相同数值的总和，如：4 × 3 = 12。
• 除法则是将一个数分成若干份，例如：12 ÷ 4 = 3。

掌握这些基本运算后，可以更好地理解后续复杂的数学概念与应用。

二、代数相关词汇

代数是美国高中课程中不可或缺的一部分。代数涉及到变量（Variable）、方程（Equation）以及表达式（Expression）等重要概念。

• 变量通常用字母表示，如x或y，它们可以代表任何数字。在代数中，通过操作变量来寻找未知量。
• 方程是一种包含等号的表达式，例如：2x + 3 = 7。这类方程可以通过求解找到未知变量的值。
• 表达式则是由数字和变量组合而成，但不包含等号，如：3x + 5。理解如何操作表达式对于解决方程至关重要。

掌握代数相关术语后，可以有效地进行更复杂的问题求解，比如线性方程组或二次方程。

三、几何学术语

几何学关注空间中的形状与图形，其核心单词包括点（Point）、线段（Line Segment）、角度（Angle）以及面积（Area）。

• 点是几何学中的基本单位，没有大小，仅有位置。
• 线段由两个端点连接而成，是一条有限长度的直线。
• 角度则表示两条线之间的夹角，可以用度来衡量，如直角为90度。
• 面积用于描述平面图形所占据的空间大小，例如矩形面积计算公式为长×宽。

理解几何学术语有助于学生在实际生活中识别各种图形，并进行测量与计算。

四、统计与概率术语

统计和概率在日常生活中广泛应用，包括平均值（Mean）、中位数（Median）、众数（Mode）以及概率（Probability）。

• 平均值是所有数据之和除以数据个数，用于反映一组数据的一般水平。
• 中位数是在一组数据按大小排列后位于中间的位置，适合分析偏态分布的数据集。
• 众数则是出现次数最多的数据点，有助于了解数据集中最常见的信息。
• 概率用于描述某事件发生可能性的大小，以0到1之间的小数表示，例如掷骰子出现某个数字的概率为1/6。

掌握这些统计与概率相关术语，可以帮助学生在分析数据时做出更明智的决策。

五、三角函数词汇

三角函数在许多领域都有应用，包括物理学与工程学。常见三角函数包括正弦（Sine）、余弦（Cosine）和正切（Tangent）。

• 正弦函数表示一个直角三角形对边与斜边之比，是描述波动现象的重要工具。
• 余弦函数则表示邻边与斜边之比，在周期性运动中起到关键作用。
• 正切函数为对边与邻边之比，用于解决许多实际问题，如建筑物高度测量。

熟悉这些三角函数及其性质，有助于学生进一步研究更复杂的问题，如傅里叶变换等高级主题。

六、微积分基础词汇

微积分作为高年级课程的重要组成部分，其核心概念包括导数（Derivative）和积分（Integral）。

• 导数用于描述一个函数变化率，即瞬时变化速度。例如，如果y=f(x)，那么f'(x)即为y随x变化时瞬时变化率。

• 导出过程通常涉及极限运算；

• 导出的结果可以用于优化问题；

例如，在经济学模型中，通过导出可以找到最大利润点。

• 积分则用于计算曲线下方区域面积，是导数反向操作。例如，通过不定积分，我们可以得到原始函数F(x)。

了解微积分基础知识，对于学生未来学习科学技术课程至关重要，也能帮助他们进行更高层次的数据分析及建模工作。

七、总结

美国高中数学涉及众多专业术语，这些单词不仅构成了学生学习过程中必不可少的一部分，同时也为他们未来深入研究提供了坚实基础。从基本运算到复杂的微积分，每个知识点都具有独特的重要性。通过系统化学习并掌握这些单词，学生能够提升自己的逻辑思维能力，并在解决实际问题时游刃有余，为今后的学习打下良好的基石。

常见问题Q&A

美国高中数学课程主要包含哪些内容？

美国高中数学课程通常涵盖代数、几何、三角函數以及微积分。这些课程旨在培养学生逻辑思维能力，并为他们未来学习更多高阶课程做好准备。同时，还会涉及一些统计和概率相关知识，以加强学生的数据分析能力。

如何提高对美国高中数学单词的理解？

提高对美国高中数学单词理解的方法包括积极参与课堂讨论、多做习题练习，以及利用网络资源查阅相关资料。此外，与同伴进行交流也是一种有效的方法，通过讨论不同观点来深化理解。同时，可利用记忆卡片帮助记忆关键术语及其定义，从而强化记忆效果。

是否需要额外辅导来掌握这些数学单词？

对于一些学生来说，额外辅导可能会有所帮助。特别是在面对困难概念时，找专业老师进行针对性辅导能够提供更多指导。然而，自主学习也非常重要，通过课本、自学材料及在线资源，同样可以达到很好的效果。因此，根据个人情况选择合适的方法最为关键。