数竞高联究竟考什么？

数竞高联究竟考什么？用比较官方的说法是：考察学生在数学领域的创新能力、逻辑思维能力、问题解决能力等方面的能力。这种官方万能话术听起来很浮夸，也不够走心。那我们实际一点，具体来讲说说高联考试的考点范围。

高联一试考11道题（8道填空题+3道解答题），试卷难题略微高于高考。一句话进行总结：你可以把高联一试理解成最基础的数竞入门，也可以理解成更难的高考。其实说白了，这种难度的考试，它只是考察学生对于知识整理、归纳的一个过程。

如果你系统性的学过数竞，跟着教练刷了很多的题，那么高联一试对你来说几乎没有难度，你唯一可能丢分的地方，也只有第8道填空题和最后一道解答题了，客观来说，这两道压轴题，还是有一些强度的。有些二试考的还不错的同学，也有可能在这两道题上丢分。

一试的难或许不在题目本身，而在于考试时间太短。想要在80分钟需要做出11道题，平均7分钟一道，对于绝大多数参赛选手而言，在时间上都具有很大压力，包括当年全国第7的徐老师也是如此。

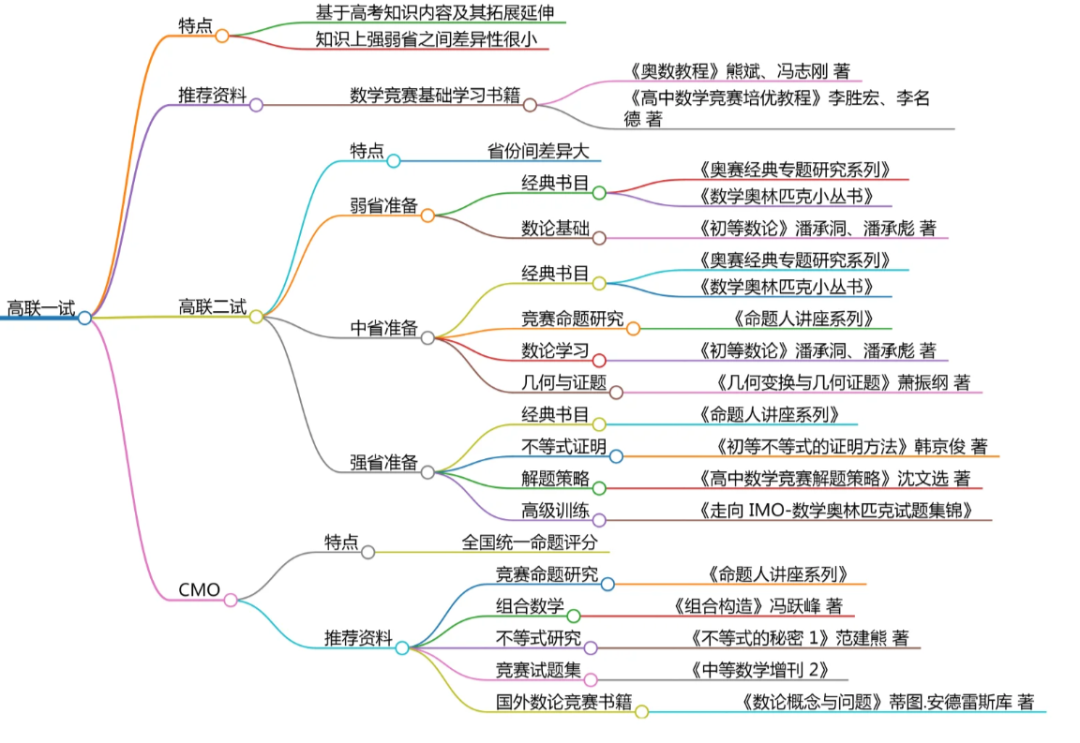
高联一试主要考察内容：“集合与函数”，主要注意一下函数最值问题，一般来说填空题会经常出现这一考点；然后是“数列”“三角函数”，当然这个也包括一些解三角形；再然后还可能会有“立体几何”，“解析几何”；此外，再就是“组合计数”，“复数”以及“向量”。

那么对于这些细小的知识板块，我们在学习时应注意哪些呢？本文结合前CMO国集大佬徐云昊老师曾在讲座中的分享，给今年及未来要参加数学竞赛的同学们如下硬核建议：

高联一试·数列

数列其实一般来讲呢，更多是研究一种递推数学。一试阶段，围绕递推的考察是比较多的，例如“通过递推求通项”，这是数列很重要的一个板块，比如说出题人给了你一个递推数列，你要知道这个递推数列，怎么去求通项；当然有的时候也需要我们判断，如何去求通项，这种题型是很常见的。

然后这个求通项的话呢，一般而言我们会有一些基础的这种分析策略，比较常见的是用“数列代换”，不断的去往这种简单的数列上面去靠。

除此之外呢，这种数列问题，我们也可以考虑使用“数学归纳法”，你只要能猜出来数列通项，基本上你是可以用数学归纳法去归纳这个通项的。

不过也有例外，因为有些递推数列，我们是不太能去求通项的，这种情况下，我们可以直接用数列去做一些性质。这个时候我们往往是有两种策略的：第一种，我们可以通过递推关系去化简表达式，说白了就是把这个递推关系带回去，带到数列里面，看能不能把表达式做一点点整理，就比如说本来是一个“和式”，我带一个替代关系出来，它说不定可以裂项，这样就能变成一个比较简单的式子；然后第二种策略，就是我们对这个递推关系，做一定的估计，尽管直接求解求不出来，但是我们可以大概取用这种递推关系去估一些“不等关系”或者“相等关系”。之后我们再用这个不等或相等的关系，再去做一些性质。

高联一试·三角函数

三角函数这个板块最大的一个特点：就是它公式很多，绕来绕去的，很容易在解题的过程中把自己给绕进去。所以在解三角函数题目的时候，我们第一个要注意的地方，是要熟悉这些公式。然后第二个要注意的，你在解题时要有对于三角函数变形的一个整体思路。

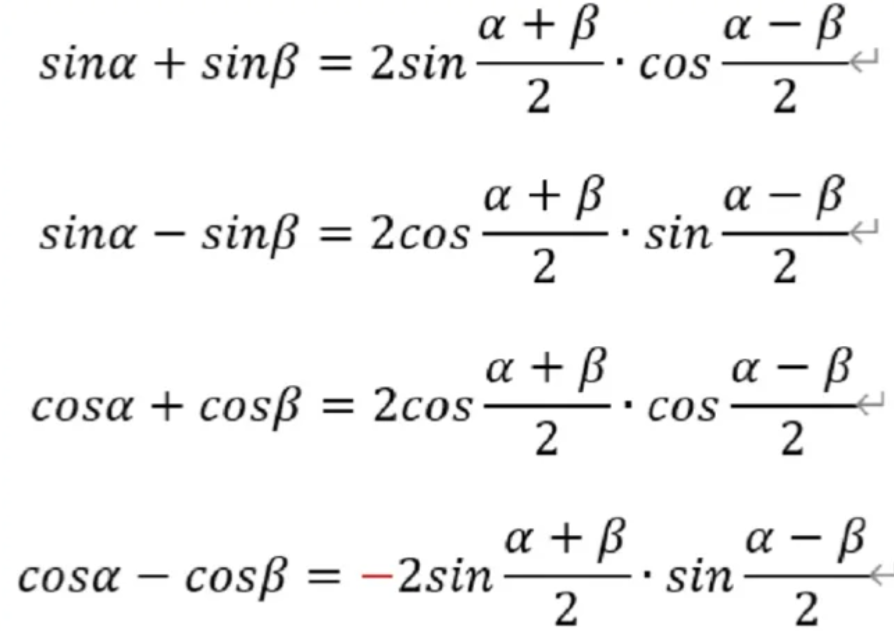
可能有些同学在初学三角函数的时候会发现，很多时候三角函数的公式，做来做去都是一样的。比如说，两个数的乘积可以积化和差，和差之后，它是不是又可以和差化积？然后，和差化积以后你又可以积化和差。实际上你做来做去，都是在做一个东西，这样子变形是没有太多意义的。所以这个时候，我们更多要考虑这个三角函数内部的代换，就是说你要考虑这个三角函数在一个变形过程中，函数里面的变量的变换情况。这个往往是高联一试考察的一个重点。

高联一试·立体几何

立体几何本身其实是很难的一个东西，因为很多处理是比较复杂的。不过幸运的是在高联一试的阶段，如果出了立体几何题，通常情况下不会特别难。一试阶段，立体几何的主要考查方向有两个：第一个是包含一些立体几何空间上的证明问题，这种题型最近几年考的比较少了，而且也基本不会出解答题，难度不大；因此，立体几何的第二个考察方向才是考生需要着重了解的，就是涉及空间量的一些计算。除此之外，对于立体几何，还有一个分析策略，就是尽可能去把一个立体几何平面问题，转换成平面几何，包括平时的期末考试、高考啊，去做这种立体几何分析的时候呢，我们也可以考虑去借鉴平面几何的分析策略：我们先假设把它当作一个平面几何，然后去找一些性质，找到性质后，我们再转换到立体几何里面。

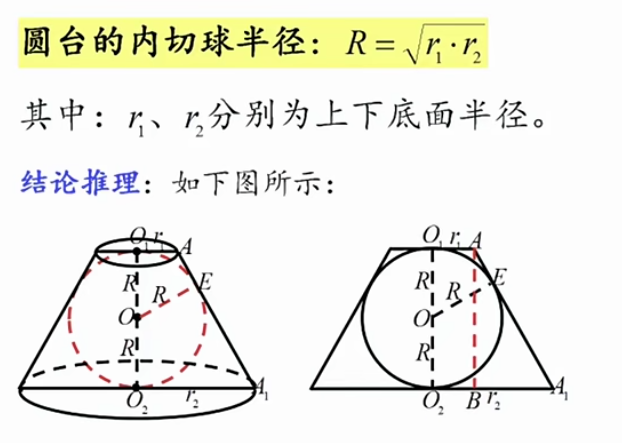
举个小例子：一个图形里面有一个内切球，那我们可以先把它做到内切圆，然后看有没有内切圆相关性质，如果有的话，那我们能不能再结合到内切球上面。其实说到底，数竞比赛考的不只是题，同时出题人也在考察我们的思维，所以类似这样的分析策略我们一定要熟练掌握。

高联一试·解析几何

在前面提到过，数竞高联一试由八道填空题和三道计算题构成。一般来说，计算题部分会围绕一些硬核知识点进行出题，例如解析几何。解析几何的关键点是什么呢？说白了，对于解析几何，多数同学都是能算的。

就是你一定要考虑如何才能算更快，这个才是做解析几何题的一个重点。解析几何很忌讳把问题算得复杂。而是应该清楚什么东西该求，什么东西不该求。有些东西我们能不能简单设出来，到后面再去消掉。“设而不求”是解决解析几何问题较为基础的技巧，也是解析几何中一种出奇制胜的解题技巧，运用得好可以达到四两拨千斤的效果。

比较典型的例子，当我们在求解圆锥曲线的题目时，经常需要将圆锥曲线与直线联立方程，并运用韦达定理算出“x1+x2”和“x1x2”，这实际上用的就是“设而不求”的方法。

在近几年的高联考试中，“设而不求”的解题技巧也逐渐深入到导数的题目中，在求极值点的过程中往往求不出导函数等于0的方程的解，这时候我们经常借助“设而不求”的方法虚设零点，并针对该零点进行单调性的分析，将复杂的问题简单化。

“设而不求法”在课内老师就应该教过，学竞赛的时候，各学校竞赛教练大概率还会再讲一遍，尽管如此，还是有很多同学掌握得不够扎实，运用起来更谈不上熟练。如果临近高联之时，你对解析几何知识模块还是掌握得一般，届时你可以重点练习一下这种解题方法（当然，这也是没办法的办法）。

高联一试·导数/不等式

导数/不等式，在数竞高联一试是一个非常重要的考点，如果出现，往往是便以一道大题的形式出现（极小概率会出填空题）。

在高联一试的阶段，导数考察的方向还是比较多的，比如可能和多项式函数建立起一定的关系，包括不等式也是，也可能和多项式函数建立起一些关系。不过在一试里，导数也好，不等式也好，考察的方式会更偏向于技术性，或者说技巧性。

就是说，对于某个式子，我们先要思考如何变形，之后再考虑如何求导。这种类型的题，算是高联一试里面相对来说比较难，但是也比较重要的一个重点内容。包括在强基考试里，这个东西也考了很多。例如零点问题、含参问题、最值问题。这些问题里面的很多操作，细节还是很多的，作为考生，我们一定要熟悉各种操作。

举一个典型的例子，就说e^s吧，这种量我们该怎么去处理，怎么样能让求导出的式子不是很复杂，作为数竞生，这些技巧都是需要我们去掌握的。

高联一试·函数

函数不仅性质多样，什么单调性、奇偶性计算也比初中数学更加复杂，综合性更强，而且更为关键的是，函数概念还很抽象。举一个具体的例子，很多数竞生在刚接触到y=f(x)这种表达形式的时候，基本上脑子都是懵的。

在高中阶段，函数是一个比较基础的知识点，但又很关键，如果函数概念这一块没学透，那么后面的一次函数、二次函数、三角函数、反三角函数、对数函数、指数函数、幂函数、偶函数、奇函数等内容，基本上也是学不会的。

早些年，大概在2015—2019年期间，高联一试对于函数的综合考察是非常常见的，考点多集中在函数的基本性质、幂指对函数、三角函数等。尽管最近两年高联对于函数的出题数量有所下滑，但竞赛生仍无法忽视函数这一考点。

高联二试呢

如果说，高联一试，考生还能嘻嘻哈哈，那么到了二试，绝大多数竞赛生绝对能体会到什么叫“江湖险恶”。高联二试只考四道大题，对应的四个知识板块分别是平面几何、代数、数论和组合。且每道题都是压轴中的压轴。二试主要考察知识点模块如下：

高联二试·平几

如果你是刚接触数竞的萌新，那么徐老师的建议是，大纲中的这些定理其实不用一个一个刻意去看，因为往后学习的过程中，你会很自然的接触到这些内容。相对来说，平面几何大致的出题方向可以分为两类问题。

第一类是直线型问题，第二个是圆类型问题。当然这两个也不是完全割裂的，因为很多直线型问题里面也会出现圆，同时有一些圆类型的问题也会用到很多直线型问题的处理方式。

徐老师个人认为学习几何的过程中，应着重注意两点：首先第一点，你要知道这种基础的图形结构，它的这些处理方式，这需要你熟知各种几何定理。当然了，也不只是定理，因为有些东西它本身也不是定理；然后第二个，就是要善于去做图形结构的分析，就是说你看到一个图的时候，你要知道，这个图它是怎么画出来的。

在高联二试中，有些涉及到平面几何的题，它的图乍看之下是很复杂的。但是再复杂的图形，它也是由一个一个简单的图形叠加到一起复合形成的。因此，你要做的，就是从局部尝试去拆解，把一幅复杂的图形拆分成多个简单的图形。

高联二试·代数

在高联中，代数部分的出题难度上下限很大，经常会出现去年很难，但是今年又特别简单的情况。一般来说，在高联这个阶段，代数的主要考点在于不等式和数列，这两部分内容涉及到的形式比较丰富，也容易和其它代数问题，甚至其它模块知识相结合。

这里有两点需要注意：第一，多项式理论虽然也被列入高联代数的考纲范围之内，但它的难度较大，在高联阶段基本不会考，只有到了CMO才会出现；第二，除了多项式理论外，其它内容高中课内都会学习，只不过高联对这一部分的难度要求、熟练度要求都更高。

基本上，在高联阶段，你代数这块，把不等式学好，大致就可以了。但如果你要准备CMO的考试，则还要着重学一下复数、多项式、函数方程，如果你的目标只到省一，然后走强基的话，那上面考纲这些内容适当了解一下就行。

高联二试·数论

不少同学在学习数论的时候，都表现得很畏惧。

数论这个东西其实是这样的，如果你刚接触数论，你会觉得数论是一个很模糊的模块，就是你会认为数论和你之前学的一些知识，不管是工具还是学习方法，或是处理方法，都不太一样。

但如果你数论入坑久了，学的还比较顺利的话，数论反而是一个做题使用率比较高的东西。而且数论是不太会出很难的题目，它如果出很难的题目，它也会和别的内容做挂钩，比如说和代数混在一起。数论更多的难点还是在于入手，多数人在前期学习数论的时候，都会有一种“不适应”的感觉，就是我前面说的“很模糊”，这个是正常的。

这是由于我们初中阶段，很多学校在数学教学中以代数和几何为主，教材里很少涉及数论内容，老师也很少讲，加之自己从前也几乎没怎么接触过数论，所以你会觉得数论异常难学。不过当你摸清数论的门槛之后，你会发现数论其实并没有想象的那么难，可能要比代数更容易学。

高联二试·组合

组合问题，在高联二试中往往是作为“压轴题”出现的，非常具有难度。

在高联的阶段，比较常见的组合问题可以归纳为两个类：第一类叫组合计数问题，是基于课内“排列组合”的部分知识，进行拓展和扩充；第二类叫组合杂题，包括组合最值问题、组合构造问题、对策与操作等几个主要类型。

在高联考试中，高联一试会考较复杂的分类计数，高联二试的考试一般以组合杂题为主，且难度很大，涉及范围广，形式灵活多变，对数学综合分析的能力要求也更高。关于组合杂题，我们在学习的时候要做到了解基本的组合原理，并以此为基础，拓展思考方法，积累常见的组合构造。

基础的组合原理有很多，并且理解起来也都不难，比如“抽屉原理”，国外叫“鸽笼原理”，类似这种概念的原理，理解起来是不难得，但真正的难点在于我们如何应用，如何根据题目构造出我们所需要的“抽屉”，也就是数学概念中的集合。

这其实是组合学习、组合训练核心想要解决的问题。此外，组合问题的难点还在于“杂”，因为除了“抽屉原理”外，组合问题的原理还有极端原理、容斥原理、算两次、染色与赋值法等。也就要求我们在面对组合难题的时候，要找到该题的切入点。这种切入点很杂，难以概括，不同背景的组合问题，切入点可能差别很大。