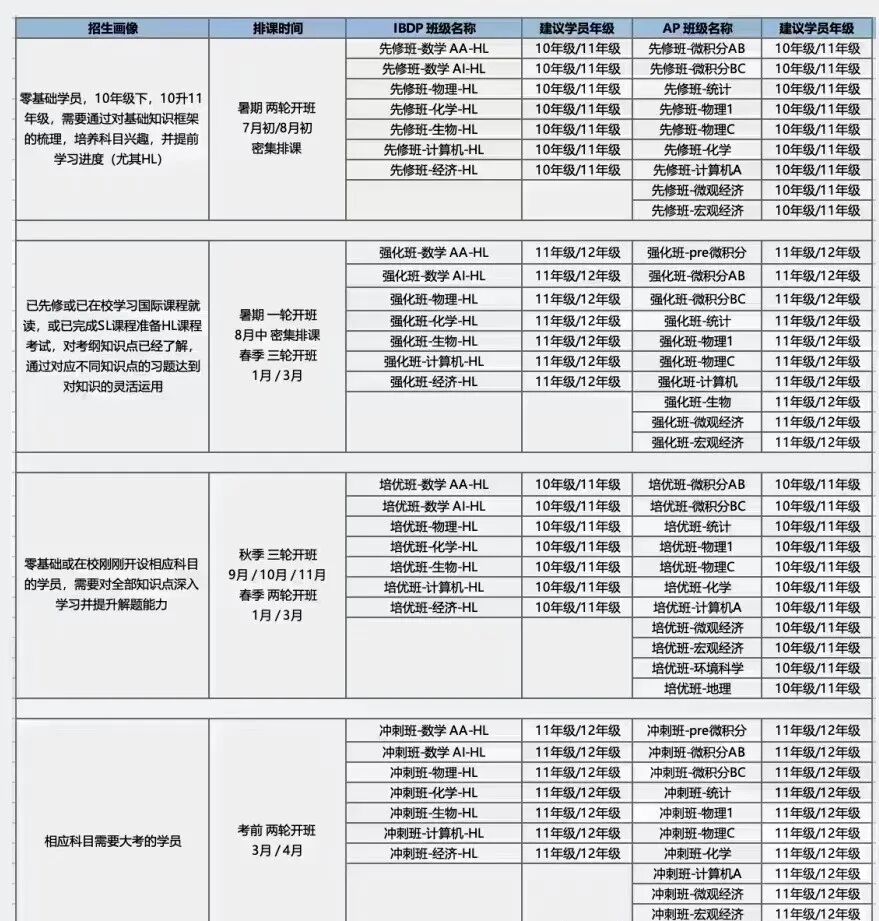
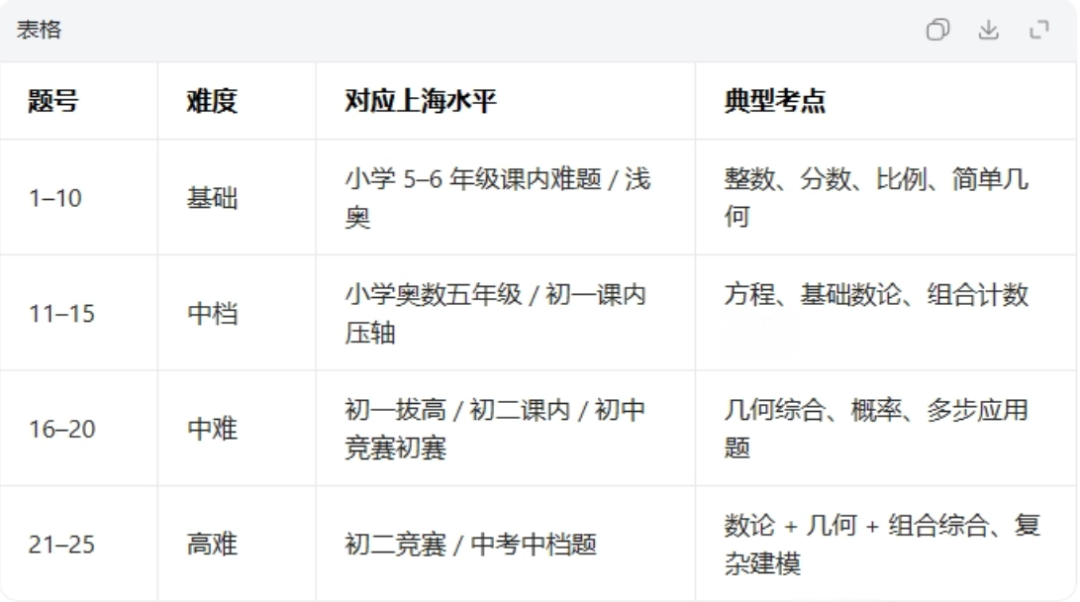
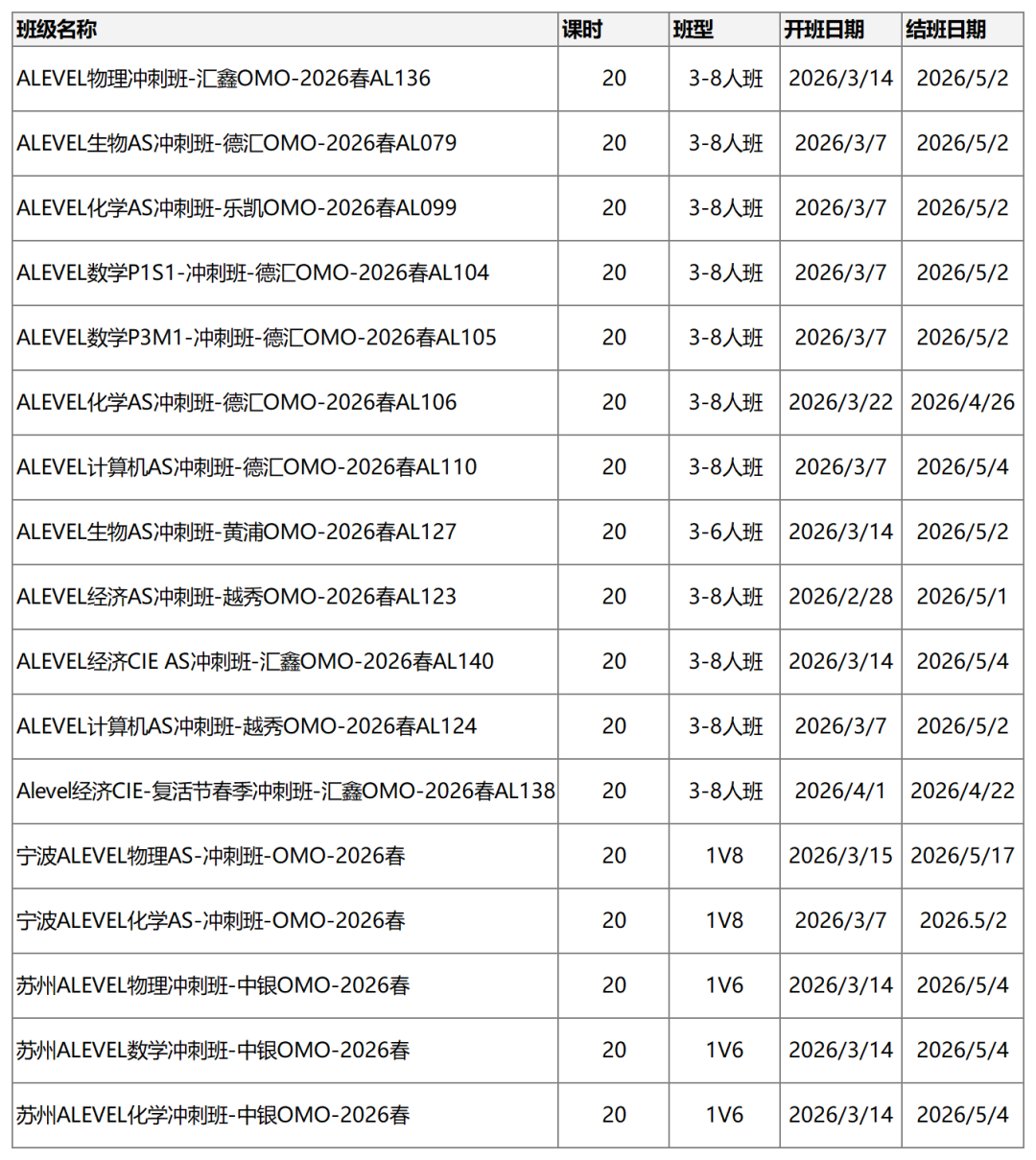
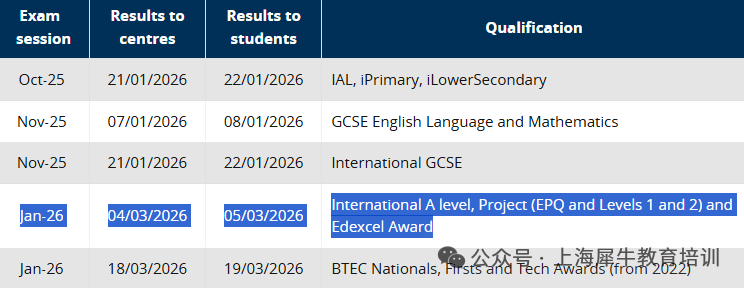
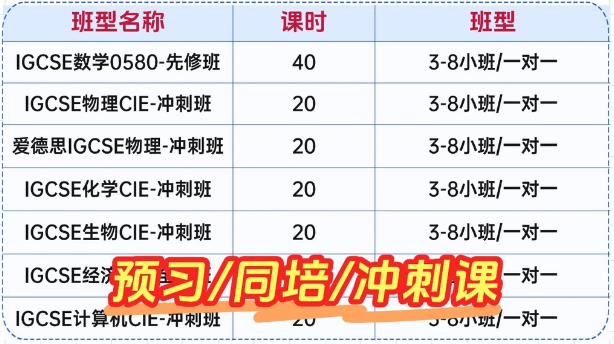
高中阶段进行数学科研是一个极好的探索方式,不仅能深化你对数学的理解,还能培养你的研究能力和学术素养。虽然高中生很难做出突破性的前沿贡献,但完全可以在合适的指导下,完成一个完整、有趣且具有一定创新性的研究项目。
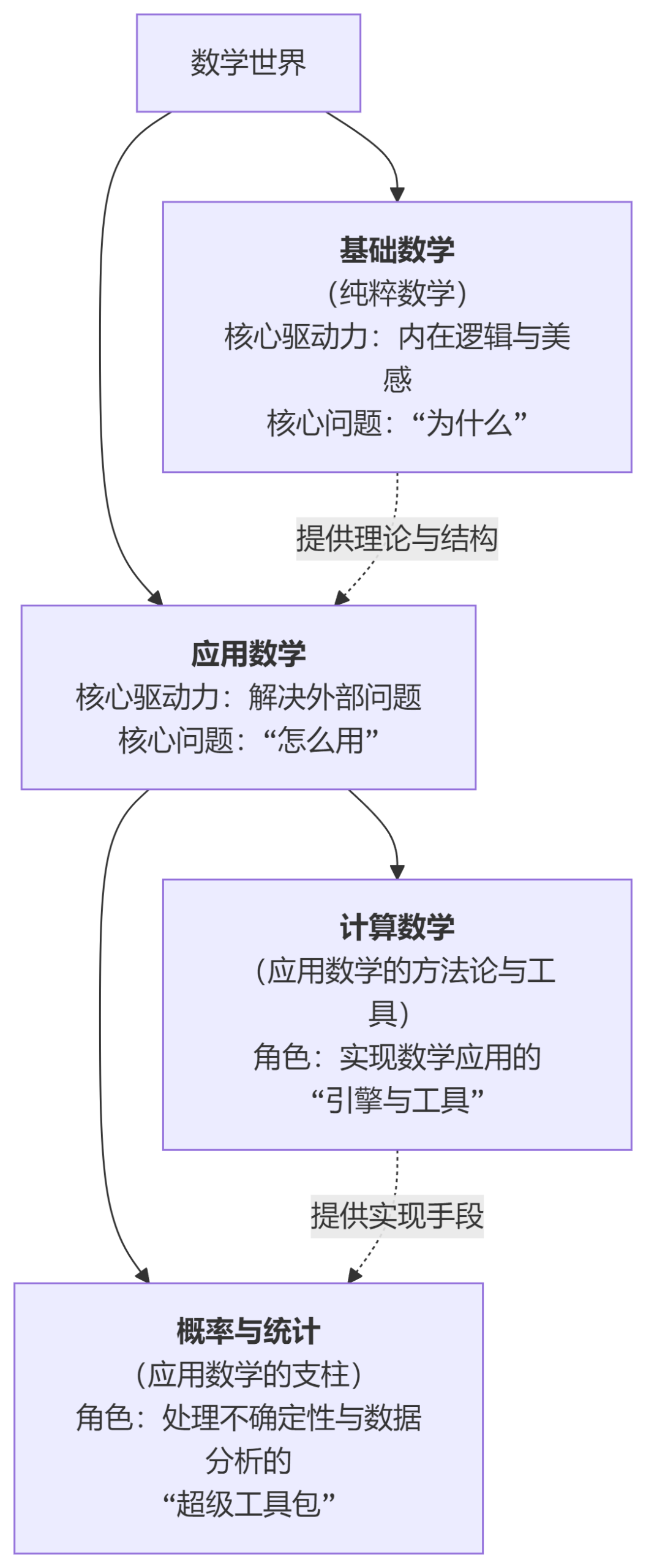
今天我们将以基础数学、应用数学、概率与统计、计算数学四个领域为例,探讨他们的关系,同时我们将通过课题案例,带你寻找自己的研究感兴趣~
01基础数学
高中生对于基础数学的研究通常不追求(几乎也不可能实现)原始的理论突破,关键在于“小题大做”,研究的价值不在于问题本身有多新,而是把一个问题研究透彻,展现学生应用和掌握高级数学工具的能力。
参考课题:多体约化矩阵到部分矩阵的满射和单射
研究以矩阵与线性代数理论为基础,结合组合数学与图论中的离散结构思想,研究多体系统约化矩阵的代数与组合性质。将引入图论中的邻接矩阵、拉普拉斯矩阵等作为重要实例,探讨矩阵的谱、秩与线性相关性在图和组合结构中的表现,并借助组合集合映射观点,分析多体约化矩阵与单体约化矩阵之间的映射关系,着重研究该映射在组合约束下的单射与满射性质,以及相关子集的构造与计数问题。
02应用数学
这是将数学工具应用于解决实际问题的领域,需要将现实问题转化为数学问题,并解释结果,非常适合喜欢跨学科研究的学生。
参考课题:基于应用数学方法的废气排放检测策略研究
随着社会对环境问题关注度的提高,大型能源企业如火力发电厂、炼钢厂等面临的环保压力日益增大。政府对废气排放制定了更严格的法规,企业也需通过有效的监测与管理来履行社会责任。在此背景下,本研究以废气排放检测为例,基于数学建模方法,运用线性规划、决策分析和博弈论等工具,探讨在资源有限条件下如何合理分配人力、物力和时间,在保障生产的同时控制排放量。
03概率与统计
这是一个极具应用价值且易于获得数据的领域,非常适合高中生。概率与统计是非常重要的应用数学分支,由于其方法论的特殊性和应用的广泛性,常常被单独列出,与应用数学并列。数据驱动,与现实世界联系紧密,能培养数据分析能力和批判性思维。
参考课题:“双减”政策背景下青少年素质教育培训产业的机遇
课题结合应用数学与计算机算法,研究“双减”政策下素质教育培训机构的动态变化与未来发展。通过收集与分析政策前后行业数据,构建统计模型并进行回归分析和模拟预测,量化评估政策影响及市场需求变化,进而预测市场规模与发展趋势。研究成果旨在为行业前景判断和政策优化提供数据支撑和决策依据。
04计算数学
研究数学问题的算法设计、分析和实现。它关注的是:如何把一个连续的数学问题(如求解微分方程、求积分)离散化,变成计算机可以处理的算法,并保证计算结果的精度、稳定性和效率。
参考课题:稀疏多项式插值算法的设计与应用研究
课题聚焦于计算数学核心领域的稀疏多项式插值算法研究,旨在解决当多项式大部分系数为零时的高效重构问题。学生将学习经典插值方法及其在稀疏场景下的局限性,重点探索利用稀疏性优化算法的设计与性能,并通过数值实验验证不同算法在采样复杂度和计算效率上的表现。课题结合理论分析与编程实践,培养学生针对特定应用场景(如信号处理、数据压缩)开发专用插值算法并评估其效果的能力。
这些课题可以参加哪些竞赛?
全球青年研究创新论坛(CTB)

全国青少年科技创新大赛


国际科学与工程大奖赛

除了参加各类竞赛,论文亦可投递各类期刊会议进行发表: