Precalculus预备微积分
AP 新科目 预备微积分AP Precalculus
开课目的
我们之前有提到IGCSE和MYP阶段数学尤其是函数部分,其实相对来讲是比较简单的,但是到了A-Level阶段、IBDP阶段也好,它对函数部分的讲解和要求一下难度就提上来了。
所以很多家长希望能够在IGCSE或MYP阶段去提前学或是加强数学的难度,那 Precal无疑是一个非常好的桥梁和过渡。一方面是Precal涉及到的知识点,在A-Level和IBDP阶段也非常重要,Precal的难度又高于IGCSE和MYP,学生学习这个部分的知识点能更好地为A-Level和IBDP做准备,也能更好的过渡和衔接到A-Level和IBDP。另一方面是Precal有全球统一的考试,能够更好的检测学生的学习成果,让学生在学习过程中有个目标感。
Precal的考察和难度比数学竞赛更接近A-Level和IBDP,所以很多想要通过数学竞赛来提升数学能力并为A-Level和IBDP做准备的同学,其实会发现数学竞赛的出题思路和难度对于大部分学生来说太难了,相反并不能帮助他们巩固基础知识点,应对A-Level和IBDP。
Precal正是这样的一个考试,可以帮助学生在MYP阶段、IGCSE阶段,把数学的级别稍微提高一点,不至于在学校学的都过于简单,然后到了A-Level和IBDP一下子难度提的特别的高。
因此我们比较建议,如果数学上想有一点追求,然后学生底子也不错,并且现在在IGCSE和MYP觉得数学太简单了,但是,竞赛来讲又太难,那么作为中间的一个过渡的课程 Precal就是一个非常好的选择,以及中间过渡。
学科内容

Universe Beyond
培养技能
科目旨在培养学生的以下3个专业技能:
Procedural and Symbolic Fluency
Multiple Representations
Communication and Reasoning
考题设置
具体考试的题目分布和考查方式类似 Calculus,分为MCQ(Multiple Choice Question)多选和FRQ(Free Response Question)简答两部分。
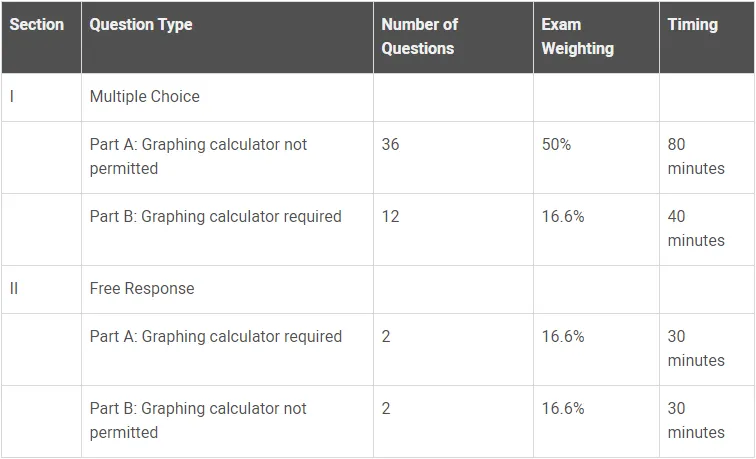
MCQ选择题共48题,其中前36题为不可使用计算器题目,分数占比50%,时长80min;后12题为可使用计算器题目,分数占比16.6%,时长40min。
FRQ简答题共4题,其中前2题为可使用计算器题目,后2题为可使用计算器题目。两项分数占比均为16.6%,时长均为30min。
考试的模块分布跟微积分一样,考试时间比微积分考试少15分钟, 但也是长达3个小时. 整体的题量会比微积分少.
采取的考试形式和AP Calculus整体比较相似.
Calculus具有一定难度,学生不能很好的过度到微积分的学习,所以Precalculus可以帮助学生先做一个铺垫,循序渐进过度到Calculus的学习,以便之后能够掌握好这项数学技能,应用到未来其他学科领域中。
计算能力要求
拿到5分的重中之重在于不能用计算器的前36道多选题,可见这门课对于学生的计算能力也是有相当的要求的。
数学课学习推荐
许多家长也是比较头疼:孩子们到底应该按照什么顺序、选择哪一门来读呢?
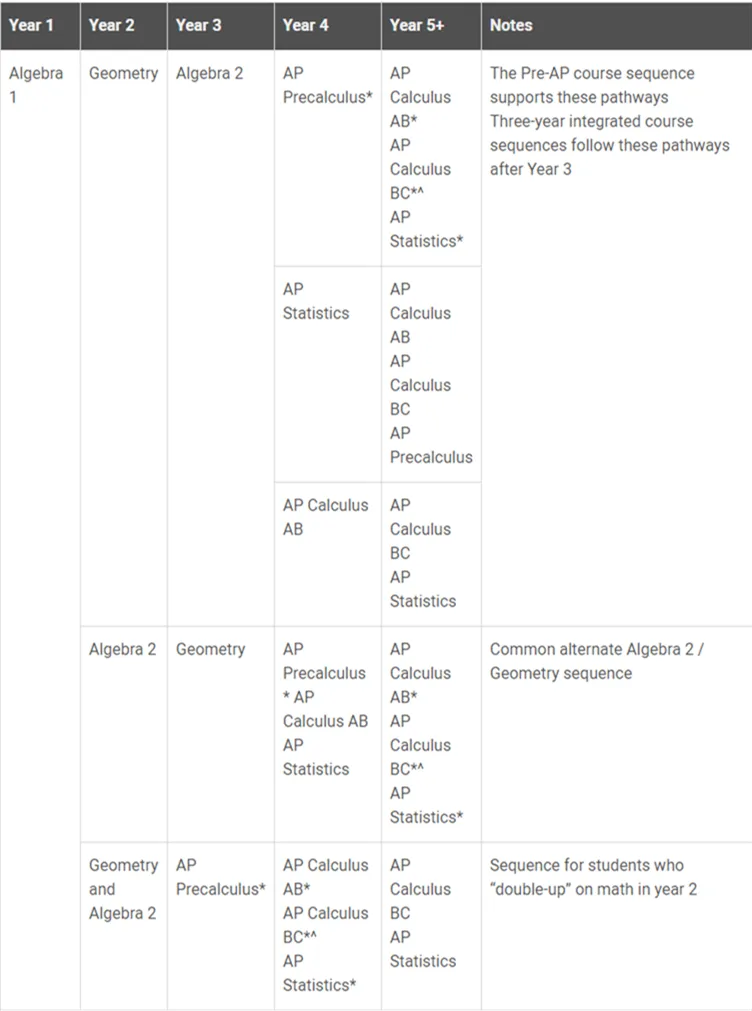
根据学生自己的学习情况,可以适当加快这一进程。在学完algebra 1、algebra 2与geometry之后即可学习precalculus。当然,对于程度比较好的同学,甚至可以直接学习 statistics或者calculus。
对于国内的同学们而言,一般9或10年级、甚至一些同学8年级的数学水平就完全可以学习precalculus的程度了,故而对于同学们来说,与其去冒险学一门比较难的calculus或浪费时间去学习对自己的程度来说相对比较简单的数学,作为一门衔接课程来学习precalculus是非常不错的选择。
欲学习的知识点
In detail, precalculus deals with:
Sets
Real numbers
Complex numbers
Solving inequalities and equations
Properties of functions
Composite functions
Polynomial functions
Rational functions
Trigonometry
Trigonometric functions and their inverses
Trigonometric identities
Conic sections
Exponential functions
Logarithmic functions
Sequences and series
Binomial theorem
Vectors
Parametric equations
Polar coordinates
Matrices
Mathematical induction
Limits