物理竞赛进阶思维之你可以学会的非惯性系第三弹

一、什么是非惯性系

在课内的学习中，大家可能会看到这样的说法：在惯性系里，牛顿运动定律成立。然则什么是惯性系，以及为什么在非惯性系中，牛顿定律不成立，却鲜有涉及，因为这并不是课程大纲中需要掌握的内容，即使在一些初级的竞赛中也不会有相关的题目。

但对于一些较难的竞赛，或者是想要加深对物理现象的理解，还是有必要学一下非惯性系的内容。这里我们直接给定非惯性系的定义：有加速度的参考系！这里的加速可以理解为直线运动的加速度，也可理解为圆周运动的加速度。

二、惯性系 VS 非惯性系

转动的非惯性系

前面讲述的所有内容，给定的非惯性系均有一个平动的加速度，但我们也曾指出，只要有加速度就是非惯性系，因此我们来考虑另外一种非惯性系—转动。

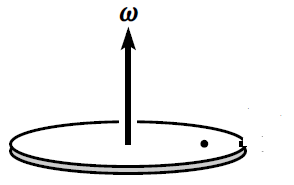
设想给定一个转盘，角速度为ω, 一个小球放在盘子上，随着盘子一块转动（或者说小球和盘子相对静止），小球做的是圆周运动，那根据课内的知识，可以做出受力分析图如下，其中f为盘子表面给小球的静摩擦力，也是小球所需的向心力

以地面为参考系（惯性系），可写出牛顿定律

ΣF=ma

f=mω²R

现在我们以转盘为参考系（非惯性系），那修正受力分析图如下：

其中F'即为惯性力，或者大家听到的另一种说法—离心力！由于a为向心加速度指向圆心，而离心力的方向和它方向相反，因此指向外侧。这也是大家在学圆周运动的时候，老师会再三强调，不要说离心力，只说向心力就可以，因为离心力是在非惯性系的背景下才会考虑的！

在转盘上的人看来，小球和他自己一样也是没有动的，我们写出牛顿定律：

ΣF=ma'

F'-f=ma'

mω²R-f=m*0=0

其中a'是小球相对于转盘的加速度，由于相对静止，所以a'=0, 最后求得f=mω²R, 这和之前用传统的方案所得结果一致。