一、什么是非惯性系
在课内的学习中，大家可能会看到这样的说法：在惯性系里，牛顿运动定律成立。然则什么是惯性系，以及为什么在非惯性系中，牛顿定律不成立，却鲜有涉及，因为这并不是课程大纲中需要掌握的内容，即使在一些初级的竞赛中也不会有相关的题目。
但对于一些较难的竞赛，或者是想要加深对物理现象的理解，还是有必要学一下非惯性系的内容。这里我们直接给定非惯性系的定义：有加速度的参考系！这里的加速可以理解为直线运动的加速度，也可理解为圆周运动的加速度。
二、惯性系 VS 非惯性系
转动的非惯性系
前几期我们介绍了两个惯性力，一个与平动相关，另外一个是离心力，现在我们再给出第三个惯性力-科里奥利力。
依然考虑之前的模型，一个转动的盘子上，放了一个小球，假定盘子是光滑的，那么不难做出受力分析，小球所受重力与盘子给的支持力互相平衡，水平无任何力。因此在地面上的人看来，小球原地不动。
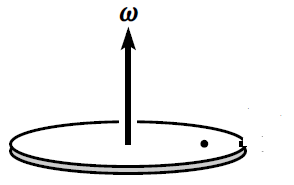
但以盘子作为参考系呢？此时我们指出：小球相对于转动的参考系在运动，会受到新的惯性力—科里奥利力Fcori
Fcori=−2m ω×v
其中的ω为角速度矢量，v是物体相对于参考系的速度。ω×v中的乘号代表向量的叉乘运算，其方向是大家需要用右手定则来确认的，此处不再赘述。
依然，大家不需知道科里奥利力这个表达式的来源，其推导过程远超高中阶段的物理，我们学会应用即可。做出本题对于小球的受力分析图（在转动参考系下）如下
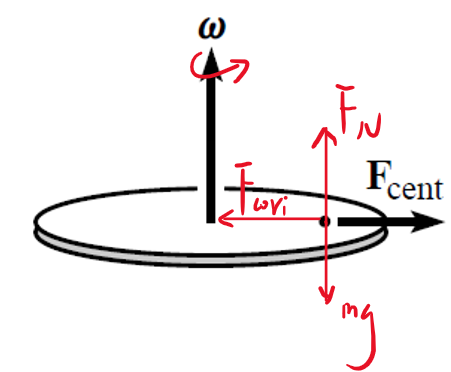
其中Fcent是前面讲到的离心力(Centrifugal force)，而Fcori则是由于小球相对于参考系运动，所受的科里奥利力（Coriolis Force），其方向判定可以这么来看：先用右手定则找ω×v的方向，然后把这个方向反转即可（因为有负号），大小可以写做Fcor=2mωv=2mω2r,
不妨再给出受力分析图（俯视图）
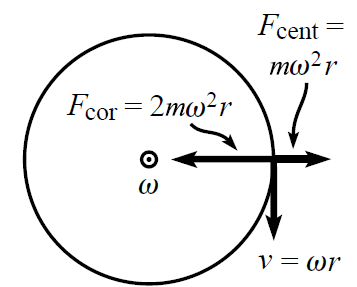
之后我们在水平方向写出牛顿第二定律：
ΣF=ma'
Fcor−Fcent=mω2r=ma'
其中a'是这个小球相对于盘子的加速度，解得a'=ω2r，这和向心加速度的表达式一致，此时可以这么理解，物体相对于盘子做顺时针方向的圆周运动。
三、结语
今后做题的时候大家需要先确定选取的参考系，然后做受力分析，对于非惯性系还需要加上相关的惯性力，之后列牛顿运动定律来求解即可。
【竞赛报名/项目咨询+微信：mollywei007】
