拒绝二选一：规划得当让AMC10/12与课内数学相互成就

初高中数学是数学学习的“根”，AMC10/12是数学能力的“枝”，唯有根扎得深，枝才能长得壮。

在数学学习的道路上，很多学生和家长常常面临一个看似两难的抉择：是扎实学好课内数学，还是投入时间备战AMC这类国际数学竞赛？

事实上，初高中数学与AMC10/12并非对立关系，而是呈现出【基础与升华、规范与创新、应试与素养】的辩证统一。前者构建知识体系的基石，服务于升学与基础能力培养；后者拓展知识的应用边界，聚焦思维进阶与问题解决能力的选拔。

定位与考察：规范基础 vs 灵活拓展01

初高中数学作为国家课程标准下的基础性学科，覆盖代数、几何、概率统计、函数等核心模块，具有鲜明的系统性与规范性。

它的考察重点在于知识的全面性与扎实度，要求学生掌握公式推导与概念定义的本质，注重解题的规范性与步骤完整。题型相对固定，答案唯一，目标直指中考、高考等选拔性考试。

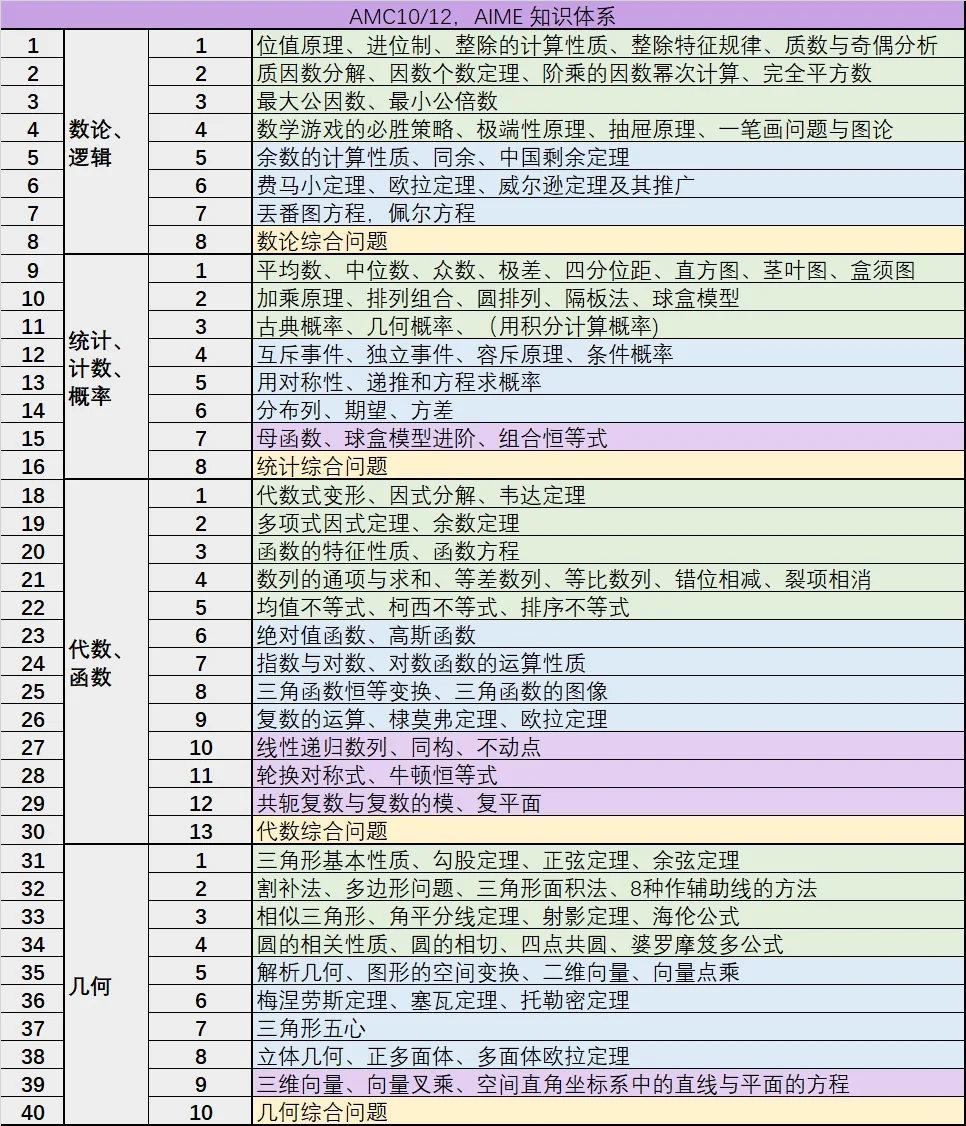
而AMC10/12作为面向全球高中生的数学竞赛，则以【选拔数学潜力者】为核心目标其内容虽以初高中数学为基础，却延伸至数论、组合数学、高级几何等领域，甚至触及部分大学预科内容，具有强烈的拓展性与灵活性。

AMC的试题尤其注重思维的灵活性与逻辑推理能力，鼓励“巧解、速解”，答案唯一但解题路径多元，旨在区分学生的数学潜力与拓展能力。

内容关联：基础同源，进阶互补02

AMC10/12与初高中数学在知识体系上高度同源。几何部分以初高中几何定理为核心，概率统计部分围绕基础概率与图表分析展开。

AMC的几何题更侧重定理的综合应用与交叉解题，概率题则增加了计数原理与条件概率的复杂场景。

可以说，初高中数学是AMC10/12的“知识基础”，没有扎实的课内基础，AMC的拓展便无从谈起；而AMC训练则是初高中数学的“能力提升”，能反向深化对课内知识的理解与应用能力。

学习路径：循序渐进，闭环提升03

两者在学习过程中形成天然的递进关系，构成【基础巩固-拓展提升】的有效闭环：

初中阶段完成代数与平面几何基础后，可接触AMC8培养兴趣与拓展思维；高中低年级在学习函数、立体几何的同时，可备战AMC10，训练课内知识的灵活迁移；高中高年级深化三角函数、导数等知识后，可冲击AMC12，并通过其数论、组合模块完善数学体系。

这种连贯性避免了课内与竞赛的脱节，形成【以课内支撑竞赛，以竞赛反哺课内】的良性循环，使复杂函数、几何综合等课内难点更易突破。

学习方法：系统建构 vs 思维突破04

✅初高中数学学习强调系统性：深入理解概念与公式推导逻辑，通过分层刷题巩固知识、强化应用、突破瓶颈，注重解题规范与步骤严谨。

对应的培训侧重【知识点全覆盖+解题技巧标准化】，帮助学生掌握应试核心能力。

AMC10/12则更注重拓展性与思辨性：主动学习数论、组合等课内延伸内容，掌握数形结合、分类讨论、逆向思维等竞赛技巧，并重视错题思路复盘与限时节奏训练。

AMC10/12培训侧重【思维引导+难题突破】，强调探索解题路径的过程比答案本身更重要。

协同规划：根深才能枝壮05

脱离课内基础的AMC训练如同“空中楼阁”，而忽视AMC拓展的课内学习则易陷入机械刷题的困境。但两者终极目标一致：培养学生逻辑推理、数学建模、运算求解与直观想象的核心素养。

低年级学生应以课内数学为核心，同步接触竞赛内容培养兴趣；高年级则在巩固课内基础上，针对性突破AMC难点，实现能力升级。

数学教育的意义不仅在于应对考试，更在于通过系统训练与思维拓展，培养学生受益终身的分析与解决问题的能力。

初高中数学与AMC10/12的辩证统一，正为这条成长路径提供了坚实的基础与开阔的视野。