很多同学在备考AMC10/12的时候一定会有这四个问题:
AMC10/12的题型风格有怎样的趋势?
AMC10/12都会考察哪些知识点?
AMC10/12难题能不能快速找到思路?
距离AMC10/12考试还有4个月时间了,如何科学备考AMC10/12?
AMC10/12提分攻略来啦! 4个月如何获奖?老师为大家整理和分享以上问题的答案,快来查看吧!
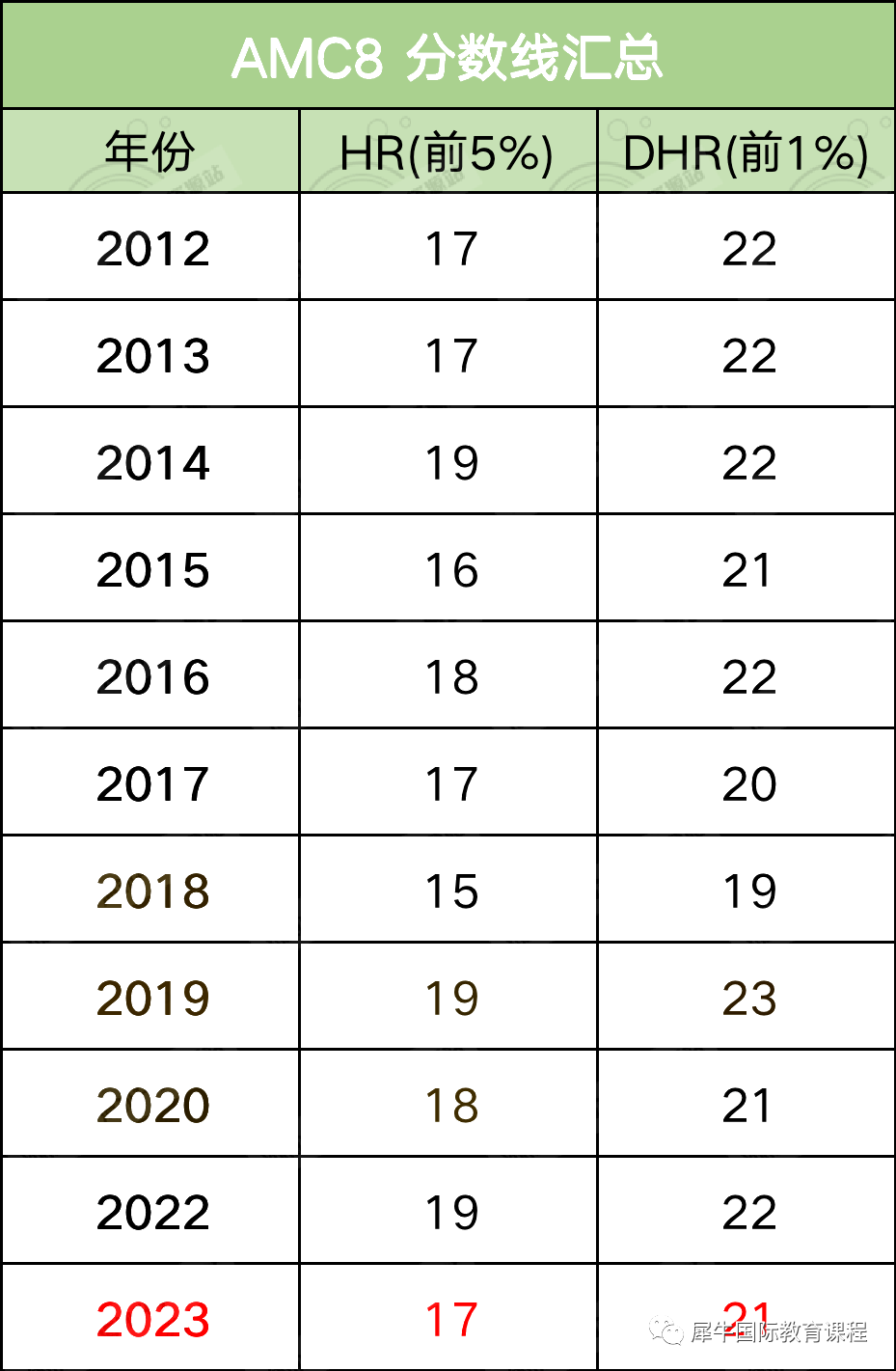
AMC10/12都会考察哪些知识点?
从知识点来说,AMC10/12有不少知识点是国内的高中或者国际课程覆盖的,然而,仍然有一部分内容需要同学们进行拓展。
2022年AMC10/12考情动态
01增加知识点不定方程的特殊形式佩尔方程(Pell)
去年的12A和10A都有点难度,想要拿130+的高分还是不容易的。特别是去年12和10的A卷都特别喜欢考不定方程,前年的A卷独爱函数和几何。
去年不定方程的这个考点,除了常规考察之外,增加了二元二次不定方程中的佩尔方程形式。
02函数中的最值问题考的比较灵活
常规的最值问题一共有6种方法:
1.利用函数单调性
2.基本不等式
3.划归为二次函数
4.化归为耐克函数或其他特殊函数
5.换元
6.数形结合等常用的6种方法,
对于复数的题目,AMC 12之前是很少考察最值问题的,在HMMT、PUMAC、BMT等S级比赛中,经常碰到复数的最值问题。
一般来说,复数的最值问题,都是用几何方法解决的,所以方法还是2个:
1.要么用几何图形画出来;
2.要么用代数式求出来。
03 对同余的考察偏向于灵活应用性考察
之前年份同余的题目,更偏向于同余方程7条基本规则的使用以及常规的基本例题题型,比如如下的题目:
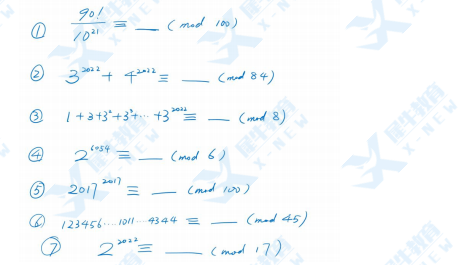
但是现在的题目则更倾向于应用性的考察(与数列、方程等结合在一起考察),这个难度显然比之前要大很多:
04考察对排列组合的考察:常规题型考察
对于排列组合—分类讨论、排列组合—操纵排列顺序都是常规题型考察,平常训练的比较多,这次考试没有新意,基本是老生常谈。
AMC10/12难题怎么快速找到思路?
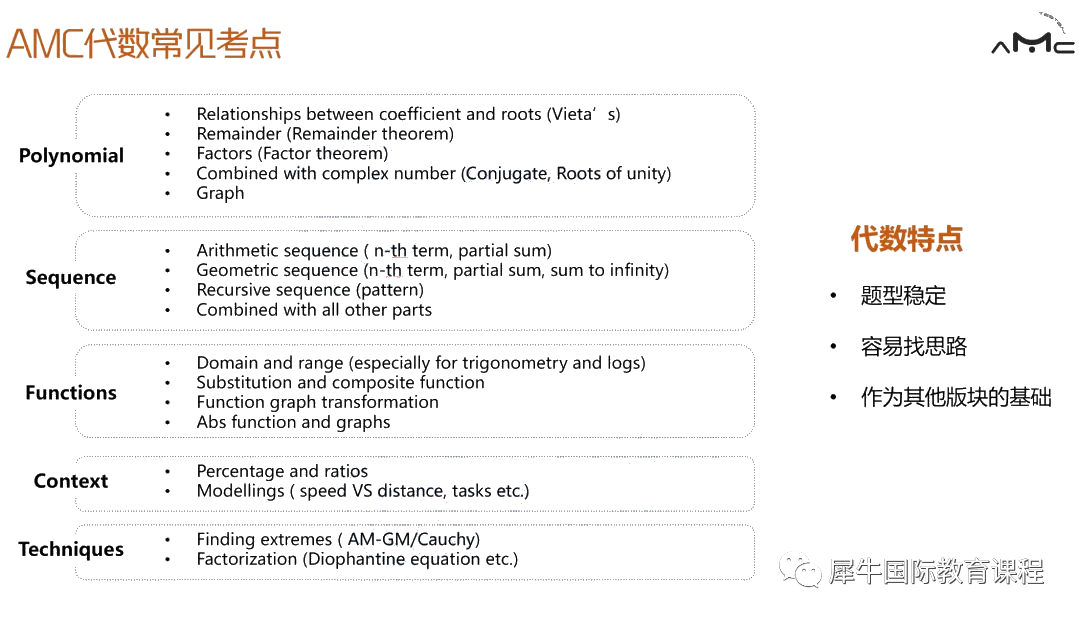
代数考察知识点
代数部分的常见考点主要集中在多项式,数列以及函数上。当然,也有很多应用题,主要分布在前面的1-10题。这类型题目需要建立方程,小心计算,千万不要因为粗心丢分哦!
而作为其他板块的基础,代数还需要大家掌握好求最大值和最小值的方法以及对复杂方程进行因式分解的能力。
值得大家注意的是,多项式中,高阶韦达定理是AMC的热门考点,大家一定要掌握。
几何考察知识点
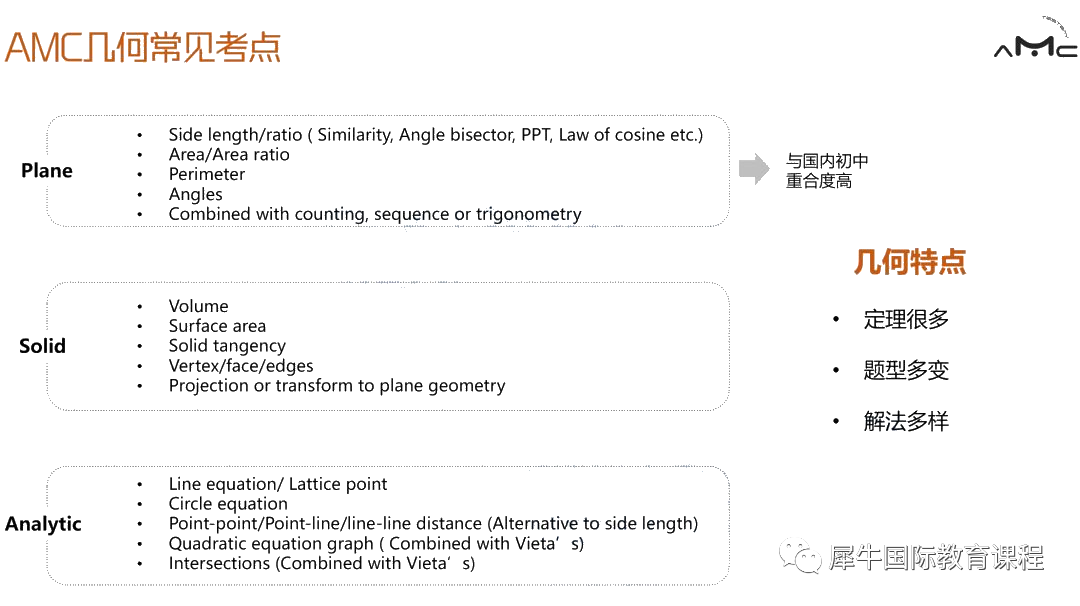
由于国内初中学习几何相对比较深入,大部分同学的几何基础比较扎实,面对AMC几何题时也比较得心应手。
同学们相对陌生的题型是立体几何转化为平面几何,这一内容需要同学们具备比较强的空间想象能力,多做多练勤脑补才是制胜关键。
另外同学们觉得比较棘手的问题则是立体图形的相切问题。
解决这类题型的关键就在于把立体图形转化为平面几何,并且利用切点推出各类与切点相关的性质,从而找到解题突破口。
数论考察知识点
数论题目在AMC10中占比有变大的趋势,所以掌握数论的题型和技巧是拿到高分的保障!
AMC的数论题型一般集中在整除与数位运算上。对于整除,我们常见的处理方法是质因数分解以及找出一些常用整数整除的规律。
例如能被3整除,5整除,9整除与11整除的数字有什么特点,进阶难度的题目需要同学们掌握模运算之后,能推算出被7整除或者任意整数的规律。
同时,模运算也能帮助你处理余数问题,不过略有挑战性,所以没有模运算概念的同学,抓紧时间学习吧!
另外,进制转换也是数论的一个考点哦,处理这类问题常用的方法就是将其他进制按number base的方法展开,观察规律。
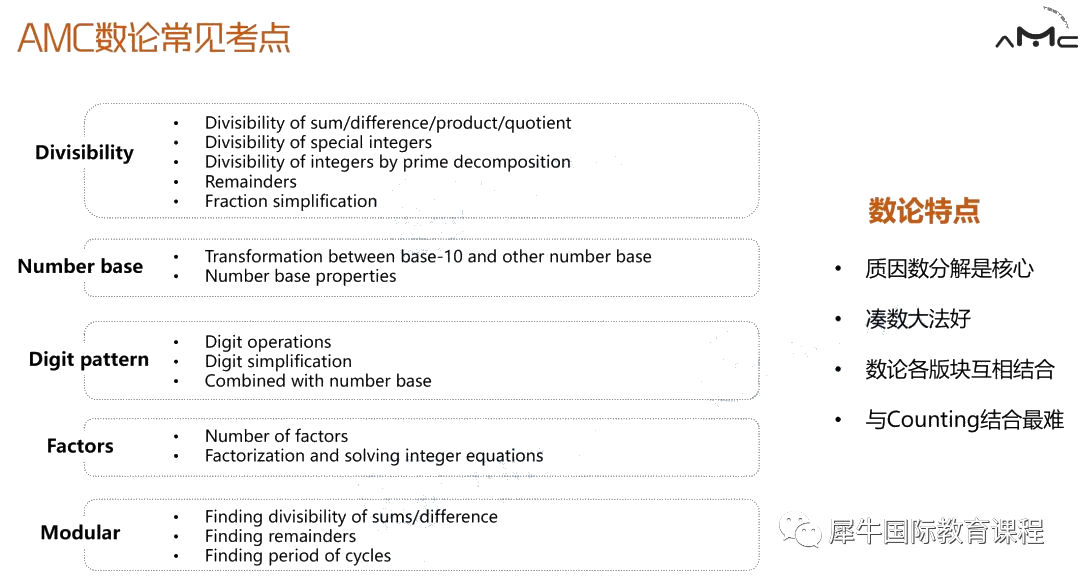
一般来说,单独考数论本身的题目并不难,难在数论题目经常与Counting结合,让你去数有多少个约数,多少个质数可能性或者概率等等,因此我们除了掌握数论板块题型与知识点的特点之外,还需掌握排列组合与概率的计算技巧与方法。
排列组合考察知识点
排列组合模块本身的知识点并不是很多,但是这个版块经常与各版块结合,瞬间能把题目难度拉上天。
而解决这类问题的技巧一般有两个:第一就是分类讨论,第二是遇到描述比较复杂的题目时,想办法举出正例和反例,观察他们的规律,再结合排列组合中的定理和公式求解。
在排列组合中,有一种与几何相结合的题型。这类型的题目突破口就在于找到临界条件,观察什么时候满足条件什么时候不满足条件,然后以临界条件作为等量关系找出概率。

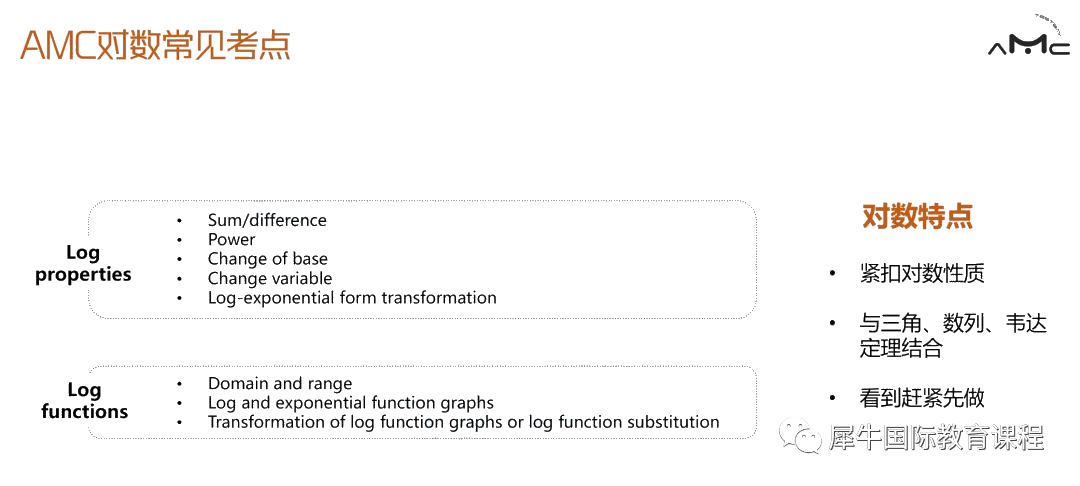
对数考察知识点
对数是AMC12的内容,不在AMC10的考察范围中。
相比而言,对数题目应该说是AMC12中最简单的题型,因为涉及的考点无非就两个:对数运算性质以及对数函数的性质。
绝大部分对数与其他版块结合的题目突破点就在于换底公式,根据方程特点确定对数的底进行运算即可。
在运算过程中,换元法使用频率很高,在没有思路的时候,不妨试试换元法吧!
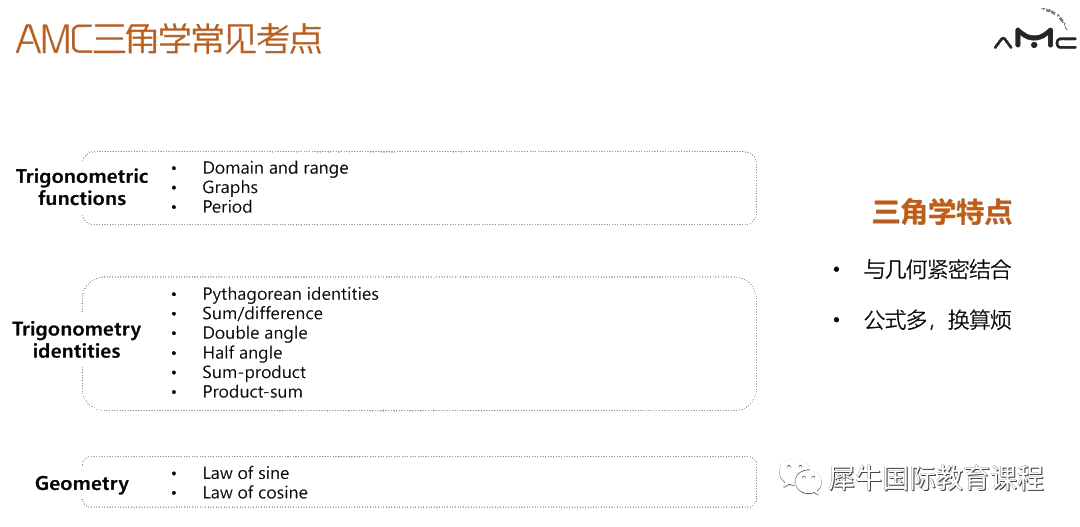
三角学考察知识点
AMC10不涉及三角学的内容,仅在AMC12中考察。
三角学其中一种重要题型就是求解三角恒等方程,另外就是使用正余弦定理以及三角恒等中的和角公式与倍角公式解决很多几何中涉及三角形的题目,所以AMC10的同学们注意了,虽然AMC10不直接考,但是积累三角学能帮助求解几何题目哦!
复数考察知识点
AMC12中复数本身的知识点和定理并不是很多,定理只有De Moiré’s theorem和Roots of unity,但是复数会与数列,三角函数,对数甚至是排列组合结合在一起,一年最多3题,甚至有些年份并没有出现复数的题目。
但是一旦有复数的题目,难度基本都是中上级别。
复数题型一般涉及两种,一种是复数的一般运算,这个时候通过转换复数的三种形式,结合题目条件做假设和计算;而另一种是涉及复数的次方运算,这个时候往往需要使用De Moiré’s theorem并结合三角函数来进行求解。
所以三角函数基础不够的同学,赶紧补上吧!!!
2023年AMC10/12考点预测
NO.1、AMC10/12 的必考知识点:
代数模块:基础运算、应用题(行程、逻辑、统计等)、多项式、数列问题与求和
几何模块:边长计算(勾股、相似等)、面积问题、立体几何
组合模块:基本计数与概率问题
数论模块:质因数分解与因数倍数问题
NO.2、AMC10/12大概率会考到的知识点:
代数模块:代数计算技巧(因式分解、换元、展开等)、二次函数与方程、绝对值和取整函数、数列和求和问题、直线与圆
几何模块:几何变换、圆地几何性质
数论模块:同余(剩余系、整除法则、同余方程)、整数方程、位值原理与进制
NO.3、AMC10/12有可能考和小概率考的知识点:
代数模块:多项式、不等式与极值问题
几何模块:角度计算、三角形的心
组合模块:进阶计数方法(递推、插板、PIE、1-1对应等)、无穷时间状态问题、组合极值与杂题、几何概率