美国AMC8介绍
美国数学竞赛AMC8(American Mathematics Competition 8)是一项面向初中生的数学竞赛,在美国广受欢迎。几乎所有的中学都会推荐学生参加。作为美国数学协会(MAA)主办的年度活动之一,AMC 8考试为全球学生提供了一个展示数学能力的机会。与AMC10和AMC12相比,是AMC美国数学竞赛中等级和难度最低的考试。
美国数学竞赛AMC8的备考学习对于之后参加AMC10/12学术活动至关重要,而AMC10/12是许多申请美国名校时需要填写的数学竞赛之一,其认可度非常高。因此,参加AMC8不仅是一次数学挑战,也是为未来在数学领域取得更高成就打下基础。
那么,接下来我们就详细介绍美国数学竞赛AMC 8考试的各个方面,帮助大家更好地了解这一数学赛事~
美国AMC 8-考试基本信息
报考条件:8年级(初二)及以下年级,参加活动时年龄不超过14.5周岁
考试时间:通常在每年的11月中旬进行。2024年的考试时间是1月19日。
报名方式:学生可通过学校或注册机构报名参加考试。报名截止时间通常为考试日期前的数周,因此及早获取相关信息并报名很重要。
考试时长:40分钟
考试形式:25道选择题。中国赛区提供中英双语试卷。
美国AMC 8-考纲及例题分析
美国数学竞赛AMC8考察知识点主要集中在基础代数、基础几何、基础数论、基础组合这四个模块。考点与7、8年级数学大纲相对应,包括(但不局限于)整数、分数、小数、百分数、比例、数论、日常的几何、面积、体积、概率及统计、逻辑推理等。
美国数学竞赛AMC 8从第1题到第25题难度是循序渐进的。
第1题-第10题:不会特别难,都是基础题目。
第15题-第20题:相应会有一些难度,但难度水平相当,只是考点有所不同。
第16-第20题:这五道题对学生来说非常重要,尤其是想要冲击前5%的学生。在这部分题目中,答对一道加1分,答错不扣分,所以学生需要注意答题策略,守住自己的分数。
下面我们就通过例题来更好的了解美国数学竞赛AMC8 考试难度吧!
美国数学竞赛AMC8例题解析
01、计算部分
主要涉及实际应用背景的问题,类似应用题,涉及分数、百分数、小数计算,但是复杂程度较低。考察学生的计算能力,因此,学生在答题时不能掉以轻心。
2017 Q5
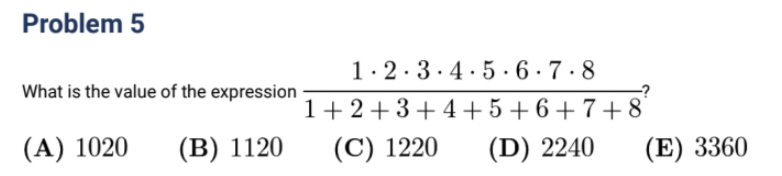
解析:分母求和,为36,可消去分子上的公约数2,3,6,再求分子的积,4x5x7x8 = 1120. 故选B。
02、代数部分
这部分涉及一次方程(组)的求解、开根号解二次方程、平面坐标系与直线方程、等差数列的通项与求和、简单等比数列、平方差公式与因式分解。近年来对于初中课内的代数内容考察越来越多,虽然难度不是特别大,但是大家还是要重视。
2018 Q5
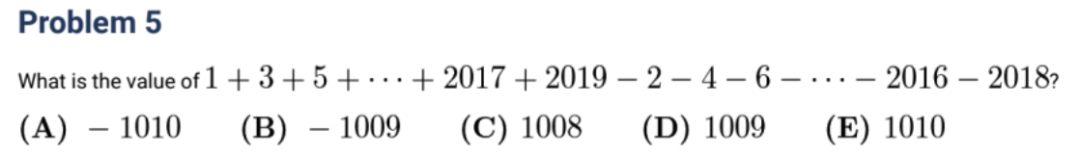
解析:这道题很明显将数字分为两组,前一组为正奇数,后一组为负偶数,每一组都是1010个,因此可以前后配对,1-2= -1,3-4= -1… 一共1010组,因此为-1010,故选E。
03、应用题部分
应用题是美国AMC8的考察核心,题目类型繁多,主要涉及分百比问题、行程问题等比率问题、图表类问题、统计量问题、逻辑推理问题、整数方程问题,以及列方程解问题的思想。
2019 Q10

解析:原先图表上周三为16人,人数最少,中位数是周一的20人。修改后周三为21,重新按大小排列后恰为第三个,即中位数增加1 人,排除A,C,E。平均数为总数除以5,由于多了5人,除以5后多1人,平均数+1,故选B。
04、几何部分
这部分涉及较多空间想象、圆与扇形、勾股定理等内容,这部分对于考生来说也是重难点,要熟悉常见平面图形的面积,周长公式和算法,还有求不规则图形面积的方法,包括拆分法、割补法等。考生年级对于圆或勾股定理等知识要多加巩固练习。
2018 Q20
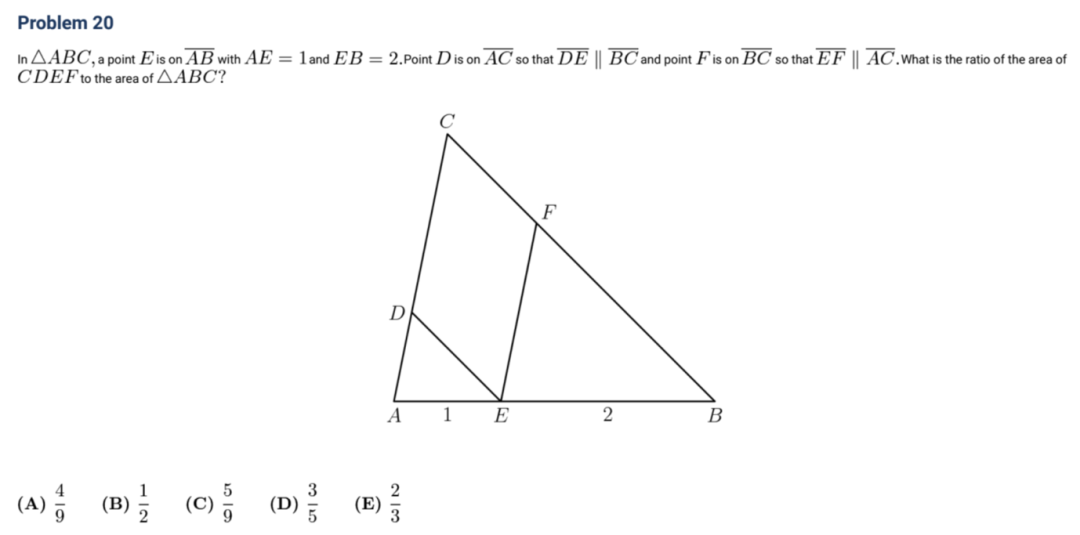
解析:这道题涉及三角形的比例关系。AE:AB=1:3,因此△ADE:△ABC=1:9。同理,△BEF:△ABC=4:9。因此,四边形AEFC面积:△ABC=5:9,由于△ADE面积为1/9的△ABC,CDEF面积为(5-1)/9的△ABC,4/9的△ABC,故选A。
05、计数部分
涉及较多的排列组合,容斥原理、加法原理、乘法原理等内容。其中计数原理要了解加法和乘法的区别,加法计数原理的关键词是分类,乘法中的关键词是分步。
2020 Q23

解析:3人分5个奖,排列组合问题。两种情况:1)有两个人各拿两个奖:2+2+1=5;2)有一个人拿了三个奖:3+1+1=5。针对第一种情况,学生1从5个奖中选2个,学生2从剩余3个奖中选2个,学生3得最后一个,用组合公式得30种。第二种情况:学生1从5个奖中选3个,学生2从剩余2个奖中选1个,学生3得最后一个,共20种。由于学生1,2,3有三种排列,(30+20)*3=150,故选B。
06、数论部分
涉及较为初步的质数与合数、约数与倍数、整除问题、余数问题,多次考察了位值原理。这部分内容对于考生来说有一定难度,数论部分中概念比较多,学生容易混淆,所以在复习的时候首先要弄清楚每部分内容的概念与性质和计算方法。
2018 Q18

解析:设这个数为x。当被6除时,余数为2。这意味着x+4是6的倍数。同理,当被9除时,余数为5。这意味着x+4是9的倍数。当被11除时,余数为7。这意味着x+4是11的倍数。接下来求6、9、11的最小公倍数(LCM):6 = 3*2,9 = 3*3,11 = 11*1。因此,LCM是3*3*2*11 = 198。所以,198+4 = 202 是所需的最小数字。满足给定条件的其他三位数是202+198*n,其中n=1,2,3,4。因此符合条件的所有三位数为202、400、598、796、994,共5个,故选E。
美国数学竞赛AMC 8-奖项设置
●全球卓越奖 Distinguished Honor Roll:全球排名前1%
●全球优秀奖 Honor Roll:全球排名前5%
●全球荣誉奖 Achievement Roll:6年级及以下在AMC 8中获得15分以上
好啦,今天的分享就到这里啦!希望对即将或准备报考美国数学竞赛AMC8考试的同学们有所帮助。