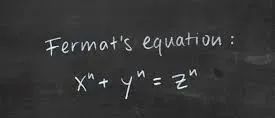本系列为大家带来基础代数数论的整理,最终会设计费马大定理一部分情形的证明,敬请期待
该系列的主要内容用英文编写,每篇文章会有中文的简介,帮助读者梳理思路,更好地完成阅读。所需要的知识主要为Galois理论和基础的交换代数,一些结论在第0节中分类整理,因此请读者先浏览第0节,如果有严重的知识漏洞可以考虑系统地学习。
如果读者想要系统地学习相关理论,可以参考一下书籍:
- Introduction to Commutative Algebra by M. F. Atiyah & I. G. MacDonald (1994)
- Algebra with Galois Theory by Emil Artin (2007)
- 基础拓扑学讲义 by 尤承业 (1997)
- Algebraic Number Theory by J.S. Milne (1998)
- Introduction to Cyclotomic Fields by Lawrence C. Washington (1997)
- Fermat's Last Theorem for Regular Primes by Keith Conrad
前两本为基础知识以供参考,这里写第三本主要是提供一个了解点集拓扑概念的渠道,实际上本系列中仅应用了欧式空间的拓扑,因此掌握一些分析知识就足够了。如果想要系统学习第一本可以学习第三本的点集拓扑部分。
第四本为本系列主要参考书籍,第五、六本为费马大定理的部分情况证明相关的知识。第六本为一篇论文,其中引用了第五本第五章的一个结论为引理,而该结论需要解析数论作为基础,因此本系列最终会直接使用该引理而不加证明。
本期文章包含三个小节:"Review of basic knowledge", "Ring of Integers","Discriminant",即“基础知识回顾”、“代数整数环”、“判别式”。
第0节“基础知识回顾”请读者自行阅览。
第1节“代数整数环”介绍了整的基本性质,环 在环 上整,如果 的元素均为 上的代数整数。一个重要的结论是整的传递性,即若 在 上整、 在 上整,那么 在 上整。一个环称为整闭的,如果其在分式域的整数闭包就是自身。可以证明 在 中的整数闭包是整闭的。
第2节“判别式”从线性代数出发定义了环扩张 中元素的迹和范数,进而定义了自由模环扩张的判别式。为了计算该判别式,引入了不可约多项式的判别式。最后,列举了两类不可约多项式的判别式的计算。判别式的作用会在下一节中提到,敬请期待。