困于AP微积分BC？得此图文可解！

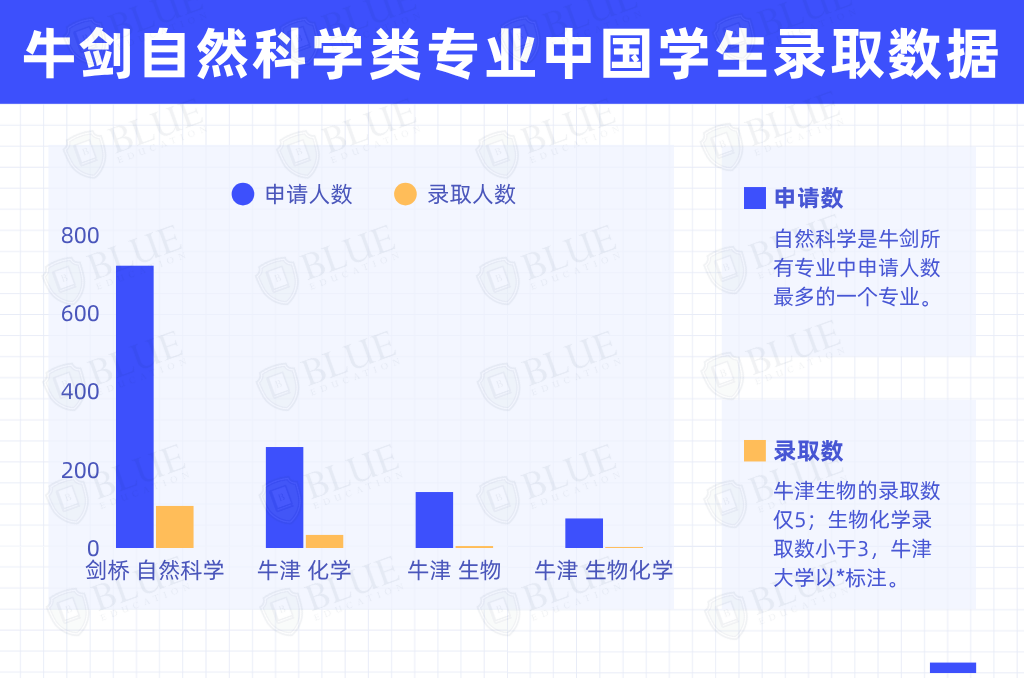
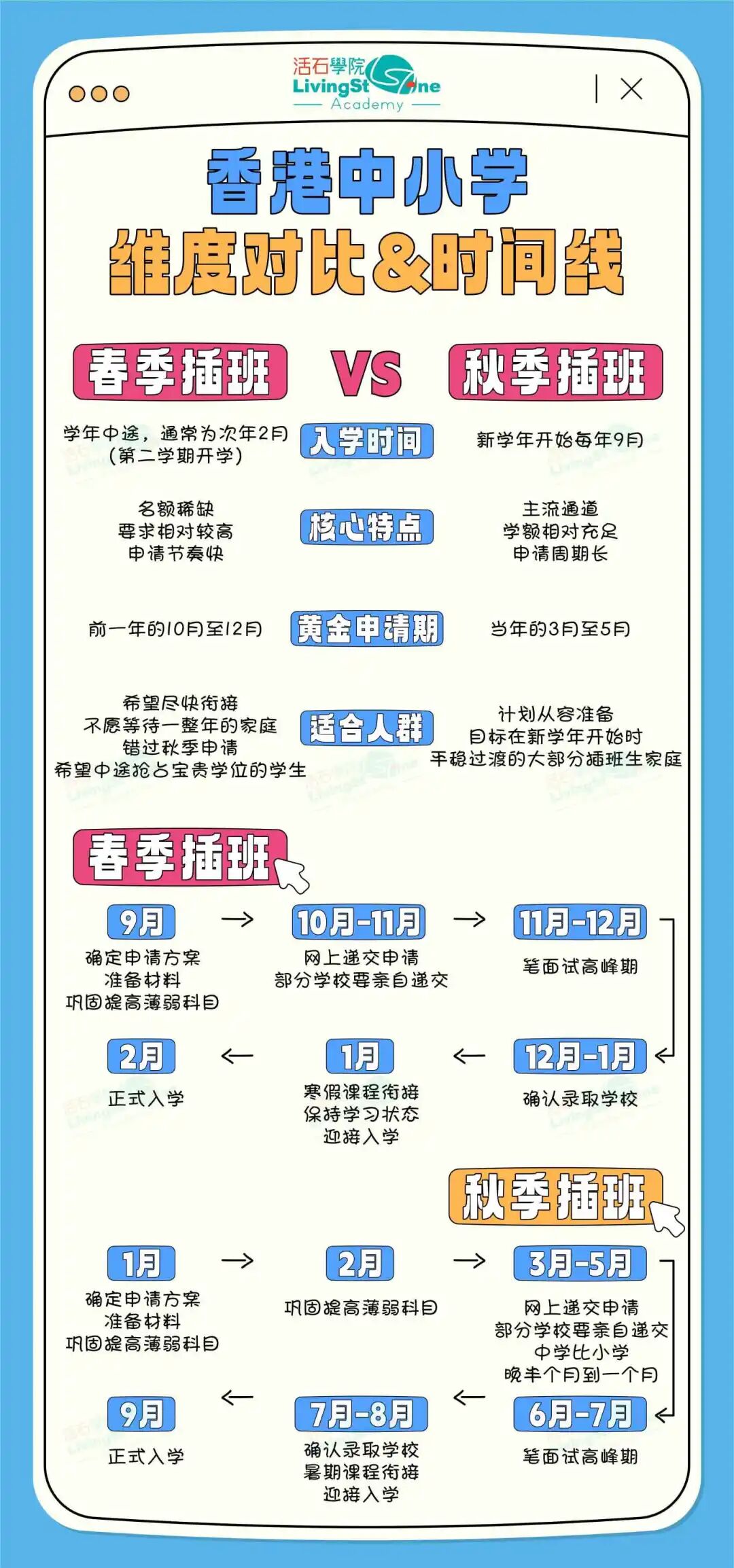
时不我待，国际学校AP报名最近正在有序组织中，同时也标志学校AP各学科的教学也正式从试水阶段进入常规化教学阶段。

作为进一步冲刺AP荣誉之路上“拦路虎”-AP微积分BC，对于升入国际班高二年级的学生无论是被动选择还是主动挑战的学生，最近的校内学习难度都在不断升温，如何在最需要打好基本功的阶段学好微积分BC，如下建议可以帮你有所作为！

起初高一你在AP预备微积分的学习上游刃有余，不曾想也就是过了个暑假，为何高二的AP微积分BC像是变了个天，突感不适难度增加。这里面的问题主要是数学认识主体从“形”的临摹到“魂”的交摄，抽象性的理解有大幅上升。

AP预备微积分学习的主体只要认识基本函数类型就行了，但是进入AP微积分后，考察主体需要同学们理解和应用好微积分的基本思想，这就不怪同学们有所吐槽偶有苦恼了。

那么，AP微积分BC既然已经躬身入局，如何破局解此困顿？不妨好好细品这张思维导图！

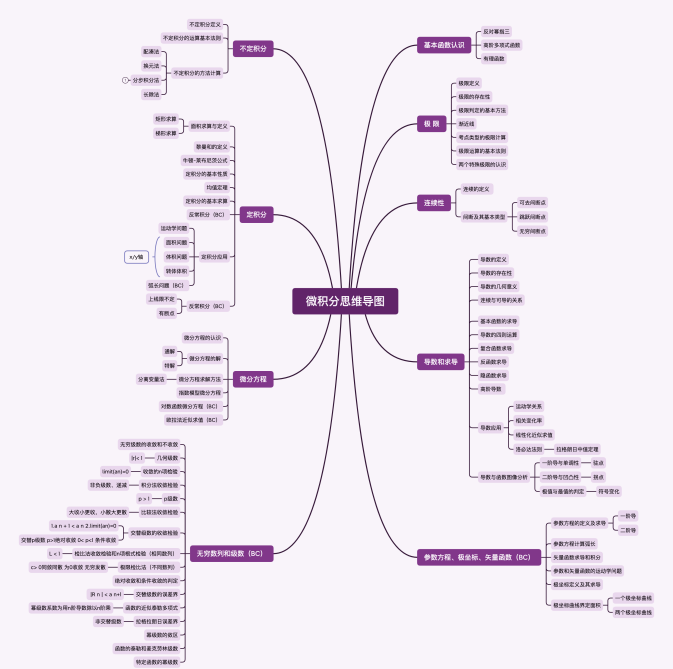
需要宏观上掌握的一些基本思想与理解：

1极限的思想，简单来说，极限就是一个动态逼近过程产生一个确定结果。极限的理解会贯穿于整个AP微积分BC的学习过程中，这也是为什么要把极限放在进入微积分学习主体学习的第一章，很多概念的定义和判定都与极限紧密联系。

2导数的定义，图像上就是某点处的切线斜率，应用题中表示瞬时变化率。导数的存在性可转化为极限的存在性去判定。

3积分的意义，不定积分表示的是求导后为同一个函数的一类函数，定积分表示由曲线和上下限所围成的封闭面积。

4反常积分的求解无论是趋于无穷的类型还是积分上下限中有断点的类型本质上都是转化为极限表达去计算。计算处准确数值则收敛，反之则发散。

5微分方程求解分离变量是关键，还原主体再求解。这部分需要重点注意一下对数模型的分析与变化，其次欧拉近似求解的关键是线性化近似求解的重复。

6级数部分看类型，特定条件判收敛。不同类型级数的收敛条件已经详细总结在思维导图上，注意把握重点。同时使用不同方法检验收敛时注意名称和用法。