在AMC12备考过程中,许多学生面临“知识盲区不明确、提分路径不清晰”的困境。本文将通过结构化知识图谱和分层提分策略,为不同水平的学生提供针对性指导。
1知识图谱:四大模块全面覆盖
AMC12的知识体系可以系统性地分为四大核心模块,每个模块包含若干重要子领域。以下是完整的知识结构图:
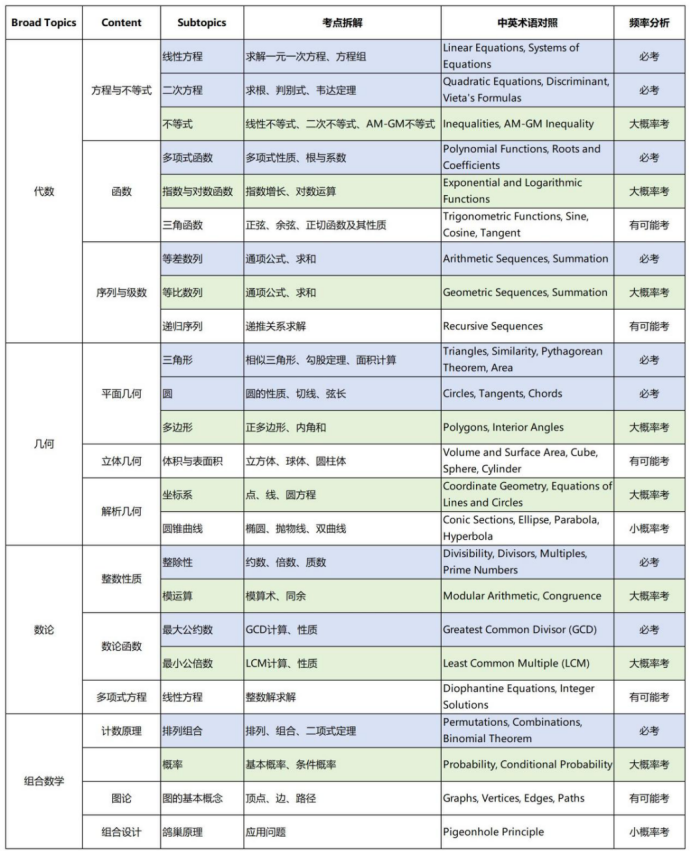
代数(约占40%)
作为AMC12的骨干模块,代数部分涵盖从基础运算到高级函数的完整体系:
- 基础运算:代数式化简、方程求解
- 函数与方程:多项式、指数函数、对数函数、三角函数
- 不等式:均值不等式、柯西不等式、绝对值不等式
- 复数:复平面、欧拉公式、蒂莫夫公式
几何(约占24%)
几何模块强调空间想象与逻辑推理:
- 平面几何:三角形、圆、四边形、相似与全等
- 立体几何:体积与表面积计算、空间几何体
- 解析几何:直线、圆、圆锥曲线的方程
组合数学(约占24%)
这一模块最考验逻辑思维:
- 排列组合:基本计数原理、排列数、组合数
- 概率:古典概率、条件概率、期望值
- 图论:基本概念、路径与回路
数论(约占12%)
数论题目往往难度较高:
- 整除与同余:最大公约数、最小公倍数、模运算
- 素数:素数判定、素数分布
- 数论函数:欧拉函数、莫比乌斯函数
AMC12的25道选择题遵循难度递进原则,可分为四个明显区间:
基础题(1-10题)
- 特征:题型以“数量关系、代数运算、基础几何”为主
- 目标:确保全部做对,拿到基础分数
- 备考重点:基本运算技巧、简单图形识别、勾股定理等基础知识点
核心题(11-20题)
- 特征:引入复杂代数技巧、组合计数、递推关系
- 目标:此区间是拉开分数差距的关键区域
- 备考重点:排列组合、函数变换、圆的基本性质等
拔高题(21-23题)
- 特征:多个知识点融合,解题路径不明显
- 目标:需要具备构造法、转化思想等竞赛技巧
- 备考重点:数论、高难计数题、函数建模等
挑战题(24-25题)
- 特征:达到或接近AIME水平,体现竞赛的“衔接台阶”
- 目标:冲击顶尖成绩的关键
- 备考重点:组合与概率极值问题、多变量不等式构造等
22024年真题分析与趋势洞察
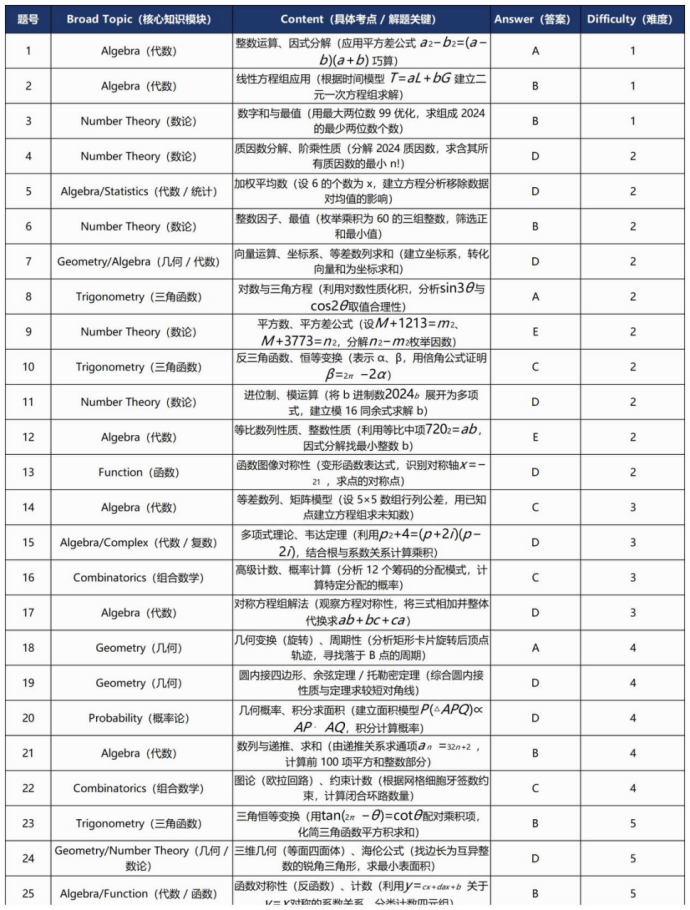
2024 年 AMC12(A 卷)解析图表,涵盖题号、核心知识模块、具体考点与解题关键、官方答案及难度分级,难度参考 AMC12 标准梯度(1 = 基础送分,5 = 极难 AIME 级),信息均来自 2024AMC12A 官方题目、答案及考点分析。
模块重点与命题趋势
1. 代数(核心拉分模块)
- 基础题(1-2 题):侧重整数运算(第 1 题平方差公式)、线性方程组建模(第 2 题时间模型)。
- 中档题(5、9、12、13 题):函数对称性(第 13 题指数函数对称轴)、等比数列整数性质(第 12 题求最小 b)、加权平均分析(第 5 题移除数据影响)。
- 难题(14、17、21、25 题):
- 矩阵等差数列(第 14 题 5×5 数组,需设公差联立方程);
- 对称方程组(第 17 题三式相加整体代换,求ab+bc+ca);
- 函数自对称(第 25 题分式函数关于y=x对称的系数关系,需分类计数)。
2. 数论(中档题集中)
- 高频考点:质因数分解(第 4 题求最小 n! 含 2024)、最值优化(第 3 题用 99 拆分 2024)、进制模运算(第 11 题 b 进制数被 16 整除)。
- 命题特点:弱化高阶定理(如费马小定理),强化枚举与同余分析(如第 6 题乘积 60 的整数和最值)。
3. 几何(难度分层明显)
- 基础题(第 7 题):坐标系向量求和,利用等差数列简化计算。
- 难题(18、19、24 题):
- 几何变换周期性(第 18 题矩形卡片旋转落于顶点 B 的周期);
- 圆内接四边形(第 19 题结合余弦定理与托勒密定理);
- 等面四面体(第 24 题整数边长锐角三角形最小表面积,需海伦公式)。
4. 三角函数(创新考法)
- 中档题(8、10 题):对数与三角方程定义域分析(第 8 题log(sin3θ)+log(cos2θ)=0);反三角函数恒等变换(第 10 题 3-4-5 与 7-24-25 三角形角度关系)。
- 极难题(23 题):利用tan(2π−θ)=cotθ配对化简平方积求和,需三角恒等变形技巧。
5. 组合 / 概率(重逻辑轻计算)
- 组合计数(16 题):筹码分配特定模式概率,需分析玩家角色分配(红、白、蓝筹码归属)。
- 几何概率(20 题):等边三角形内随机点面积概率,积分计算AP⋅AQ<21的区域。
32026年考试形式重要变化
需要特别注意的是,从2026年开始,AMC10/12将全面取消线上考试,全球考生强制回归线下纸质考场。这一变化要求考生提前适应纸质答题方式,特别注意书写规范和答题卡填涂训练。














