克拉默法则 (Cramer’s Rule)是线性代数中一个非常经典的定理。它提供了一种只用
系数的行列式就能把方程组的解写出来的公式,最近看到有些同学使用过今天就来介
绍一下。
基础演示:解决 2 × 2 线性方程组
对于简单的低阶方程组,克拉默法则逻辑非常清晰。我们来看这个例子:

为什么工程上很少用它?
既然公式这么整齐,为什么计算机解大型方程组(比如天气预报、结构力学中动辄上万个未知数)时不用它?
原因:计算量爆炸。
真正的价值:理论推导与微分几何
克拉默法则真正的舞台不在于“算出数字”,而在于“表达关系”。在数学分析和微分几何中,我们需要证明某个解存在,或者推导解的解析式,此时克拉默法则无可替代。
拓展:隐函数求导(你们以后会学到的,先了解一下)
在微分几何中,我们经常遇到由方程定义的曲线或曲面,无法直接写出 y = f(x),但我们需要求切线或变化率。

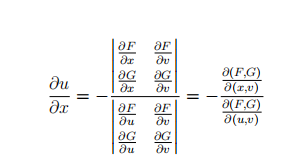
结论:上面这个用雅可比行列式(Jacobian)表达的公式,是微分几何中坐标变换和切空间计算的核心工具。如果没有克拉默法则,这类理论推导将变得异常繁琐且难以形式化。
所以,克拉默法则不是为了算数的,它是为了写公式的。