平面几何的三角方法：正弦定理

在上一篇文章《平面几何与图形的逻辑美》里，我主要介绍和讨论的是纯几何方法。同时，我也在文末概述了解析几何解法的思路。

事实上，解决几何问题，除了纯几何方法和解析几何，还有第三个工具——三角方法。上文中也有留言指出，文中所讨论的问题就可以用三角方法求解。

三角方法的核心是三角函数——通过三角函数建立长度和角度之间的关系。三角方法无需建立坐标系，所以不属于解析几何。

平面几何和解析几何各自都有一套系统的概念，并且建立了庞大的公式和定理库。相对而言，三角方法的奠基概念就是几个三角函数，公式的数量也不多。

三角方法的这种“先天不足”，使得它不能像前两种方法那样，成为通用型的几何方法。

三角方法中两个常用的重要公式是正弦定理和余弦定理，本文将讨论前者。正弦定理刻划了三角形的三边和三角的关联性，并且形式很对称，是一个优美的公式，如下图。

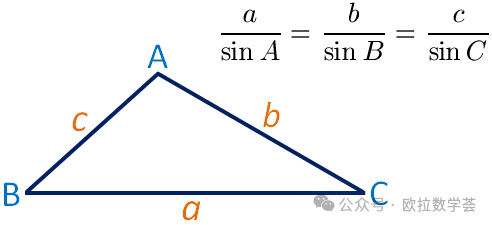
通常在表述正弦定理时，不会写出这三个相等的比值的意义。事实上，这个公共值恰好是三角形的外接圆直径。为了证明这个性质，我们考虑圆O内任一条弦AB，如下图。

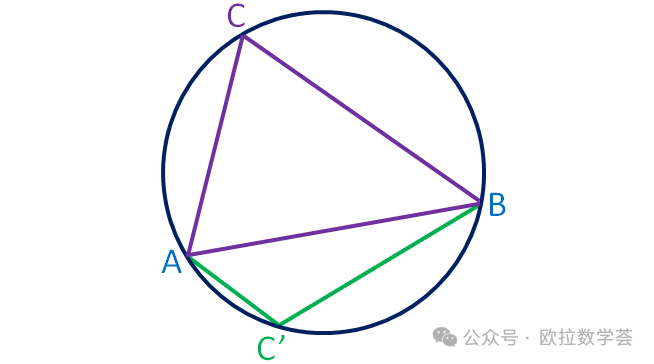
在圆周上另外任取一点C，然后连接AC和BC。我们下面证明

AB/sin∠ACB=2R.

注意到弦AB把整个圆周分割为两段圆弧。当点C在同一段圆弧的不同位置取时，所得的∠ACB的角度都相等；然而，在两段圆弧上取点C所得的∠ACB的角度并不相等。事实上，上图中的∠ACB和∠AC'B互补，即

∠ACB+∠AC'B=180°.

由正弦函数的性质，互补的角的正弦值相等，即

sin∠ACB=sin∠AC'B.所以我们可以不妨设∠ACB≤90°。

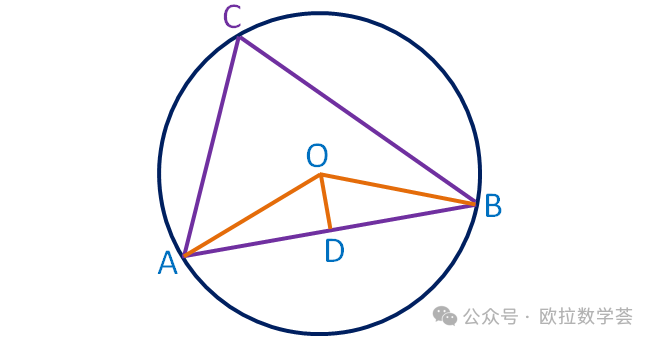
连接AO和BO，则∠AOB=2∠ACB（同一条弦所对的圆周角是圆心角的两倍）。过O作AB的垂线交AB于点D。由于AO=BO，所以OD平分边AB和角∠AOB。再由正弦函数定义，

sin∠AOD=AD/AO.而AD=AB/2，AO=R。所以sin∠AOD=AB/(2R),另一方面，∠AOB=2∠AOD，所以∠ACB=2∠AOD，从而sin∠ACB=AB/(2R).

我们把上面的结论完整表述如下：设AB为圆的任意一条弦，C为圆周上不同于A，B的另一点，则AB/sin∠ACB=2R，其中R为圆的半径。

注意到，对任意三角形和它的外接圆，三角形的任一条边和它的对角正好对应上面命题中的弦AB和∠ACB。由此即可推出正弦定理。

现在回到《平面几何与图形的逻辑美》一文中的问题。由于正弦定理建立了三角形的边、角和其外接圆直径的关联性，因此我们无需作出直径，而只要计算三角形的某一条边和其对角的正弦值的比。

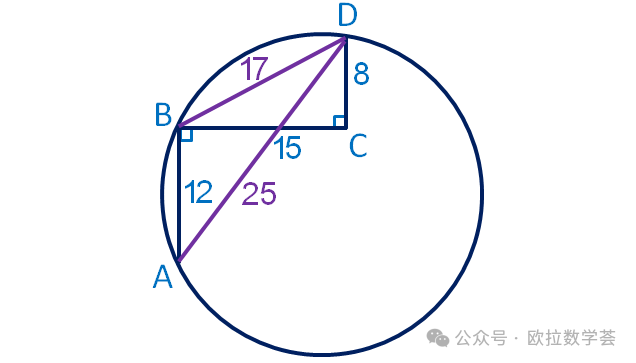
如上图，连接AD和BD，则△ABD是圆的内接三角形。利用勾股定理不难求出BD=17，AD=25。根据已知条件，△ABD的三个内角中，相对容易计算正弦值的是∠ABD。

由于∠ABD和∠BDC互补，所以sin∠ABD=sin∠BDC。而sin∠BDC=15/17，因此

2R=AD/sin∠ABD=85/3.

不难发现，当AB, BC, CD的长度取其他（合理的）数值时，上面的解法仍然适用。也就是说，前文中对这个问题推广后的一般问题。

最后做一个简单的小结。

在这个几何问题上，三种方法都发挥了它们应有的效力，解答过程都很简洁。

平面几何（以及延伸出来的立体几何）是解决几何问题的经典工具，处理以多边形和圆为代表的基本几何图形的能力很强，并且展现出独特的艺术性和美感。

然而，当人们的关注点开始转向更复杂的几何形状，例如螺旋线、二次曲线时，纯几何方法就变得捉襟见肘了，即使用上很多高难度技巧，也只能处理一些相对简单的情形。

解析几何是用代数工具系统性地解决几何问题的方案，其基本思想是建立直角坐标系，把几何对象和几何关系转换为关于坐标的代数表达。

这种革命性的思想成功地突破了纯几何方法的瓶颈。并且，随着代数方法本身的不断发展壮大，也为拓展和丰富解析几何的理论提供了强大的动力。

三角方法，如前文所述，并非通用的几何工具。但对于特定条件的问题可以提供有别于前两种方法的独特思路。

三角函数作为一类特殊函数，本身可以建立起一套独立的理论，并与数学的其他理论体系相结合。几何学的三角方法就是一个典型的例子。此外，函数论中著名的傅里叶分析，也是在三角函数系上搭建起来的一个庞大的理论架构。