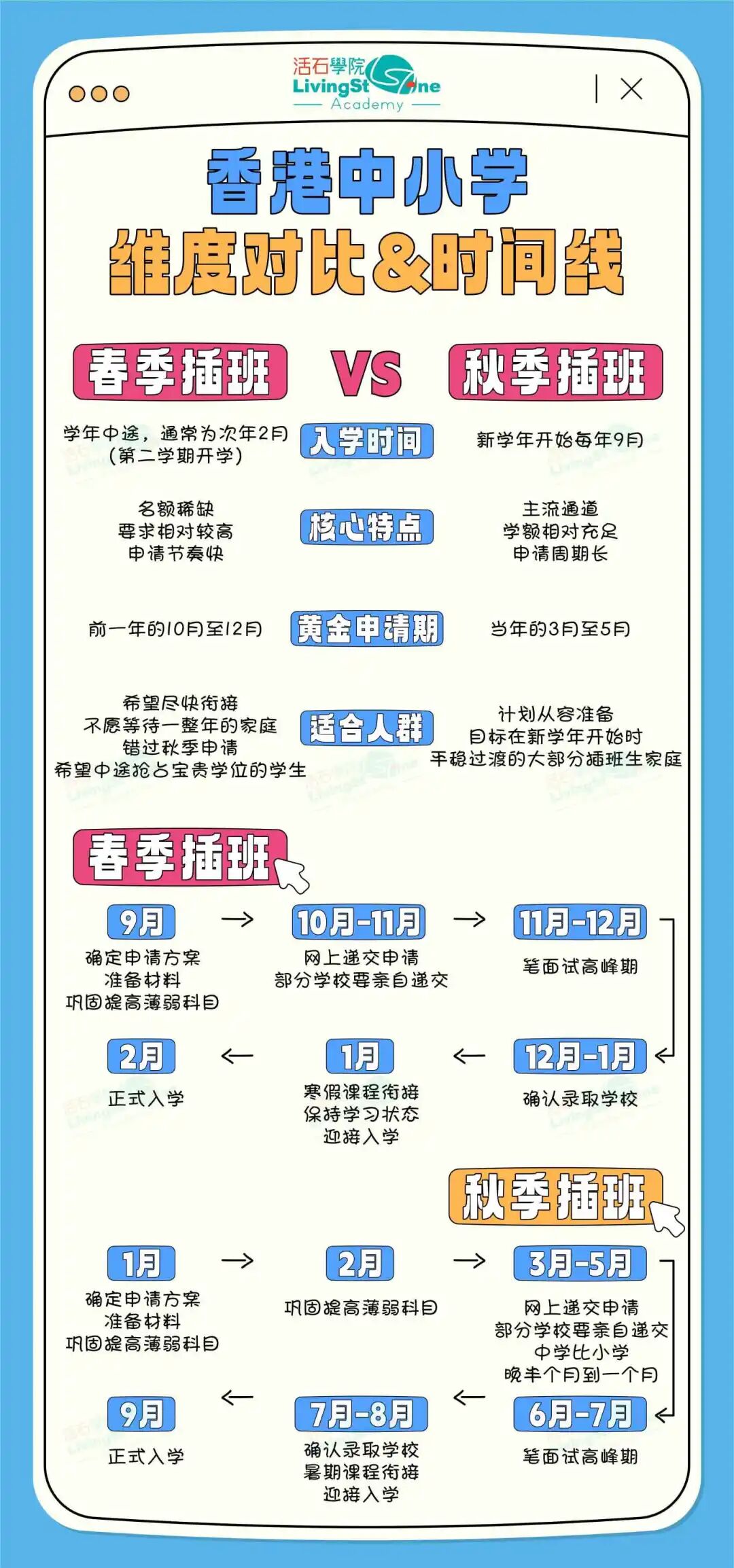
一、导师简介

在香港中文大学(深圳)(CUHK-Shenzhen)的学术体系中,Qihui CHEN教授是管理学院与深圳高等金融研究院(SFI)的重要学术骨干。对于计划攻读计量经济学方向博士学位的学生而言,其学术背景、研究方向与教学经验均具有显著的指导意义。
1.1 教育背景
教授的教育路径不仅跨越国内外顶尖院校,更构建了“数学+经济”的跨学科知识体系——这一背景对计量经济学研究至关重要,因为计量方法的创新既需要数学理论支撑,又需结合经济问题的实际场景:
-2017年,正是在加州大学圣地亚哥分校(University of California, San Diego),Qihui CHEN完成了经济学博士阶段的学习,并获得博士学位(PhD in Economics);
-博士之前,他的学习经历分为两阶段:本科阶段于厦门大学(Xiamen University)同时拿下经济学学士(BA in Economics)与数学学士(BSc in Mathematics);硕士阶段则先后在厦门大学和新加坡管理大学(Singapore Management University)攻读经济学,最终获得两个经济学硕士学位(MA in Economics、MSc in Economics)。
1.2 学术职位与教学领域
目前,教授身兼数职,既深耕教学与研究,也参与学术管理,这意味着博士研究生可能获得多维度的学术支持:
-在深圳高等金融研究院(SFI),他担任副教授(Associate Professor)与SFI研究员(SFI Fellow),深度参与研究院的学术研究与交流;
-同时,他还负责深圳高等金融研究院经济学硕士项目(MSc Programme in Economics)的管理工作,担任项目主任(Director),对经济学人才培养体系有深刻理解;
-教学上,他的授课领域集中于经济学(Economics),尤其擅长计量经济学相关课程,能帮助博士研究生搭建从理论到应用的完整知识框架。
1.3 核心研究方向
教授的研究始终围绕计量经济学的两大核心领域,且理论与应用并重,这一特点能为博士研究生提供“理论创新+实践落地”的双重训练:
-其一为计量经济学理论(Econometric Theory),重点研究统计推断方法的创新,例如如何解决模型识别难题、如何优化估计量的统计性质等;
-其二为应用计量经济学(Applied Econometrics),核心是将理论层面的计量方法应用于实际经济问题,比如面板数据建模、政策效果的量化评估等。
二、近期文章和项目解析
教授的学术成果集中发表于计量经济学领域的权威期刊,每篇文章均针对该领域的关键技术痛点提出解决方案;同时,结合他所在机构的研究特色,我们也能梳理出其潜在的研究项目方向,这些信息对博士研究生选择研究课题具有重要参考价值。
2.1 期刊与文章核心价值解析
教授发表的期刊均为计量经济学领域的“硬通货”,其成果的价值可从“期刊影响力+研究解决的实际问题”两方面解读:
1. “Robust and Optimal Estimation for Partially Linear IV Models with Partial Identification”(Journal of Econometrics, Accepted)
- 先看期刊:Journal of Econometrics是计量经济学领域的顶刊,仅接收理论严谨、方法创新的研究,能被该刊接收,本身就说明成果的学术高度;
- 再看贡献:文章要解决的是“部分线性工具变量模型(Partially Linear IV Models)”的“部分识别(Partial Identification)”问题——这类模型在分析存在遗漏变量、测量误差的数据时常用,但传统估计方法在模型识别不充分时容易出现偏差。教授提出的新方法同时满足“稳健性(Robust)”与“最优性(Optimal)”,为实际数据的可靠分析提供了新工具。
2. “Inference on Functionals under First Order Degeneracy”(with Zheng Fang, Journal of Econometrics, Vol. 210(2), pp.459-481, 2019)
-这篇文章同样发表于Journal of Econometrics,聚焦的是“一阶退化(First Order Degeneracy)”场景下的“泛函推断(Inference on Functionals)”。简单来说,当模型的核心参数满足退化条件(比如方差趋近于0)时,传统方法无法对经济指标(如弹性、边际效应)进行有效推断。教授与合作者通过改进统计量构造,填补了这一理论空白。
3. “Improved Inference on the Rank of a Matrix”(with Zheng Fang, Quantitative Economics, 2019)
-期刊方面,Quantitative Economics是计量经济学领域的一流期刊,以“理论与应用结合紧密”著称;
-研究价值在于:矩阵秩(Rank of a Matrix)是很多计量模型(如因子模型)设定的关键——因子个数其实就是矩阵的秩。但传统的秩推断方法在样本量较小时精度不足,教授的改进方法提升了推断准确性,为因子分析、面板数据降维等应用提供了更可靠的依据。
4. “Improvement in Finite-Sample Properties of GMM-Based Wald Tests”(with Yu Ren, Computational Statistics, Vol. 28(2), pp.735-749, 2013)
-Computational Statistics是计算统计学领域的核心期刊,专注于统计方法的数值实现与性质优化;
-文章解决的是GMM方法的痛点:广义矩估计(GMM)是计量中常用的方法,但基于GMM的Wald检验在样本量较小时(如微观调查数据)常出现“过度拒绝”或“功效不足”的问题。教授通过调整检验统计量的权重矩阵,显著改善了Wald检验的有限样本性质,让小样本数据的推断更可靠。
5. “Testing Homogeneity in Panel Data Models with Interactive Fixed Effects”(with Liangjun Su, Econometric Theory, Vol. 29(6), pp.1079-1135, 2013)
-Econometric Theory是计量经济学理论领域的权威期刊,专门发表基础理论创新成果;
-研究意义在于:有交互固定效应的面板数据模型能同时考虑个体差异与时间效应,但模型是否适用,取决于“同质性(Homogeneity)”——即核心参数是否在所有个体间一致。传统检验方法在交互固定效应下会失效,教授提出的新方法恰好解决了这一问题,为面板数据模型的合理设定提供了判断标准。
2.2 潜在研究项目方向
结合教授的研究成果与深圳高等金融研究院“金融+计量”的交叉定位,我们可以推断出他当前或未来可能参与的研究项目,这些项目也可能成为博士研究生的课题方向:
- 金融计量应用类项目:比如将模型识别、推断方法创新应用于金融数据——像利用高频数据分析数字货币的价格波动,或通过文本数据(如企业年报)提取信息,构建金融风险度量指标;
- 政策评估类项目:这类项目通常与政府或企业合作,核心是用计量方法评估政策效果——例如用面板数据模型、工具变量方法分析产业补贴政策对企业创新的影响,为政策调整提供量化依据;
- 计量方法优化类项目:针对实际场景中常见的复杂数据(如高维数据、缺失数据),开发新的估计与推断工具,让计量理论能更好地落地到实际问题中。
三、未来研究预测
从教授现有的研究脉络来看,其未来的研究方向会紧密结合计量经济学领域的发展趋势,既延续自身的理论优势,又关注实际应用需求。以下四个方向具有较高的可能性,且对博士研究生的课题选择具有参考意义:
3.1 复杂数据下的计量方法创新
现在的研究越来越多地面临高维数据(比如包含几百个解释变量的微观数据)、非结构化数据(比如金融新闻文本、企业社交媒体数据),传统计量方法在处理这些数据时会遇到“维度灾难”“模型难以识别”等问题。教授在计量理论方面有深厚积累,未来很可能会往这个方向探索——比如开发适用于高维部分线性模型的估计方法,或把机器学习中的变量选择技术(如LASSO)与计量中的工具变量方法结合,解决复杂数据的推断难题。
3.2 金融计量的深度应用
深圳高等金融研究院的核心定位是金融领域的研究与人才培养,教授的计量方法创新大概率会进一步向金融场景延伸:一方面,可能会研究数字货币、绿色金融等新兴领域的计量建模——比如用高频数据估计加密货币之间的波动溢出效应;另一方面,可能会优化金融风险度量工具——比如改进VaR(风险价值)的估计方法,帮助金融机构更准确地管控风险。
3.3 政策评估计量的拓展
现在政策制定越来越强调“量化依据”,政策评估计量因此成为热门方向。教授未来可能会在“因果识别”上做更深的研究——比如针对环境政策、产业补贴政策,开发更精准的双重差分(DID)、合成控制法(SCM)改进方法,解决传统评估中“选择性偏误”“政策内生性”等问题,让政策效果的评估更科学、更可靠。
3.4 部分识别与稳健推断的深化
教授最新被Journal of Econometrics接收的文章聚焦“部分识别”,而这正是当前计量经济学的研究热点。未来,他可能会把部分识别的应用场景进一步拓展——比如在劳动经济学(估计教育回报率)、产业组织(测度市场势力)中,分析模型部分识别时能得出哪些政策启示;同时,可能会把“稳健推断”与机器学习结合,开发出对数据分布、模型设定不敏感的推断方法,让计量结果更稳健、更可信。